feature
That’s How the Kangaroo Bounces
A Biological Case Study to Teach Energy Concepts
Journal of College Science Teaching—September/October 2022 (Volume 52, Issue 1)
By Erin M. Craig, Sydney Galbreath, Timothy Sorey, and Derek Ricketson
A growing number of Introductory Physics for Life Sciences courses have been developed to prepare biology, premedicine, and pre-health majors for cross-disciplinary connections between physical principles and biological systems. Many students find it challenging to apply idealized algebra-based general physics to more complex biological systems. A novel biological case study was developed to teach undergraduates to expand their energy transformation analysis of a simple system—a bouncing ball—to a more complex biological system of a kangaroo hopping. Similar to a ball, kangaroos transform elastic potential energy into kinetic energy to power their “bouncing.” Unlike the bouncing ball, kangaroos gain additional potential energy through metabolic processes. Students follow a sequence of guided tutorials that facilitate small-group learning as they evaluate quantitative data from video analysis with metabolic energy expenditures from literature to synthesize a real-world understanding of energy transformations. In this article, we describe learning progressions, practical tips for teaching, and lessons learned in this activity covering energy transformations.
Living organisms rely on energy transformations to perform vital processes, but the inherent complexity of biological systems often makes it difficult for students to describe the flow of energy in a particular organism, even once they have an accurate understanding of the relevant energy concepts (Opitz et al., 2017). Physics concepts are often introduced in the classroom using minimal models—such as the proverbial “spherical cow”—in order to distill the fundamental principles in a tractable framework. While this approach is effective for building basic comprehension of physical principles, many students lack the ability to transfer their physics content knowledge to more complex situations (National Research Council, 2002). A growing number of Introductory Physics for Life Science (IPLS) university courses have been developed or adapted in recent years with the goal of better preparing life science majors to make cross-disciplinary connections between physical principles and biological applications (Meredith & Redish, 2013). Meeting this challenge requires curriculum that does not simply graft biological examples onto traditional physics content as an afterthought, but instead provides students with the experience of using physics to gain a richer understanding of a multifaceted biological system. Physics education research (PER) suggests that context-rich case studies are effective tools to teach critical thinking by challenging students to grapple with the “messy” process of actual science (Herreid, 2004). With the goal of helping students develop a more sophisticated understanding of energy transformations in real-life situations, we developed a case study approach for students to investigate the mechanical energy transformations that take place during kangaroo-hopping locomotion.
Red kangaroos have a remarkable ability to store large amounts of elastic potential energy in their tendons, allowing them to hop quickly over long distances while expending minimal metabolic energy (Kram & Dawson, 1998; Webster & Dawson, 2004). We developed a sequence of guided tutorials in which students work in small groups to analyze the energetics of kangaroo locomotion using a simpler nonbiological system—a bouncing ball—as a baseline for comparison. Using video analysis software and metabolic energy expenditures from literature, students quantify movement to draw conclusions about the forms of energy involved throughout a kangaroo’s motion. We implemented this set of lessons in an algebra-based IPLS undergraduate course over three 80-minute class periods, in which group work was punctuated by brief instructor-led class discussions. We also adapted and taught these lessons in an interdisciplinary general education course within our university’s honors college. We expect that the kangaroo locomotion case study would also be suitable for high school physics courses, as it provides a uniquely interdisciplinary approach to teaching energy conservation principles. We provide an up-to-date addendum that aligns this lesson with the Next Generation Science Standards (Online Appendix 1).
Procedure
Day 1: Bouncing ball video analysis
We began with a classic lab in which students use video analysis to investigate the motion of a bouncing ball (Stoeckel, 2018). Students worked in groups of three or four to make initial predictions that addressed the following questions:
- What forms of mechanical energy does a bouncing ball have throughout its motion?
- When does the ball exchange energy with its environment?
Most students correctly predicted that the ball loses energy to the environment every time it contacts the ground, and many lab groups also quickly grasped that the ball lost gravitational potential energy when falling and gained gravitational potential energy when moving upward. However, many students were unable to predict how kinetic energy would change throughout the ball’s motion.
Students tested their predictions by analyzing a movie of a tennis ball being dropped from a height of 1 meter, using an Open Source Physics Java tool called Tracker (Figure 1A; see also Brown, 2019). Frame-by-frame data were obtained from the video, producing graphs of position versus time and velocity versus time (Figure 1A and 1B; Supplemental Movie in Online Appendix 2). Gravitational potential energy (PEg = mgh), kinetic energy (KE = ½ mv2), and total mechanical energy (PEg + KE) for each time point were then calculated in Excel, referencing the corresponding vertical position and velocity values (Figure 1C). By examining the plots of energy versus time (Figure 1C), students were able to make two key observations: (a) When the ball is off the ground, there is a trade-off between kinetic energy and gravitational potential energy. As one increases, the other decreases, and vice versa, while the total mechanical energy remains relatively constant during each ball bounce. (b) The total mechanical energy diminishes for each successive ball bounce.
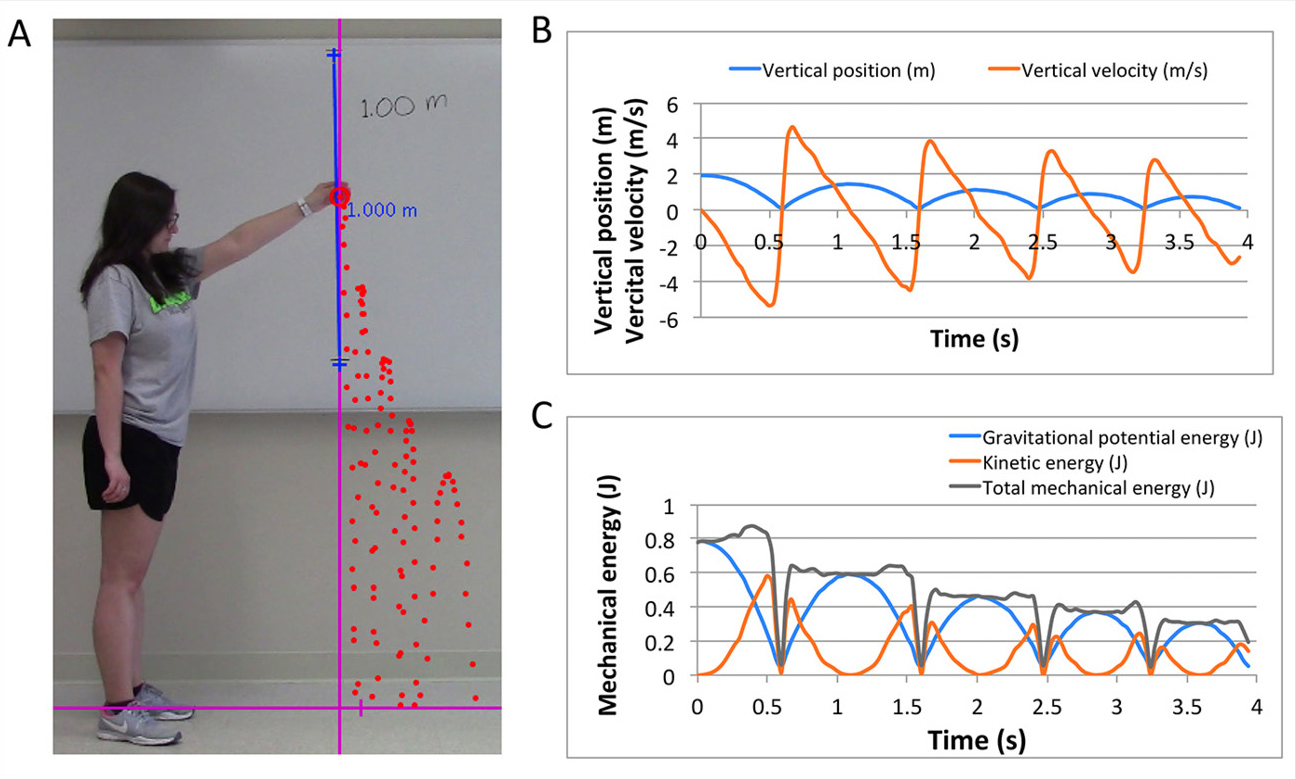
Case study Day 1: Video analysis of the motion of a bouncing ball.
Note. (A) Screenshot of bouncing ball video in the Tracker video analysis platform used in the class. (B) Sample student data tracking the vertical position and vertical velocity of the center of mass of a bouncing ball as a function of time. (C) Sample student calculations of gravitational potential energy, kinetic energy, and total mechanical energy corresponding to the motion data in part B. The video used for this activity is provided in Online Appendix 2.
Student groups were asked to brainstorm explanations for where the energy went, and they suggested a variety of reasonable explanations, including heat transfer to the ground and generation of sound waves.
Day 2: Kangaroo video analysis
On the second day, we invited students to consider how the mechanical energy concepts discussed the previous day might apply to kangaroo hopping. We showed the class a video of a red kangaroo hopping over level terrain, which we recorded with permission at the Outback Kangaroo Farm: Wildlife Park in Arlington, Washington (Figure 2A; Supplemental Movie in Online Appendix 3). During a think-pair-share discussion, students noted similarities and differences between the bouncing ball and the kangaroo. Students suggested several likely “complications” inherent to the kangaroo’s motion, noting that the kangaroo has more moving parts and internal structure than a ball, and unlike a ball, a kangaroo gets energy from consuming food.
Students performed similar analyses on kangaroo hopping as they did for the bouncing ball the previous day, recording vertical position and velocity and using these to calculate mechanical energy for three or four hopping cycles (Figure 2B and 2C; Table 1). As we circulated the room, we observed groups discussing the pros and cons of tracking the approximate center of mass, the nose, the eye, or the foot. Some groups chose to track a spot on the kangaroo’s torso, reasoning that the approximate center of mass would tell them more about the movement of the kangaroo as a whole while avoiding the confounding effects of the internal motion of the kangaroo’s limbs. Several groups chose to track the kangaroo’s nose, noting that this gave them a spot that would be easy to identify in each frame and that the kangaroo’s head did not bob much as it was jumping. Ultimately, we left the final tracking choices up to each student group, although we steered some groups away from options that would detract from the main objectives of the day’s lab.
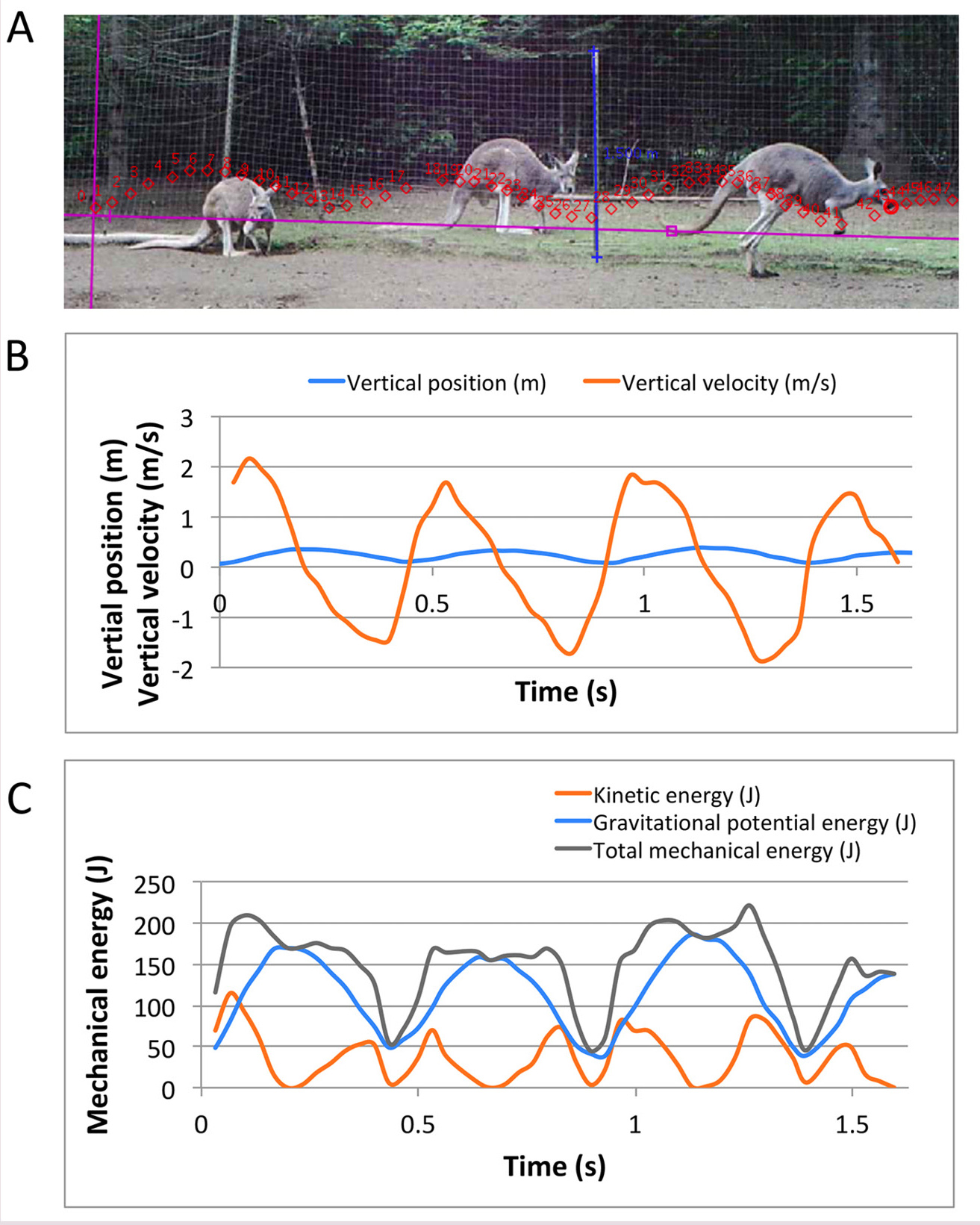
Case study Day 2: Video analysis of a red kangaroo hopping on flat ground.
Note. (A) Screenshot of a hopping kangaroo in the Tracker video analysis platform used in the class. (B) Sample student data tracking the vertical position and velocity of the hopping kangaroo. This group tracked the kangaroo’s nose as a proxy for its overall motion. (C) Sample student data showing calculations of gravitational potential energy, kinetic energy, and total mechanical energy corresponding to the motion data in part B. The video was recorded with permission at the Outback Kangaroo Farm: Wildlife Park in Arlington, Washington (Online Appendix 3).
Students noted some similarities between the energy graphs for the ball and the kangaroo. While airborne, the kangaroo and ball both exhibit a trade-off between gravitational potential energy and kinetic energy, with relatively constant mechanical energy. However, unlike the ball, the kangaroo rebounds to approximately the same height after each hop (Figures 1C and 2C). Two distinct explanations for this difference emerged in group discussions of the data: (a) In contrast with the ball, the kangaroo can replenish its supply of kinetic energy by using metabolic energy in the form of force produced by their muscles. (b) In contrast with the ball, the kangaroo may be more efficient in retaining its mechanical energy when it lands. For instance, the kangaroo may store more elastic potential energy or generate less relative heat when striking the ground. In our follow-up class discussion, we highlighted each of these hypothetical explanations and asked students to think about what evidence they would need to test each hypothesis.
Day 3: Analysis of metabolic energy expenditure
Extending our investigation of energy transformations in kangaroo locomotion, the third day of class was spent on a structured tutorial in which students worked in their small groups to interpret graphical data related to metabolic energy expenditure. We explained that researchers use oxygen consumption as an indirect measurement of the metabolic chemical reactions that power muscular contractions during locomotion. Experimental data showing how measured oxygen consumption depends on locomotion speed for different animals were recreated from published research for clarity (Figure 3; see Dawson & Taylor, 1973; Proske, 1980; Taylor et al., 1970).
To understand the data, students must first become familiar with how animals’ gaits change as they increase speed. Dogs, for instance, follow a common pattern of gait changes for four-legged (quadrupedal) animals changing from a walk to a trot to a galloping gait. As a dog increases its speed, metabolic energy expenditure increases proportionally (Figure 3A). Students noted that this trend is consistent with their personal experience with feeling more fatigued when jogging or running at faster paces.
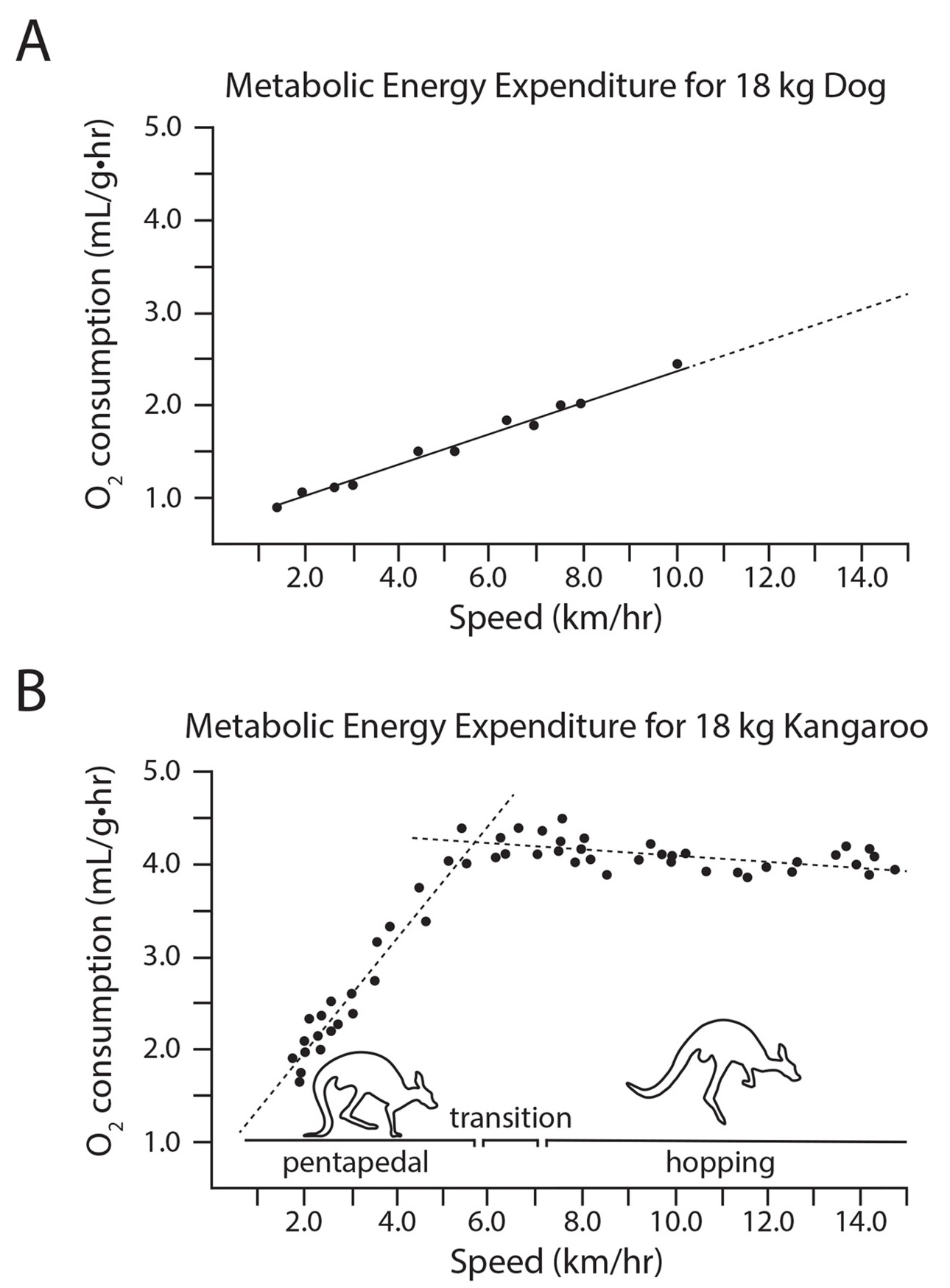
Case study Day 3: Analysis of metabolic energy expenditure.
Note. (A) Experimental measurements of a dog’s oxygen consumption as a function of locomotion speed. (B) Experimental measurements of a kangaroo’s oxygen consumption as a function of locomotion speed. These data are recreated from published research for clarity (Dawson & Taylor, 1973; Proske, 1980; Taylor et al., 1970).
In contrast, kangaroos use a pentapedal gait at slow speeds, using their tail as an additional powered limb (O’Connor et al., 2014), but switch to a bipedal hopping gait at moderate to high speeds. At slower speeds, when the kangaroo uses a pentapedal gait, metabolic energy expenditure increases with increasing speed similar to the dog (Figure 3), which is seemingly consistent with the hypothesis from the previous day that kangaroos supplement lost mechanical energy with metabolic energy. However, when the kangaroo begins to hop, metabolic energy expenditure does not continue to increase with increasing speeds (Figure 3). The decoupling of metabolic energy expenditure and speed during kangaroo hopping suggests that something different is going on when kangaroos hop. Many students returned to the second hypothesis from the previous day, speculating that kangaroos may store large amounts of elastic potential energy to support the hopping motion.
In a concluding mini-lecture, we highlighted research articles that tested the elastic properties of kangaroo tendons, providing supporting evidence for the role of elastic potential energy in efficient hopping (Biewener & Konieczynski, 1978; Proske, 1980). We also led a class discussion of some key observations from all 3 days of the kangaroo case study: (a) Energy can transform from one form to another within a system; (b) energy can transfer from a system to the surroundings; and (c) energy transformations play an important role in living systems, but a higher degree of internal complexity can make the flow of energy more challenging to describe.
Assessment of learning gains in energy concepts
Our informal observation of classroom interactions and students’ written responses suggested that students enjoyed learning principles of physics in the context of kangaroo locomotion. Students seemed keen to explore the ways in which energy flow of a simple object such as a bouncing ball translated to a complex living system like a kangaroo. Our case study is designed as a learning progression (Smith et al., 2006) to help students develop a more sophisticated grasp of energy flow in living systems. The guided tutorials provide opportunities for students to engage in quantitative reasoning and computational modeling practices that are increasingly relevant for careers in the life sciences (Hoskinson et al., 2014).
Two-question conceptual assessment surveys, selected from established multiple choice energy assessment tools (Ding et al., 2013; Singh & Rosengrant, 2003), were used to probe students’ understanding of energy flow within and out of a system. Questions 1 and 2 probe student understanding of energy transfer between systems and reasoning about energy transformations within a system, respectively. Of the 18 students in our class who completed the pre- and post-assessment surveys, 13 students answered Question 1 correctly in the post-quiz and 7 students answered Question 2 correctly in the post-quiz (Online Appendix 4). While this is not a statistically significant population, our initial probe of student learning provides some insight into how our students’ thinking on specific energy concepts developed. Figure 4A shows a typical student response to pre-lab quiz Question 1, and Figure 4B shows the post-lab quiz Question 1 response from the same student. In these responses, the student first identifies that energy exists, but the student has a misconception that energy is somehow cancelled upon collision; the student’s post-lab answer identifies that energy cannot be created nor destroyed and is therefore “transferred into thermal … energy.” Figure 4C and 4D show typical responses to pre-lab and post-lab quiz Question 2 from a different student. In these responses, the student first misidentifies that “energy expelled is at least kept constant or increase(s),” while the post-lab answer explains that “kinetic energy is traded for gravitational potential energy—keeping the total … constant.”
| Table 1. Parameters used for video analysis of mechanical energy. | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||

Lesson assessment quiz.
Note. (A) Sample student response to pre-lab quiz Question 1. (B) Response to post-lab quiz Question 1 from the same student as in A. (C) Sample student response to pre-lab quiz Question 2. (D) Response to post-lab quiz Question 2 from the same student as in C. Our two-question conceptual assessment survey used selected questions from established multiple choice energy assessment tools (Ding et al., 2013; Singh & Rosengrant, 2003).
Supporting diverse learners
In designing and implementing the kangaroo case study, one of our goals was to support the learning process of all students, including English language learners, students with disabilities, and learners from other traditionally marginalized groups. This case study aligns with several recommendations of the Universal Design for Learning (UDL) framework, which outlines research-based principles and associated checkpoints for accessible curriculum (CAST, 2018; Scanlon et al., 2018). Here are some examples of such checkpoints:
- UDL framework checkpoint: Activate and supply background knowledge. A challenge in physics education is to bring concepts to life using real-life examples that are relatable to students from many cultural backgrounds. Most students in our class had little prior experience observing or studying kangaroo locomotion, which essentially put everyone on equal footing. To help students gain new physical insight from a novel situation, it helps to build on established knowledge in a more familiar context. For this reason, we began our case study by examining the motion of a bouncing ball, a familiar type of motion that has the added benefit of being simple to demonstrate in class. During each day of the case study, key terms and concepts were defined explicitly so that field-specific vocabulary did not create a barrier for any student (see Figure 5).
Key NGSS vocabulary terms for energy.
Energy: the capacity to do work
Kinetic Energy: energy of movement
Potential Energy: stored energy
- Gravitational Potential Energy: energy a physical object with mass has due to its location in a gravitational field
- Elastic Potential Energy: energy an object has as a result of being deformed (compressed or stretched) by the application of external force
- Chemical Energy: energy stored in chemical bonds of compounds.
- Metabolic Energy: regulated conversion of chemical energy stored in nutrients to other forms of kinetic and potential energy. Aerobic metabolism requires the consumption of oxygen gas.
Mechanical Energy: sum of potential and kinetic energy of an object (does not include chemical energy)
2.UDL framework checkpoint: Support planning and strategy development. The kangaroo case study is designed to provide a scaffold for students to develop their collaborative problem-solving skills. Our guided tutorials provide structure while allowing some flexibility for students to make choices in the context of their group discussions (such as selecting which point on the kangaroo to track). Students initially answer questions based on their direct observations (e.g., “In what portion of the ball’s motion is the velocity negative?”). As students progress through the case study, they are challenged to make inferences from the data, answering questions such as “Do you think the kangaroo exchanges energy with its environment at any point throughout its motion? If so, when does this take place?” By circulating around the room and talking with student teams, instructors can differentiate their questions and feedback to support all learners.
3.UDL framework checkpoint: Foster collaboration and community. The kangaroo case study is designed for students to work in small groups of three or four over the course of several days. There are a variety of ways for each person to contribute to the group, including sketching predictions, obtaining positional data from videos, making graphs, and discussing and interpreting results. While instructors may choose to assign roles to each group member, we opted to build in some time for the newly formed teams to discuss and plan their strategies for collaborating inclusively.
Conclusion
Science, technology, engineering, and mathematics (STEM) careers in the 21st century are increasingly interdisciplinary, requiring scientists and engineers to integrate the tools and concepts of multiple traditional disciplines to analyze complex systems. The case study presented in this article is designed to help students develop a capacity for interdisciplinary scientific inquiry by having them use computational modeling and physical reasoning to analyze a living system. The guided tutorials for small-group discussions are intended to facilitate learning progressions from a simpler nonbiological context (a bouncing ball) to a more complex biological system (Online Appendices 5, 6, 7, 8, 9, and 10).
We expect that the lessons could be flexibly adapted to fit the needs of varied classroom settings. For example, a class on a tight schedule could choose to analyze motion data from the videos provided (Online Appendices 2 and 3), whereas students can record their own movies and even design their own follow-up investigations if class time allows. Although we designed the kangaroo case study with a face-to-face class modality in mind, the activities could be adapted to an online learning environment using freely available video-tracking software. Our own attempts to adapt video analysis activities to an online environment during the COVID-19 pandemic were hindered by limitations in student access to computers that could run the tracking software. One work-around to this challenge is for the instructor to demonstrate the data collection process and provide students with the numerical data so they can perform the analysis.
A highlight for us was to see the creative ways in which students applied the tools and approaches of the kangaroo case study to develop their own extended projects later in the quarter. Students in our class chose to analyze other forms of animal locomotion, such as rabbits hopping, cats leaping, mantis shrimp forelimb striking, and birds flying.
Erin M. Craig (erin.craig@cwu.edu) is an associate professor in the Department of Physics, Derek Ricketson (derek.ricketson@cwu.edu) is a senior lecturer in the Department of Chemistry, and Timothy Sorey (tim.sorey@cwu.edu) is a professor in the Department of Chemistry, all at Central Washington University (CWU) in Ellensburg, Washington. Sydney Galbreath (sydney.galbreath@cwu.edu) graduated from CWU in 2021 with a degree in biochemistry and is now enrolled in the Washington State University College of Pharmacy in Spokane, Washington.
Biology Instructional Materials Interdisciplinary Physical Science


