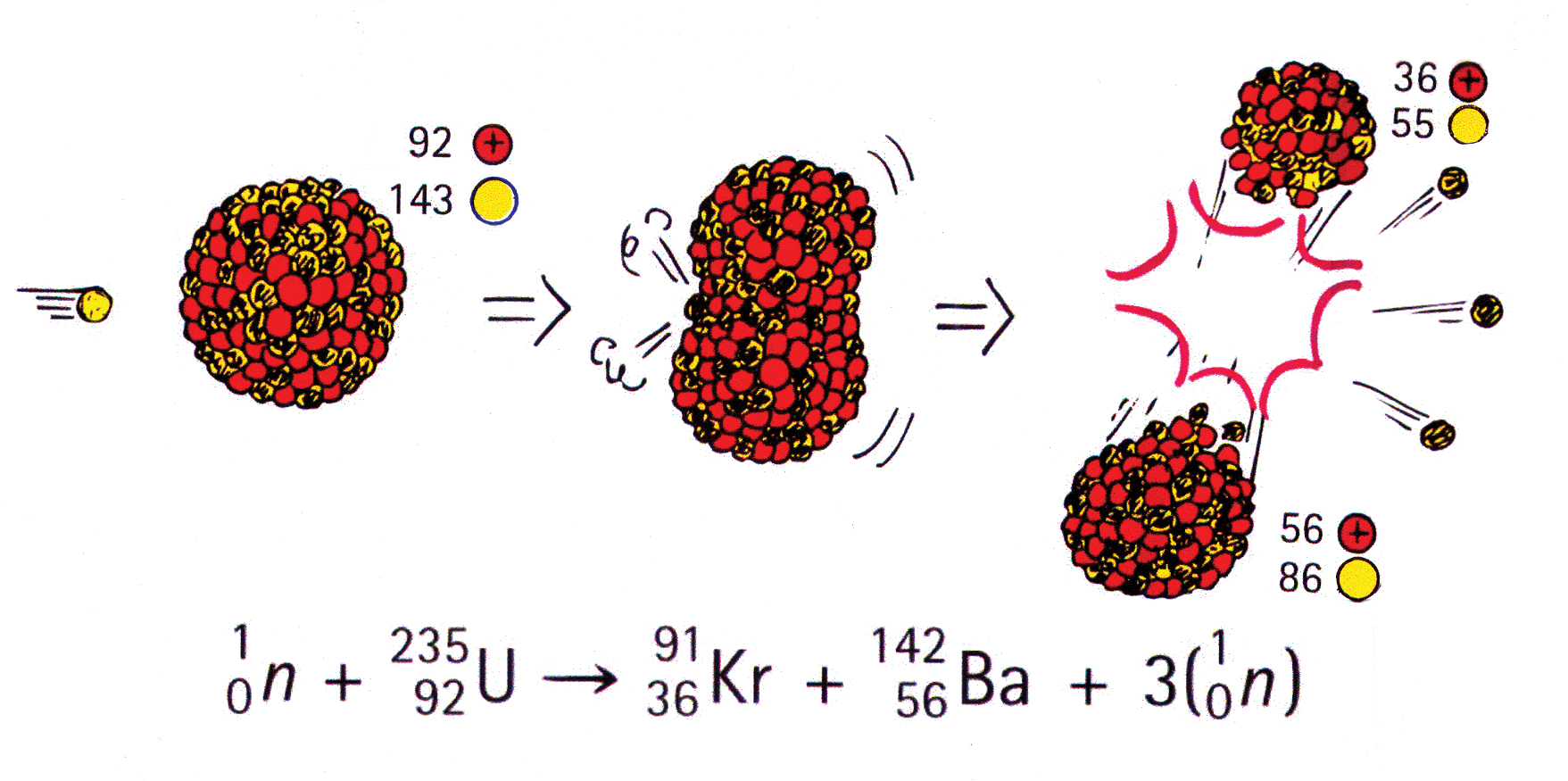
But most astounding is the energy released, some 200 million electron volts (eV) of energy per nucleus (an electron volt is a unit of energy equal to 1.6 × 10^-19 joule). In comparison, about 2 eV of energy per molecule is involved in chemical reactions. Where does this nuclear energy come from? The answer has to do with a discovery made by Albert Einstein in 1905.

Mass-energy equivalence
Einstein discovered an amazing connection between mass and energy: Mass is actually “congealed” energy. Mass and energy are two sides of the same coin, stated in Einstein’s celebrated equation, E = mc². In this equation, E stands for the energy that any mass has at rest, m stands for mass, and c is the speed of light. The quantity c² is the proportionality constant between E and m, a huge number that reveals how a tiny amount of mass converts to enormous energy. E = mc² is the key to understanding why and how energy is released in nuclear reactions.

Nuclear mass versus the mass of free nucleons
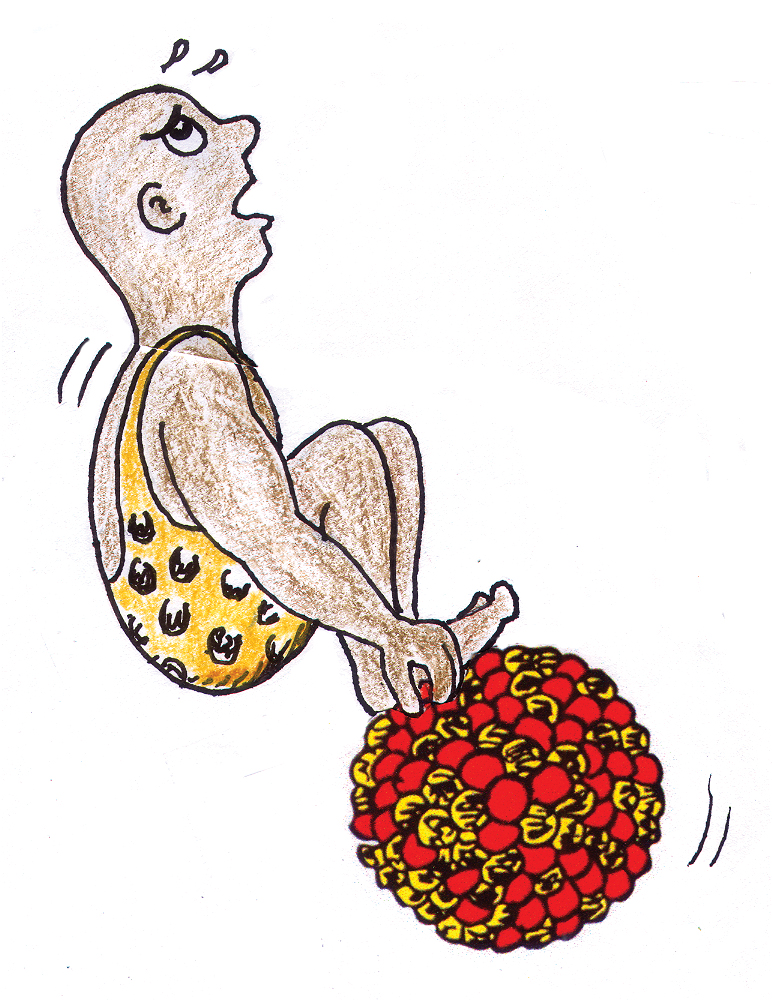
Two concepts are central to both nuclear fission and fusion: First, the mass of a nucleus is less than the sum of the masses the nucleons would have if they were free. This is called the mass defect.

Consider the work required to separate nucleons from a nucleus (Figure 2). Recall that work is expended energy equal to force × distance. On the atomic scale, appreciable force is required to pull a nucleon out of an atomic nucleus through a sufficient distance to overcome the attractive strong force that holds the nucleus together. What becomes of this work? In accord with E = mc², the energy that is expended adds to the mass of the liberated nucleon. So we see that a free nucleon has more mass than a nucleon locked inside the nucleus. Conversely, when nucleons bind together to form a nucleus, they release energy, called binding energy, losing the equivalent mass.

Mass per nucleon versus atomic number
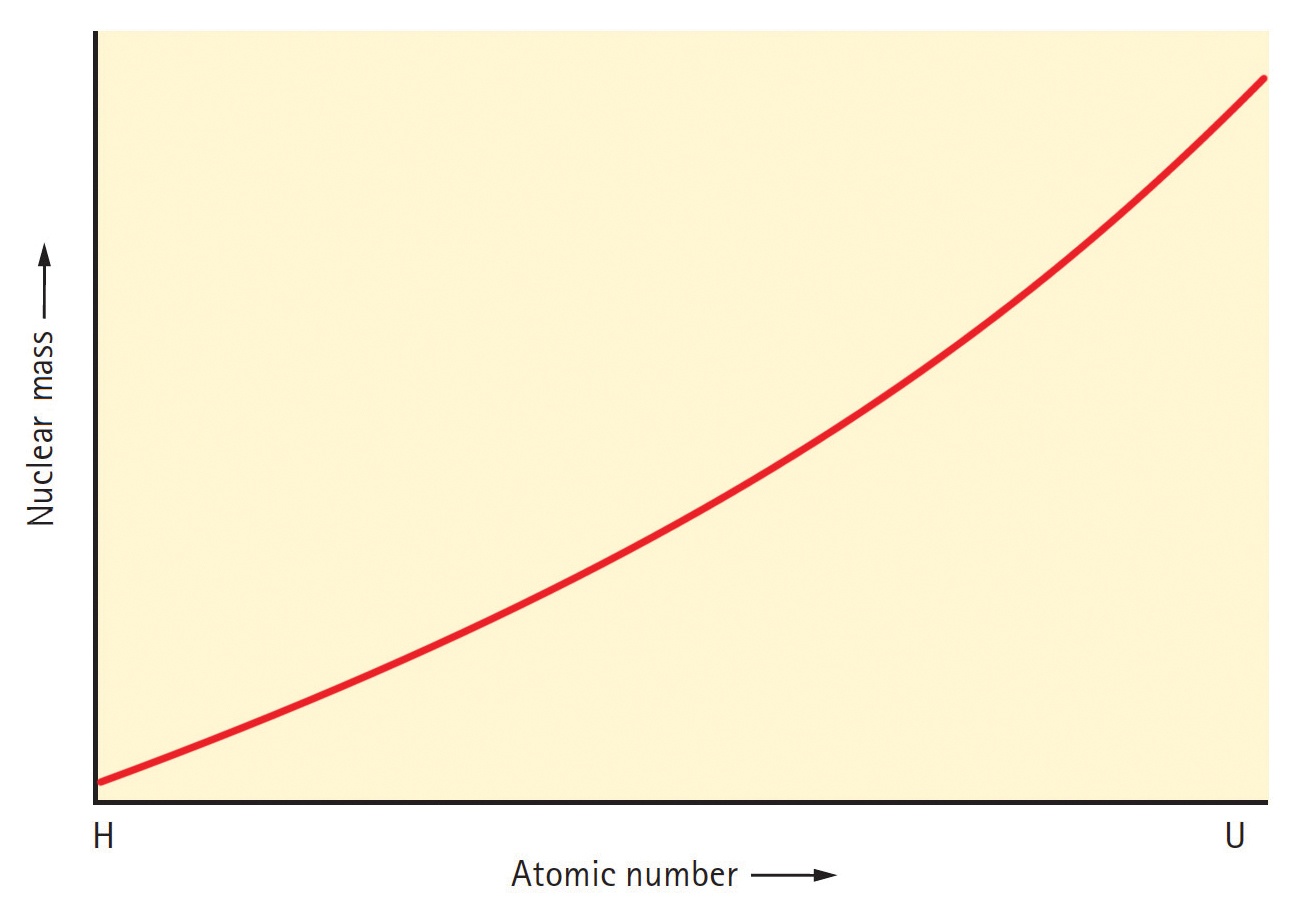
Secondly, the mass per nucleon varies from hydrogen to uranium in an extremely significant pattern. Figure 3 is a graph of nuclear mass versus atomic number (number of protons) for atoms ranging from hydrogen to uranium. As you might expect, the graph slopes upward with increasing atomic number, which simply indicates that the higher the atomic number, the more massive the nucleus.

A more important and very different graph is a plot of mass per nucleon versus atomic number (Figure 4). Not only does a nucleus have less mass than the sum of the masses of its free nucleons, we see the mass per nucleon varies from element to element.

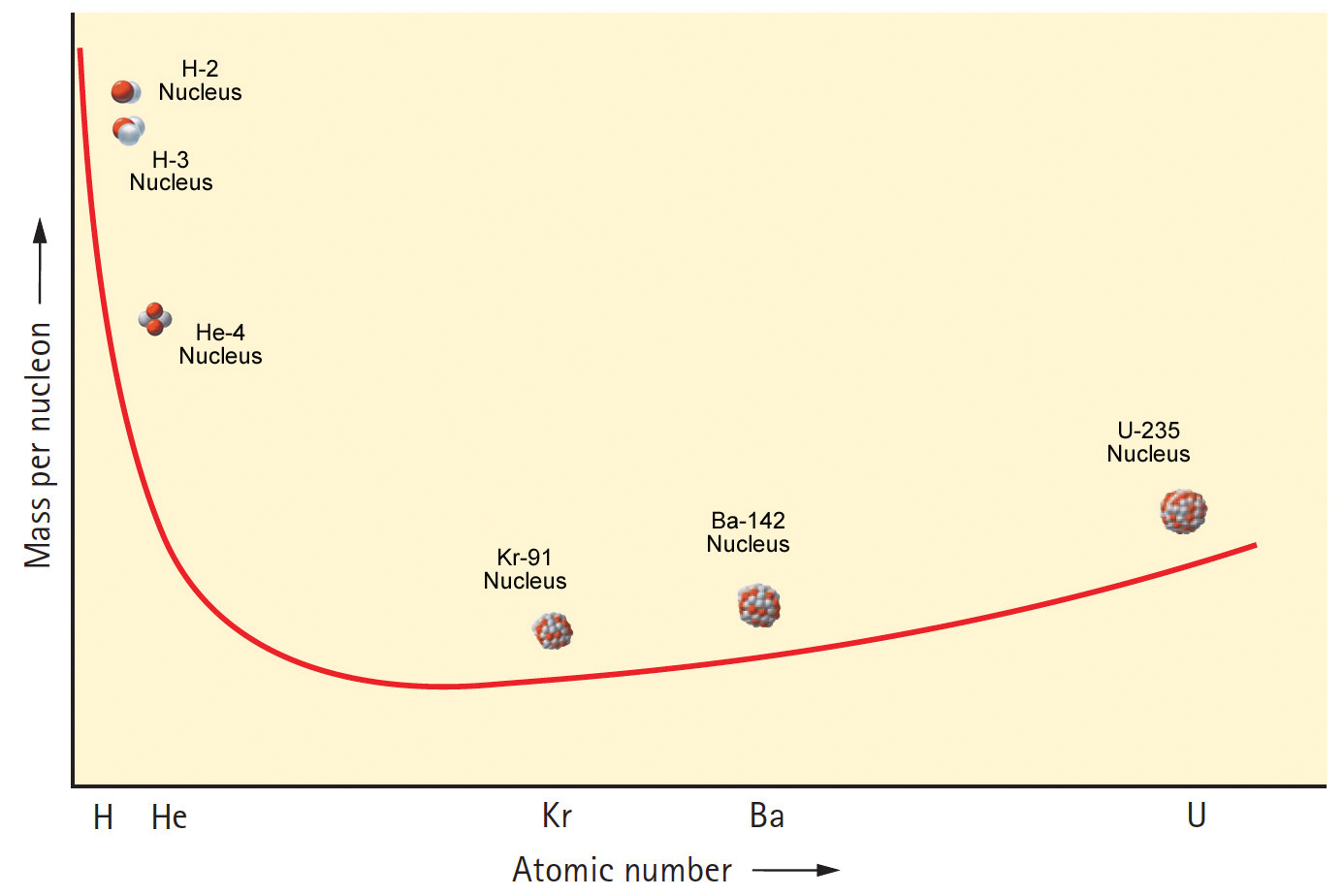
I regard Figure 4 as the most important graph in a study of nuclear physics. It is essential to understanding the energy associated with all nuclear processes—particularly nuclear fission and fusion. We can think of this curve as an “energy valley” that starts at the highest point (hydrogen), slopes steeply down to level off at the lowest point (iron), and then slopes gradually upward to uranium.

Fission and fusion
The graph in Figure 4 tells us that the fission of uranium produces elements lower on the curve. That lowered mass per nucleon converts to energy via E = mc².

In today’s world, all nuclear power plants employ fission. A possible long-range source of energy now being vigorously studied makes use of the left side of the energy valley—nuclear fusion—the opposite of nuclear fission.

Whereas fission is the breaking apart of atomic nuclei, nuclear fusion is the combining (fusing) of atomic nuclei. The left side of Figure 4 shows that isotopes of hydrogen are located at the highest and steepest part the energy-valley curve. They fuse to become helium that is lower on the curve. Since helium has less mass per nucleon than hydrogen, then, as with fission, lowered mass means energy release.

Typical fusion reactions employ hydrogen isotopes: the heavy isotope hydrogen-2, deuterium, or the heavier isotope hydrogen-3, tritium (Figure 5).

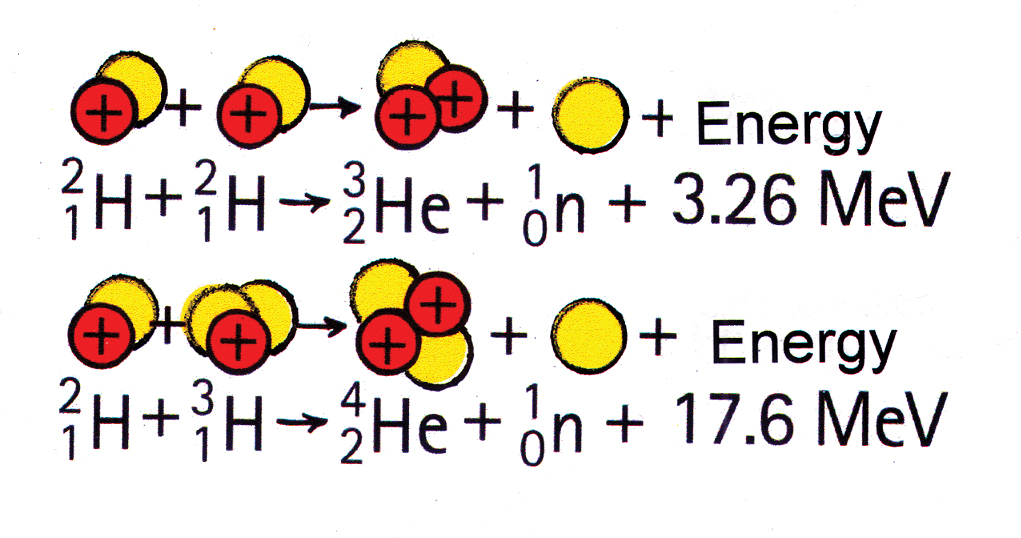
The name of the game in all nuclear reactions is this: Decreased mass is accompanied by release of energy. Energy release occurs when the products of either fission or fusion are lower on the curve, downhill in the energy valley. The mass converted to energy in fission is about 0.1%; in fusion it can be as much as 0.7%. These numbers apply whether the process takes place in reactors, bombs, or stars. The high temperatures associated with these nuclear reactions are due chiefly to the kinetic energy of the reaction products, particularly the neutrons.

The product of fusion is never a sole helium nucleus. Typically, two particles are produced, as shown in Figure 5. There is no instance in nature in which mass transforms into energy (or vice versa) without some material particle carrying that energy. In addition to the helium nucleus formed in fusion, there must be a neutron to carry energy away.

The rate at which fusion occurs can vary. Interestingly, the fusion occurring continuously in the Sun is relatively slow. If it weren’t, our Sun would have burned out long ago. Although humans don’t yet use fusion to produce energy on Earth, keep tuned to the news as we work to tame this process that produces our sunshine and lights our nighttime stars.

Paul G. Hewitt (pghewitt@aol.com) is the author of the popular textbook Conceptual Physics, 12th edition, and coauthor with his daughter Leslie A. Hewitt and nephew John Suchocki of Conceptual Physical Science, 6th edition.

On the web
See complementary tutorial screencasts 132–137 on fission and fusion and 142 on E = mc² at www.HewittDrewIt.com.

Editor’s Note

This article was originally published in the December 2016 issue of The Science Teacher journal from the National Science Teachers Association (NSTA).

Get Involved With NSTA!

Join NSTA today and receive The Science Teacher,
the peer-reviewed journal just for high school teachers; to write for the journal, see our Author Guidelines, Call for Papers, and annotated sample manuscript; connect on the high school level science teaching list (members can sign up on the list server); or consider joining your peers at future NSTA conferences.