A: You might have heard that this has something to do with the Coriolis effect. However, the Coriolis effect (an apparent force resulting from the Earth’s spin) has virtually nothing to do with water swirling down a drain. This force has noticeable effects only on long-lasting motions and large bodies like oceans and large atmospheric phenomena such as hurricanes. The Coriolis force is much too weak to have any effect on short-lived phenomenon in small basins of water under normal conditions.

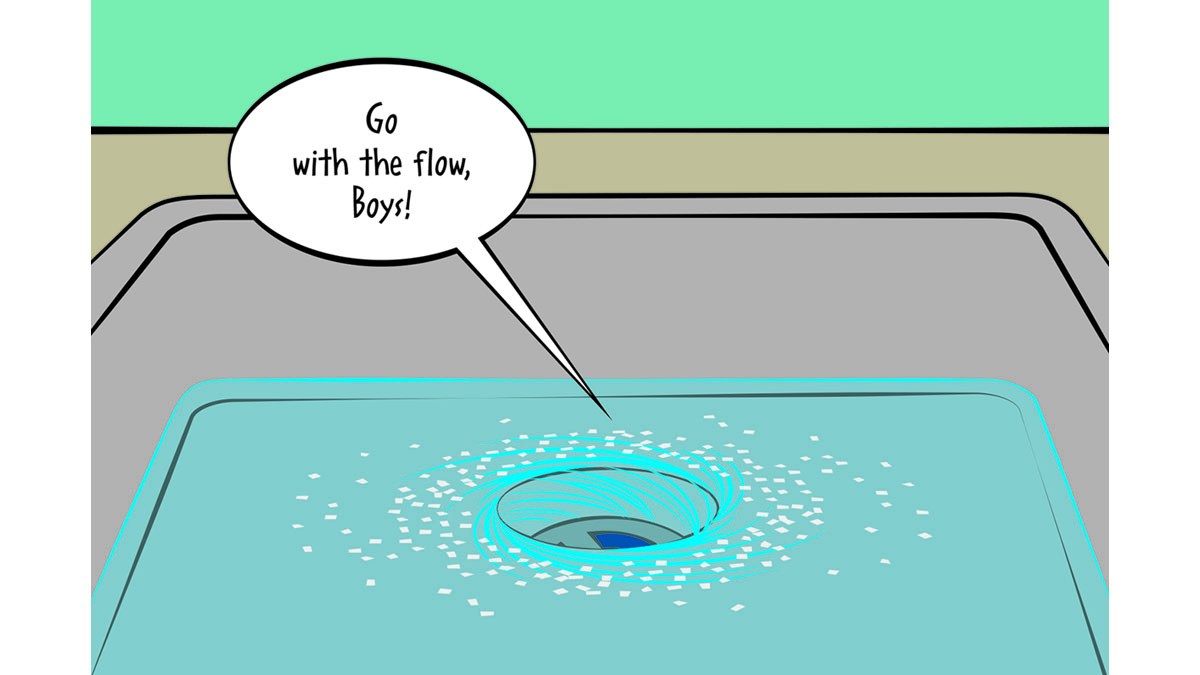
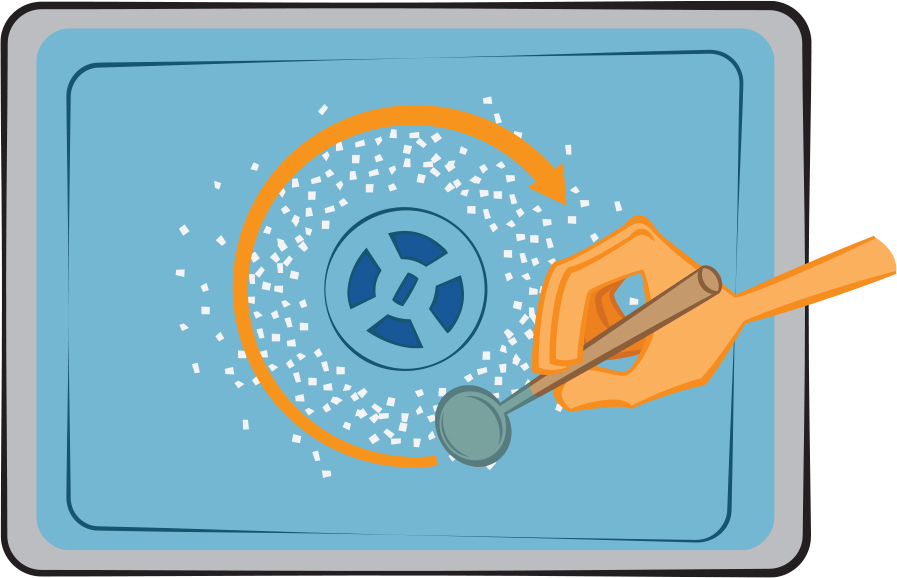
Before opening the drain, the water already has some motion, although it might be too slow for you to notice. As the water moves toward the drain, its rotational motion gets amplified, i.e., it starts swirling faster (see Figure 1). Students can easily confirm that the water ends up swirling down the drain in the same direction that it was originally moving. They start this investigation by filling up a sink with water. The rounder the sink, the better, although this isn’t essential. Keeping the stopper in the drain, stir the water around in one direction, say clockwise. (By the way, with the prevalence of digital watches and clocks, do your students these days know what clockwise means? I hope you have an analog clock in your classroom.) It might also help to have something floating in the water to make the motion more visible. For instance, sprinkle some pepper on the water right after stirring to see its motion more easily.

The students can stir the water with a large spoon, a stick, or, after rolling up sleeves, just with a hand (see Figure 2). Now wait a few minutes until the water is hardly moving and then open the drain. Students will then notice how the water ends up swirling down the drain in the same direction that they stirred it earlier. Repeat the experiment stirring counterclockwise. Students should conclude that the water swirls down the drain in the same direction that it was initially moving.

Do you have extra time to fill? (Ha ha.) If so, repeat the investigation waiting longer after stirring for the water to settle. Students may notice that even after they don’t see any more movement of the water, it still swirls down the drain in the same direction that it was stirred earlier. Thus even the slightest, imperceptible movement will get amplified into fast swirling.

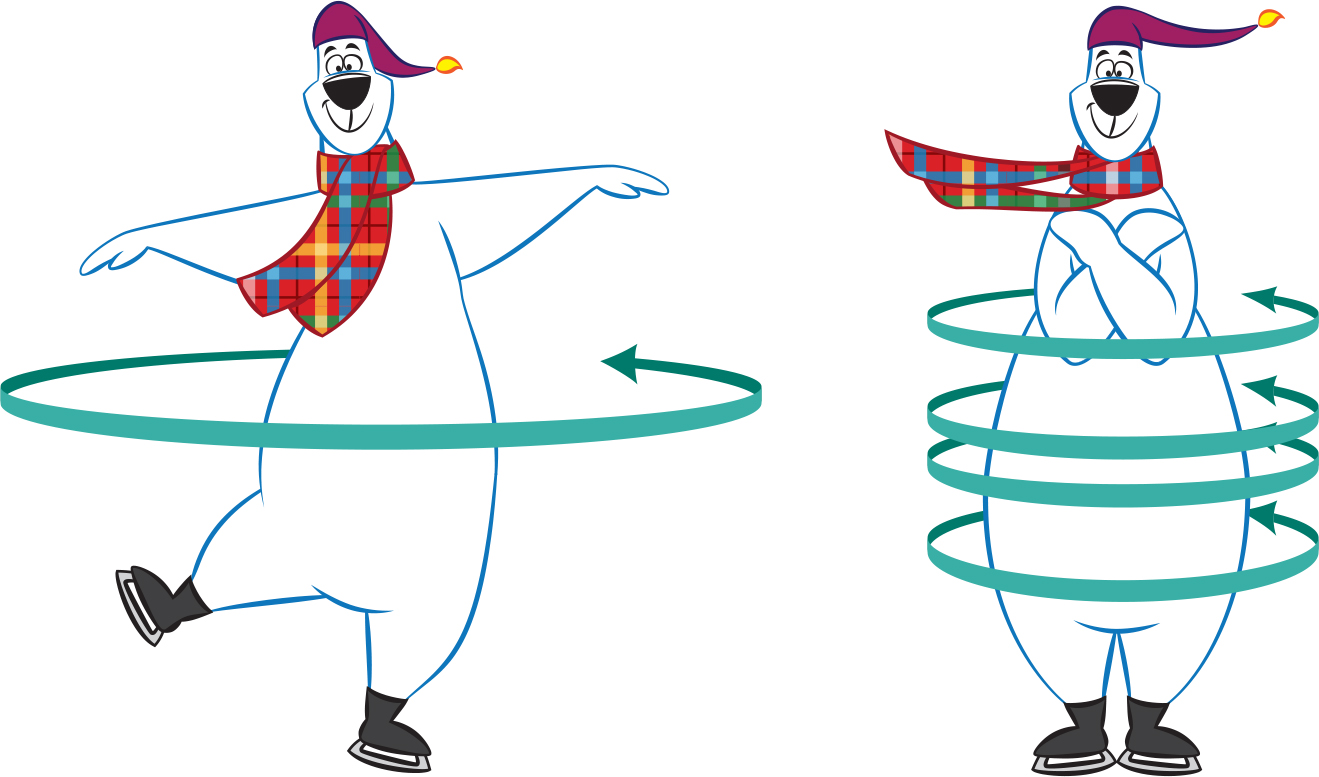
The reason this happens is the same as why a spinning ice skater will spin faster as she pulls in her arms and legs (see Figure 3). It has to do with a quantity known as angular momentum. The angular momentum is the product of three quantities: the mass of the object, the size of the object, and the spinning speed. Let’s write this as an equation:

For an object moving around in a circle, like a ball on a string being twirled around, the size in this case would refer to the distance of the ball from the center of the circle, i.e., the length of the string. Keep that in mind when we get back to the swirling water. And if students haven’t yet learned about mass, feel free to say “amount of matter” or “amount of material” or “amount of stuff” instead.

The key is this: If there’s no outside force pushing or pulling on the spinning object, the angular momentum stays the same. One last bit of terminology: When something stays the same, scientists say it is conserved. So the idea that the angular momentum stays the same is known as the conservation of angular momentum. That’s quite a mouthful, but after discussing it for while, you get used to it. And that’s the term that physicists use for this phenomenon, which is the basic principle that explains why the spinning ice skater speeds up, why the water swirls faster as it approaches the drain, and a variety of other phenomena. Let’s see how this works.

If the angular momentum stays the same, that means the product mass × size × speed stays the same. Now let’s consider each of those quantities individually. Ask students: When the spinning ice skater starts to pull in her arms and leg, which of those change and which stay the same? Does her mass change? (No.) Does her size change? (Yes! Since she’s pulling in her arms and leg, she’s making herself smaller, i.e., less spread out.) So let’s think about this…. If mass × size × speed stays the same, the mass stays the same, and the size decreases, how must the speed change? Well, the only way that mass × size × speed can stay the same if the size decreases is if the speed increases. And that’s exactly what happens to the spinning skater.

Let’s try this with some numbers. Suppose (excluding units for now), that the mass, size, and speed have these values:

Then we know that mass × size × speed = 48. Now let’s say that the spinning skater pulls in her arms and legs so that her size decreases from 6 to 3. What happens to her speed? The product of all three quantities must remain at 48, so

What number could the speed be that would make the product of all three numbers equal to 48? No algebra needed; with just using a little trial and error, we can discover that the speed must be 4, since 4 × 3 × 4 = 48. So the speed increased from 2 to 4.

Notice that when the size was divided by 2 (from 6 to 3), the speed was multiplied by 2. That’s how it always works. If the size had been divided by 3, the speed would have been multiplied by 3. In general, if the size decreases by some factor, the speed increases by that same factor. The opposite is also true: If the size increases by some factor, the speed decreases by that same factor.

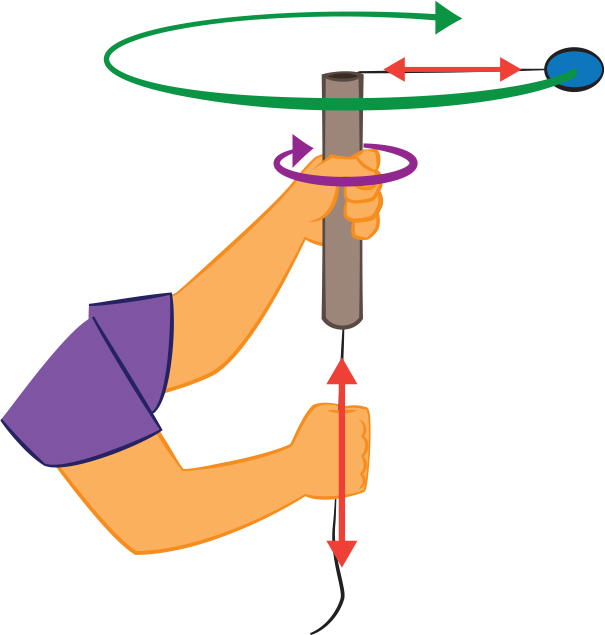
You can demonstrate the conservation of angular momentum with a simple gadget made from a ball—or any object—on a string and a small tube. (This can be a short length of PVC pipe or any rigid tube you can find.) Let the string attached to the ball pass through the tube (see Figure 4). Holding the tube and twirling it around, you can spin the ball around in a circle. (Make sure the inside edges of the tube are not sharp; otherwise they will cut the string as it twirls around.) With your other hand, hold the string at the bottom to adjust the amount of string coming out the top. Start the ball twirling far away, and then pull down on the string to draw the ball closer. Notice how it speeds up.

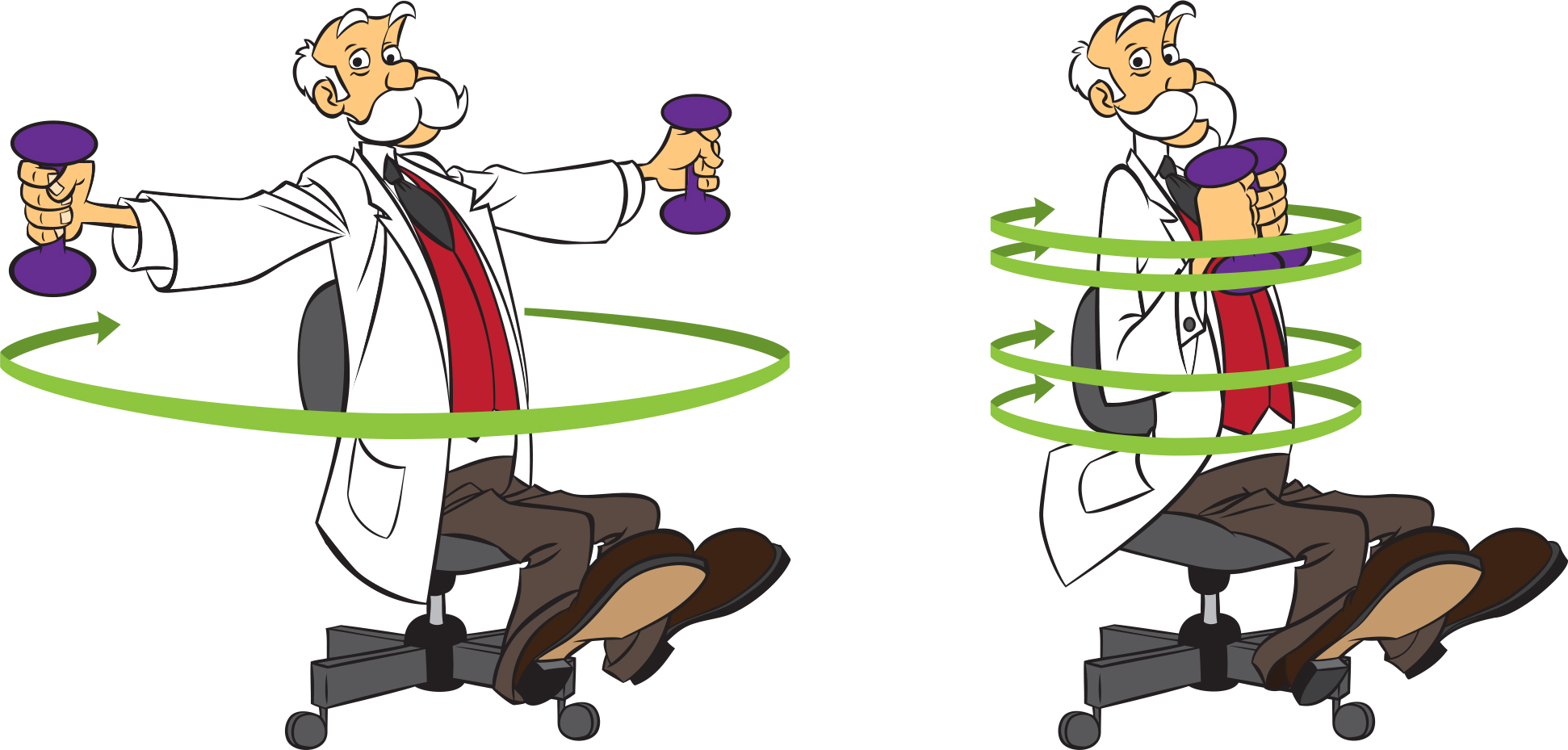
You can also demonstrate the conservation of angular momentum by spinning around in a swivel chair. While sitting in the chair, hold weights out at arm’s length. See Figure 5. (Use weights that are as heavy as you can hold. The more massive they are, the better this works.) Then someone starts the chair slowly spinning. While spinning, pull in the weights, and the speed increases. Extend arms again, and the spinning slows down.

This effect accounts for the spinning ice skater as well as the water swirling down the drain. As the water moves around, gravity pulls it closer to the drain. Any particular drop of water gets closer to the drain just as the ball got closer to the tube. As that distance decreases, the “size” in the equation decreases. So, for the product mass × size × speed to remain the same, the speed must increase.

What are some of the places where we see this phenomenon? Here are a few other real-life examples, along with a description of how the “size” decreases, causing the rotation to speed up:

• Hurricanes—The air gets pushed toward the low-pressure region at the center, causing its circulation to speed up.
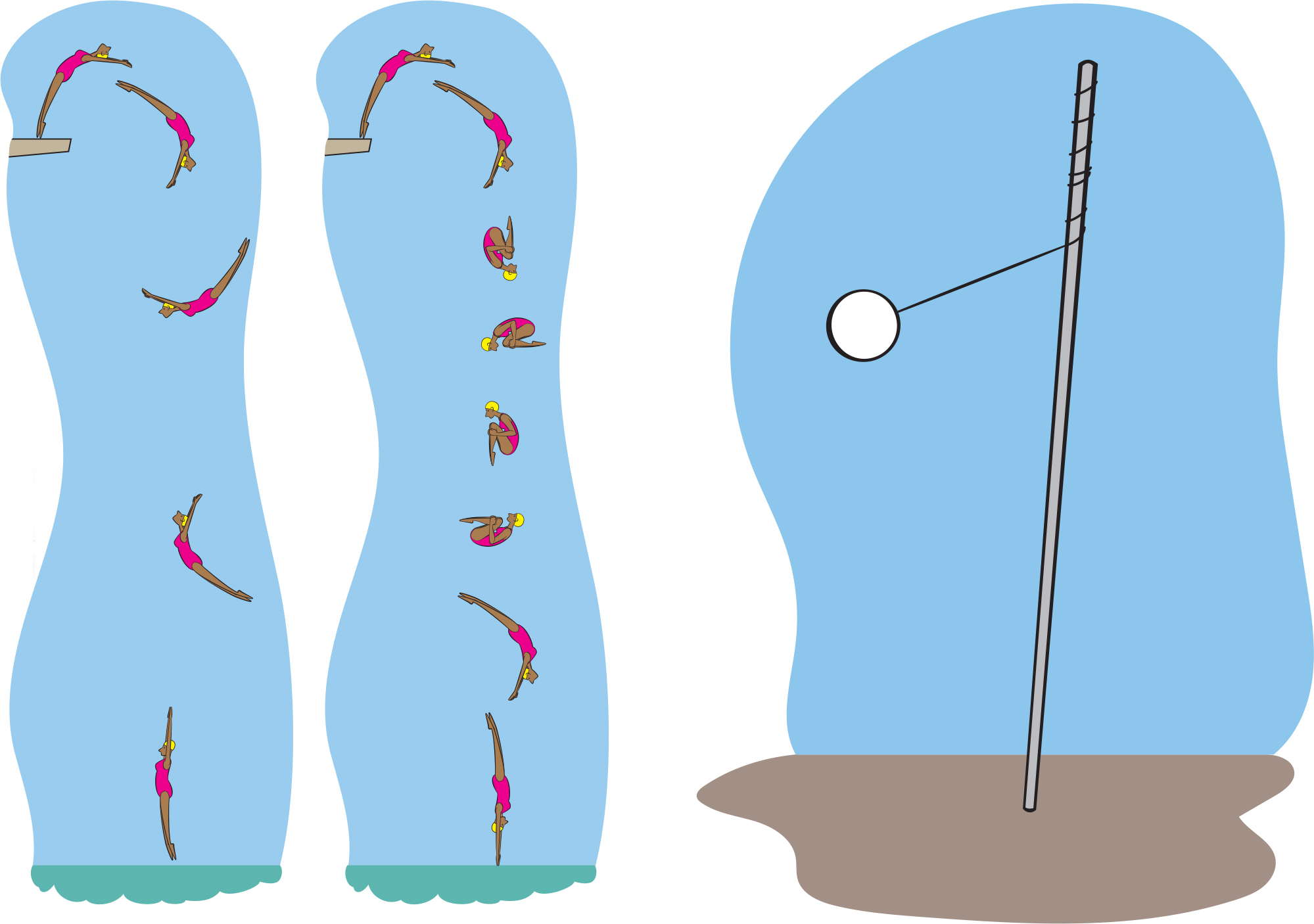
• Tetherball—No longer found on many playgrounds, but a perfect example: As the ball goes around, the rope winds around the pole, pulling the ball closer, which causes the ball to speed up.
• Gymnast or diver doing a flip—After the diver jumps off the diving board, he tucks his body into a ball to increase his speed of rotation. Then he extends his body to slow down the rotation for the final plunge.
• Comet—As a comet orbits the Sun, its orbit is elongated, so it sometimes gets closer to the sun and sometimes gets farther from the Sun. As it gets closer, it speeds up; farther from the Sun, it slows down.

In all of these cases (a few illustrated in Figure 6, p. 71), as something gets smaller or closer to the center of the rotation, it speeds up; and as it gets larger or farther from the center, it slows down. All of this happens because the angular momentum, mass × size × speed, stays the same.

The most common misconception about all of this, which I mentioned right at the beginning, is that the water swirls down a drain due to the Coriolis effect (it doesn’t) and that the water swirls down a drain in the opposite direction in the Southern Hemisphere compared to the Northern Hemisphere (it doesn’t). As we saw from our investigation, the water swirls in whichever direction it was moving to start with. Or, if there is little or no water movement, the direction of swirling will be determined by the shape of the basin. In the case of a toilet, the water usually gets squirted into the bowl through holes that direct the water in a particular direction. That direction determines which way the water swirls down the drain.

If you visit a place located at the equator, there are often charlatans who—for a small fee—will purport to demonstrate that water swirls down a drain in a different direction, depending on which side of the equator you’re on. (I saw this done in Ecuador; see Figure 7.) There are plenty of YouTube videos of this. They’re all fake, as you can get the water to swirl in either direction depending on which way you start the water moving to begin with—which is what they do to fool people. For everyday situations involving sinks and toilets, which hemisphere you’re in has absolutely no bearing on which way the draining water spins. I hope that didn’t make your head spin.

Never stop learning!