A:Yes, I know, the question should really have been, “Why is the Earth approximately spherical?” The word round is a bit ambiguous, as it could refer to a two-dimensional circle or a three-dimensional sphere. For the youngest students, we could ask, “Why is the Earth shaped like a ball?”

You might have noticed that there are some people who question whether the Earth is really round, or who actually believe (or claim to believe) that it’s flat. That shows a major failure in our educational system. But you and I will help change that!

These “flat-Earthers” try to argue that a flat Earth can explain all of our observations and, at the same time, they claim that photos and video of the Earth taken from space showing a rotating, spherical Earth are all fakes. This is nonsense, of course, and there’s one particular scientific fact that they aren’t aware of: Regardless of the observations and how we may or may not be misled by them, the Earth MUST be round! The laws of physics require it. Let’s explore why that is.

Try this: Without any introductory comments, give each student—or group of students—a brick-shaped piece of clay or Play-Doh. (Recipes for making a homemade version of Play-Doh can be found on the internet.) The task for students is this: Form the Play-Doh into a shape that has the smallest outer surface (i.e., surface area). Here’s another way of framing the task: Tell students to imagine that, after they’re done shaping the Play-Doh, they’re going to paint it. And they need to use as little paint as possible. What shape will require the least amount of paint to cover it? If they need a hint, you can point out that if, for example, they were to flatten their Play-Doh into an extremely thin, broad sheet, this shape would have a lot of surface to paint (see Figure 1). So that wouldn’t be the best shape to make if you want to use the least amount of paint.

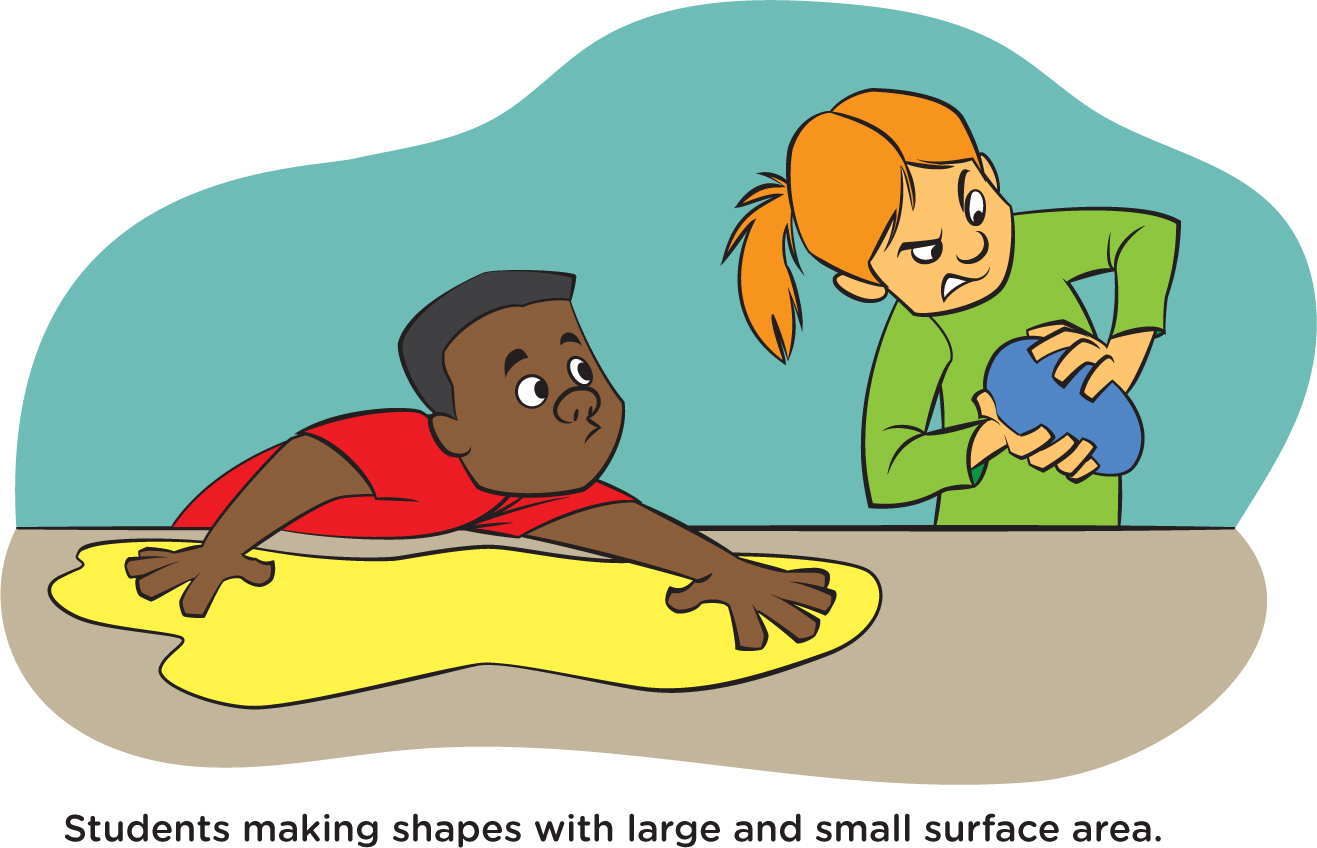
As students try to reduce the surface area, what you should observe is that—in an attempt to make the surface as small as possible—they squeeze their Play-Doh into a shape like a ball (or sphere), which is the correct answer. That’s the shape that has the least amount of surface area for any amount of Play-Doh. Of all possible shapes—hot dogs, rings, cubes, irregular lumps—a sphere has the smallest amount of outside area. You can also think of it as the most compact shape, with all parts of the Play-Doh as close to each other as they can get.

Reflect on how students made the Play-Doh into a ball. They squeezed it from all directions (see Figure 2). So whenever a shape is squeezed together from all directions, it forms a sphere. To see an example of this, students can blow some soap bubbles. As soon as the bubble leaves the wand (or whatever gizmo they’re using to make the bubbles), the bubble immediately becomes round (see Figure 3). No cubical bubbles, no pyramids, no pancake-shaped bubbles—just spheres!

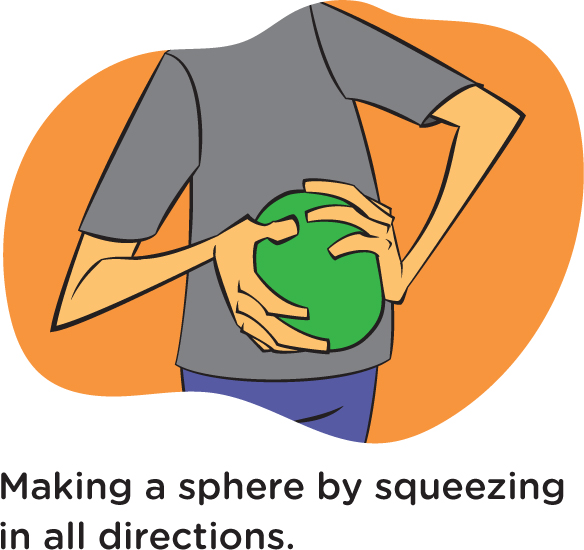
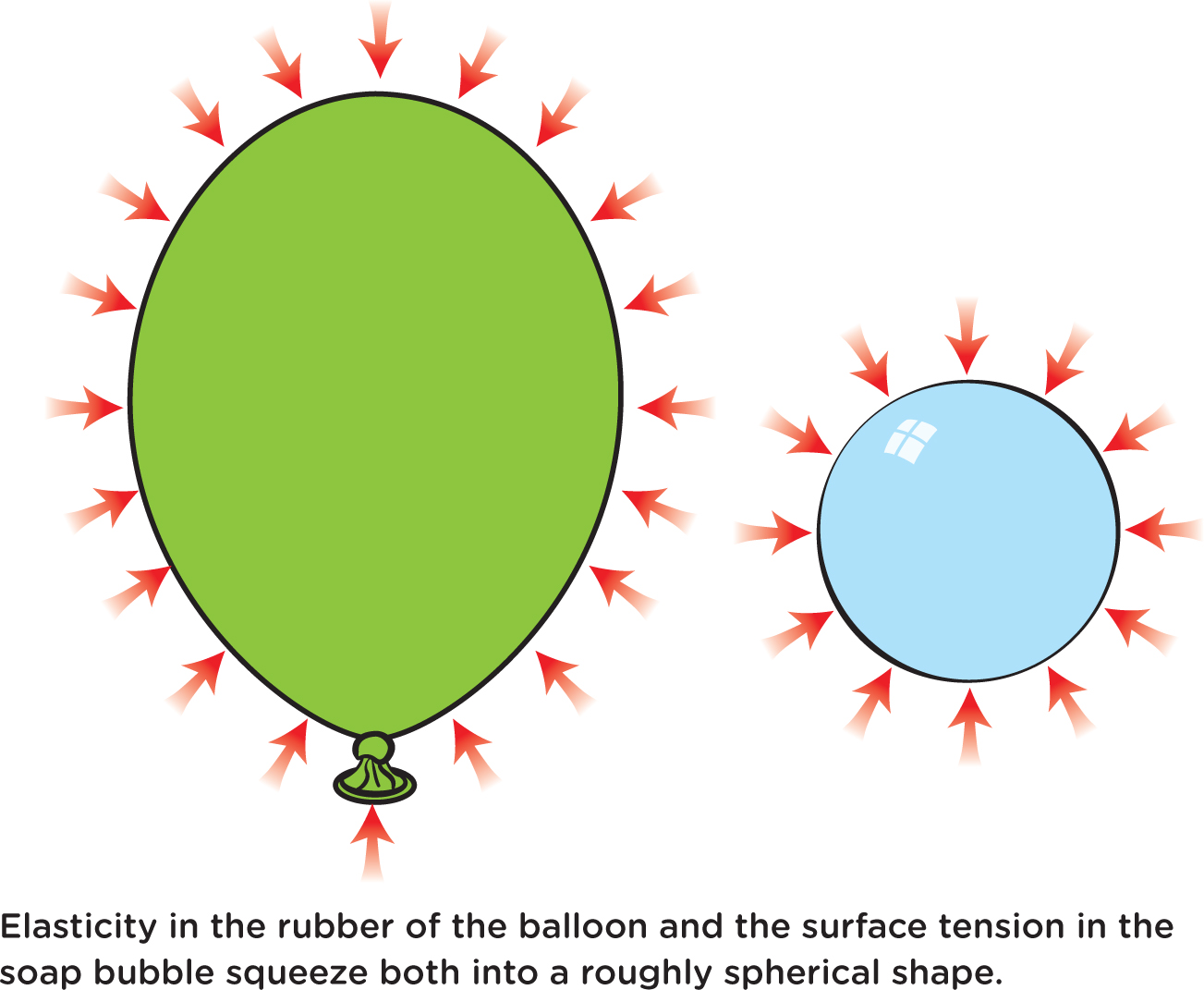
Remembering what happened with the Play-Doh, students can try to think of something similar that might be happening with the soap bubbles. Just as pushing on the Play-Doh from all directions makes it into a sphere, there must be something pushing or pulling the soap bubble from all directions to form a sphere. And indeed there is. The surface of a soap bubble is kind of elastic—like the rubber of a balloon, which is also usually somewhat round. Technical nitty-gritty: It’s elastic because the molecules in the soap solution are attracting—pulling—on each other due to the attraction of opposite electrical charges. The collective attraction all over the surface is called surface tension.

The rubber in a balloon does something similar, except that the rubber is thicker in some places than others, and there’s also a knot; the balloon is not quite symmetrical and ends up deviating from the spherical shape that we see with a soap bubble (see Figure 4). But the balloon usually has a somewhat roundish shape.

So, summing up what we’ve said so far…whenever an object gets squeezed equally from all directions, it creates a spherical shape—or close to it. Ask students, “Could this apply to the Earth as well? What could be squeezing or pulling on the Earth from all directions?” Let them discuss this with each other in pairs or groups. Depending on the grade level of your class, it might not be long before someone answers that the cause of the pulling on the Earth is gravity!

Gravity pulls on the Earth from all directions (see Figure 5) and keeps any part of the Earth from sticking out very far. Just as squeezing the Play-Doh from all directions made the Play-Doh round, gravity does the same thing to the Earth. But, a student may ask, what about mountains that stick up, like Mt. Everest? Mt. Everest is about as big as a mountain could possibly be on the Earth. If you tried to make a mountain much higher than Everest, the rock at the bottom would get crushed or melted, and the mountain would start to collapse.

Does Mt. Everest really stick up very far? Mt. Everest reaches 8.8 km (5.5 mi.) above sea level. Compare that with the size (average diameter) of the Earth, which is 12,742 km (7,917 mi.). So, the height of Everest is only about 1/1,500 of Earth’s diameter. That’s certainly not much of a deviation from Earth’s (approximately) spherical shape.

Here’s another way to approach this: Say to students, “Suppose we could magically shrink the Earth down to the size of this billiard—or pool—ball.” If you have a billiard ball, hold it up. “If you were to hold this tiny Earth, what would it feel like?” If you feel like throwing them off track, you can add, “Keep in mind that it has all those mountains and valleys and ocean trenches on it. So, what would it feel like? Would it feel rough or smooth?” The answer: If you shrink the Earth down to the size of a billiard ball, it will feel smoother than a billiard ball!

The more massive an object is, the stronger its gravity; and if the object is large enough, gravity will always squeeze it into a roughly spherical shape. In the solar system, any object larger in diameter than about 500 km (about 300 mi.) will be fairly spherical. This includes the Sun, all the planets, the larger moons, and a few of the largest asteroids.

I think it is so cool that we not only know that the Earth is round, but we know why it has to be round. A blind physicist who never heard any evidence of the Earth being round could calculate (using the size and mass of Earth) that gravity will make the Earth approximately spherical.

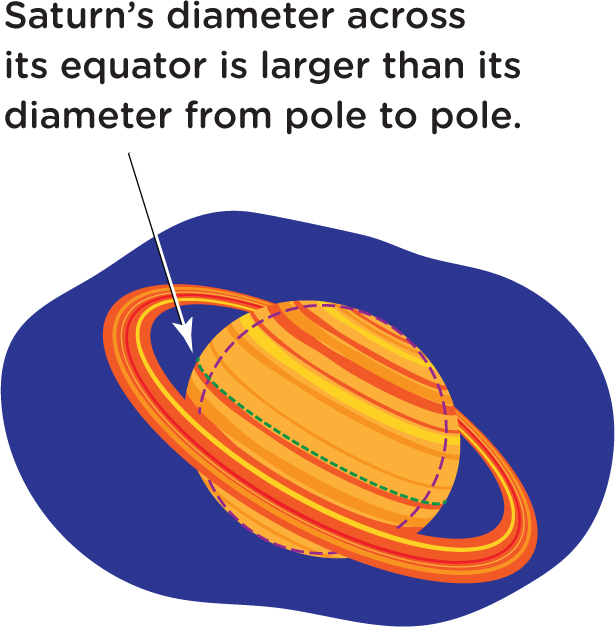
Now, just to round out this article, I should point out the main reason why solar system objects deviate from precise spheres: They’re rotating (spinning). Spinning creates a tendency for an object to spread out (similar to a pizza chef spinning dough in the air) causing it to stretch more, as the outer parts try to fly off in a straight line (in accordance with Newton’s first law of motion). People colloquially call this phenomenon “centrifugal force,” although physicists regard it as a fictitious or inertial force, since there’s nothing really pushing outward (which is why I’m using quotation marks). This “centrifugal force” causes the Earth to bulge out at the equator ever so slightly; it’s a very small effect due to the Earth’s fairly rigid structure combined with its slow rotation. Contrast that with Saturn, which is noticeably flattened due to its faster rotation and its easily deformed gaseous composition. As shown in Figure 6, Saturn’s diameter across its equator is about 10% longer than its diameter from pole to pole.

Finally, just as surface tension pulls a soap bubble into a round shape, the surface tension in water makes water drops somewhat round. So you can see, for example, how rain water beads up into little roundish drops on the hood of your car or how drops of water have a fairly round shape as they roll around in an extremely hot frying pan.

Nature seems to love spheres, so have a ball with this topic!

And never stop learning.

Matt Bobrowsky (DrMatt@ msb-science.com) is the lead author of the NSTA Press book series, Phenomenon-Based Learning: Using Physical Science Gadgets & Gizmos. You can let him know if there’s a science concept that you would like to hear more about.