A: This question applies to many sports and has great appeal to students. It’s also the kind of open-ended question that is perfect for a lesson using Problem-Based Learning (PBL), as it has all the characteristics of a good PBL question:

• It centers on a driving question or problem.
• It’s a non-structured, open-ended problem, with no one correct solution.
• Students require additional information, which they have to find.
• Students decide what they need to know and where they might best find the information. They decide which resources to use (people, books, etc.).
• Students structure their own investigations to develop a better understanding of the concepts.
• Based on this new knowledge, students generate questions, design various solutions, test designs, and work collaboratively toward answers.

Working in groups, students can brainstorm, investigate, and draw conclusions. Getting started is simple: Give each group the driving question and ask them first to plan an investigation to answer the question.

One interesting thing about non-structured problems like this is that different student groups will interpret the problem differently. For example, some groups might focus on the mechanics of how the ball is thrown. Will the ball go a greater distance if it’s thrown underhand, overhand, or sidearm (Figure 1)? Will getting a running start help?

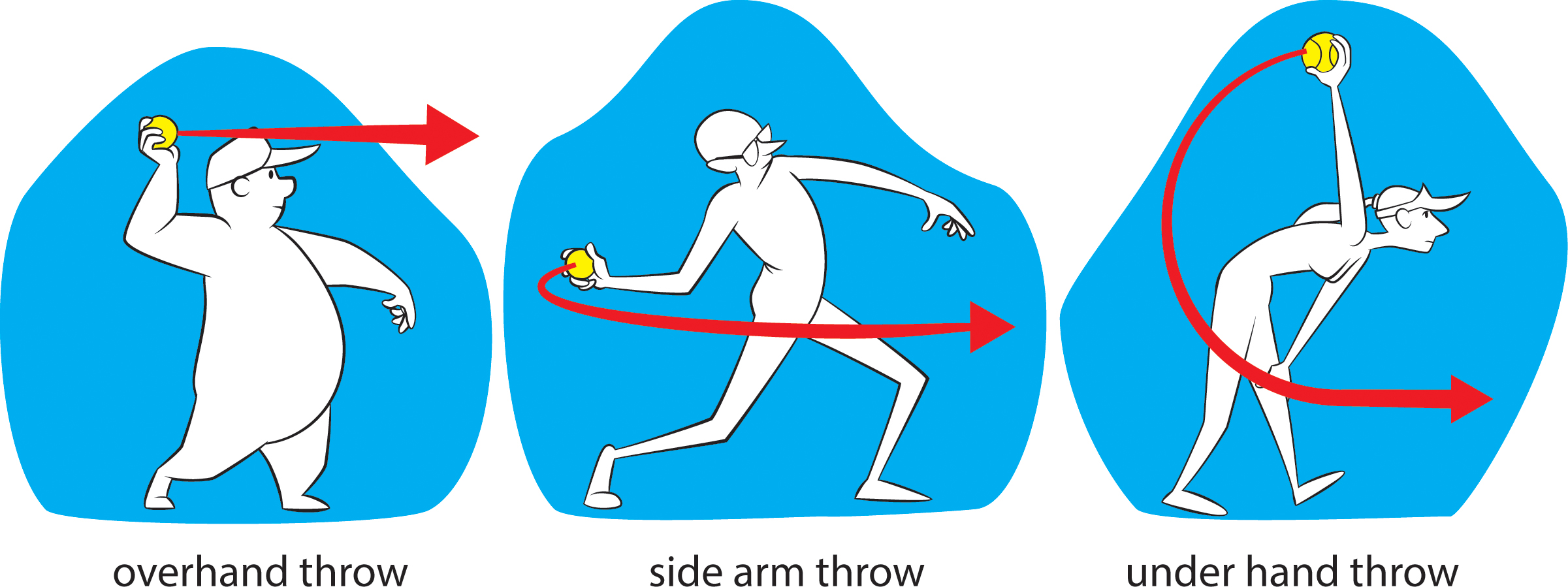
Other groups might look at the direction the ball is thrown. Should the ball be thrown horizontally or at an upward angle? What angle achieves the maximum distance?

Carry out any ball-throwing investigation only in an open field, never inside. Make sure everyone is a safe distance away from where the ball is being thrown.

Regardless of which aspect of the problem students are attacking, there are good scientific practices that they should follow. When they undertake an investigation, they should change only one variable at a time. That’s called a controlled experiment. The reason for having a controlled experiment is that if you change two or more variables and then observe a difference in the distance thrown, it might be hard to tell which variable (or if more than one variable) was responsible for the difference.

Students should also carefully record their measurements and the conditions under which they were made. They should mark the starting point. So that the ball doesn’t go too far, consider using a Wiffle ball. They should repeat each trial (ball throw) more than once, perhaps three to five times. There are several advantages to this. If the ball is thrown a particular way only once, you don’t know if something strange happened, like a sudden gust of wind, which might have made the outcome unreliable. If there are multiple throws, and one outcome is significantly different from the others, students can properly recognize that one as an outlier and possibly decide to ignore it. Also, multiple measurements allow students—if they are up to it—to average the results for a more precise value. And, importantly, students will have a ball (!) seeing how far they can throw.

If students try running forward while throwing the ball, the ball will go faster and farther. This is similar to how a running broad jumper can jump farther than a standing broad jumper. Physics tells us that the ball’s speed will be equal to the running speed plus the speed that the ball is thrown when standing still. The fastest ball speed and farthest distance will therefore come from the student who has both the strongest arm and the fastest running speed. Could this be related to how football players run up to the ball for the kickoff, rather than just standing in front of it and kicking it from a stationary position? (see Figure 2).

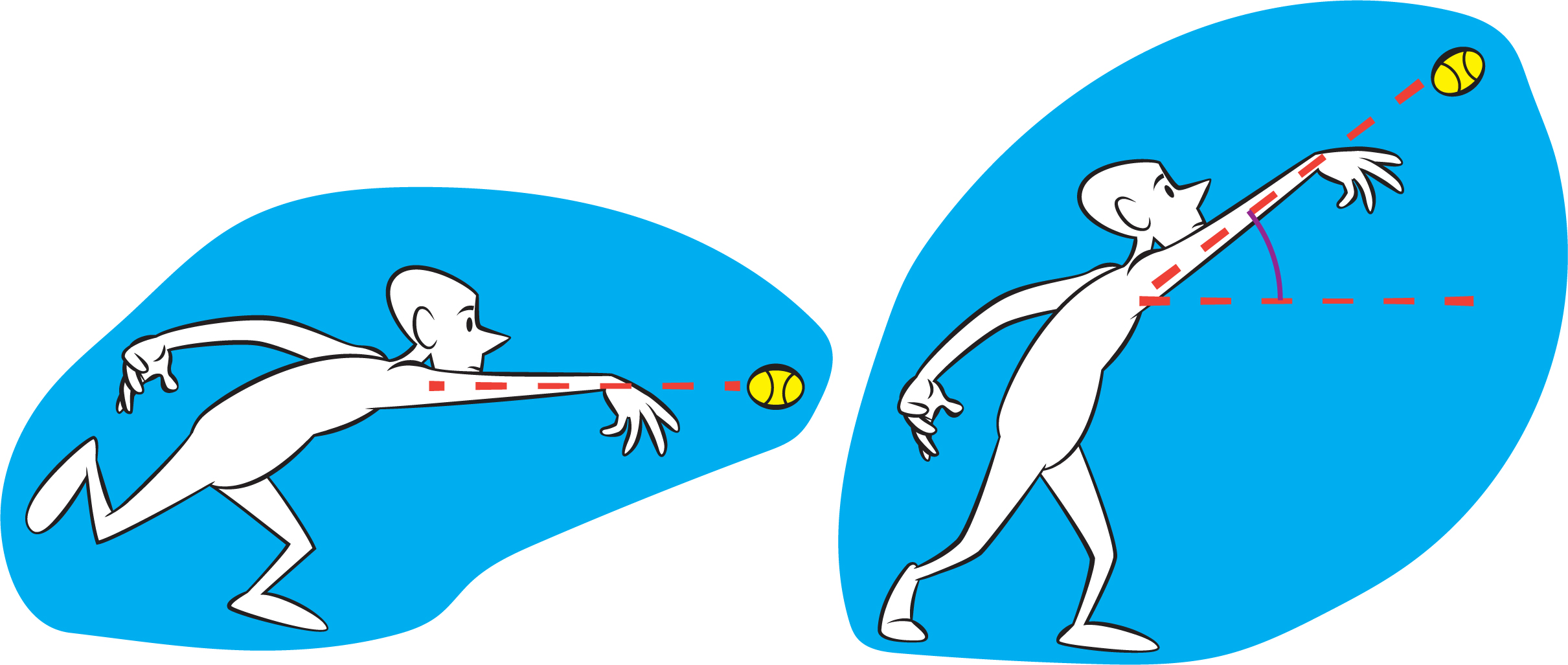
More physics comes into play when determining the correct angle to throw the ball for maximum distance. If you throw the ball too low, perhaps horizontally, then it won’t have far to fall before it hits the ground. On the other hand, if it’s thrown too high—like an infield pop-up in baseball—it won’t go very far either because most of the energy went into making the ball go high, rather than far. (The cartoon at the beginning of the article involves such a high path, or trajectory, for the ball.) So the challenge is to find the optimum angle (measured upward from the horizontal; see Figure 4) to throw the ball. A horizontal throw would have an angle of 0°, and throwing the ball straight up would be an angle of 90°. This is also an opportunity to practice with protractors and learn about angles.

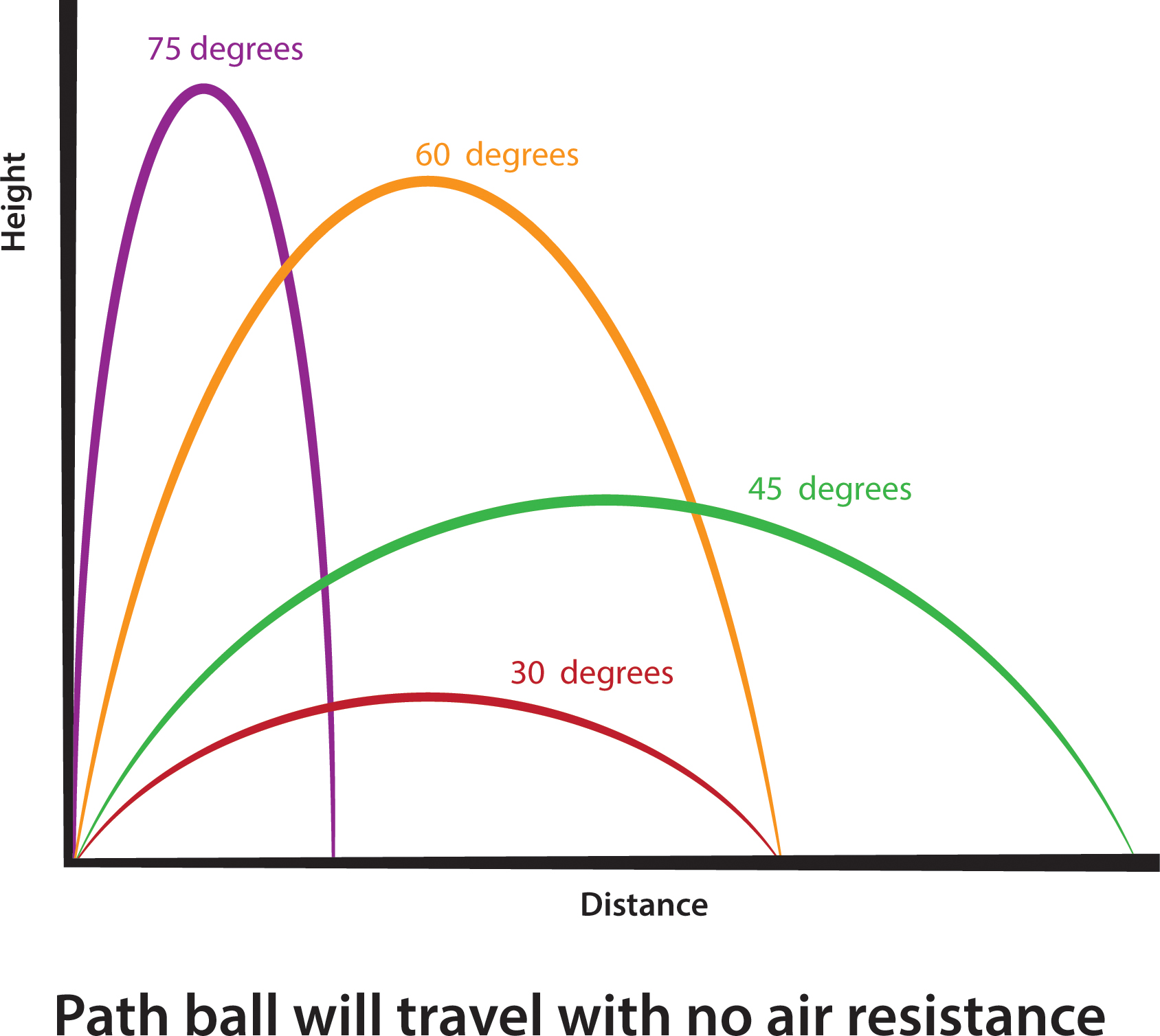
So, at what angle can you throw a ball the farthest distance? That’s actually a more complicated question than it sounds. If there were no air resistance, you would get the maximum distance by throwing at a 45° angle (Figure 3). But there is air resistance, and the faster the ball is thrown, the more air resistance there is. Also, the longer the ball is in the air, the more time there is for air resistance to slow down the ball. That means the farthest throw will come at an angle of less than 45° so that the ball isn’t in the air as long and therefore doesn’t lose as much energy due to air resistance. To be precise, the angle for maximum distance actually depends on how fast the ball is thrown, so it’s perfectly reasonable for different students to come to different conclusions about the best angle.

Students might find it difficult to measure the angle at which the ball is thrown. One approach is to make a video of the ball being thrown and analyze the frame of the video just after the ball leaves the student’s hand in order to determine the angle (see Figure 4). An extension for groups that finish sooner than the others is to ask them if they can give the ball some spin as they throw it and see if that makes a difference. And they can investigate whether the way to throw for maximum distance is different for different kinds of balls.

The ball-throwing investigation can be followed up by a related activity with the teacher launching an air rocket at different angles while students predict and then measure which angle made the rocket go farthest (see Figure 5). There are many places to get simple, air-powered rockets (see Internet Resource).

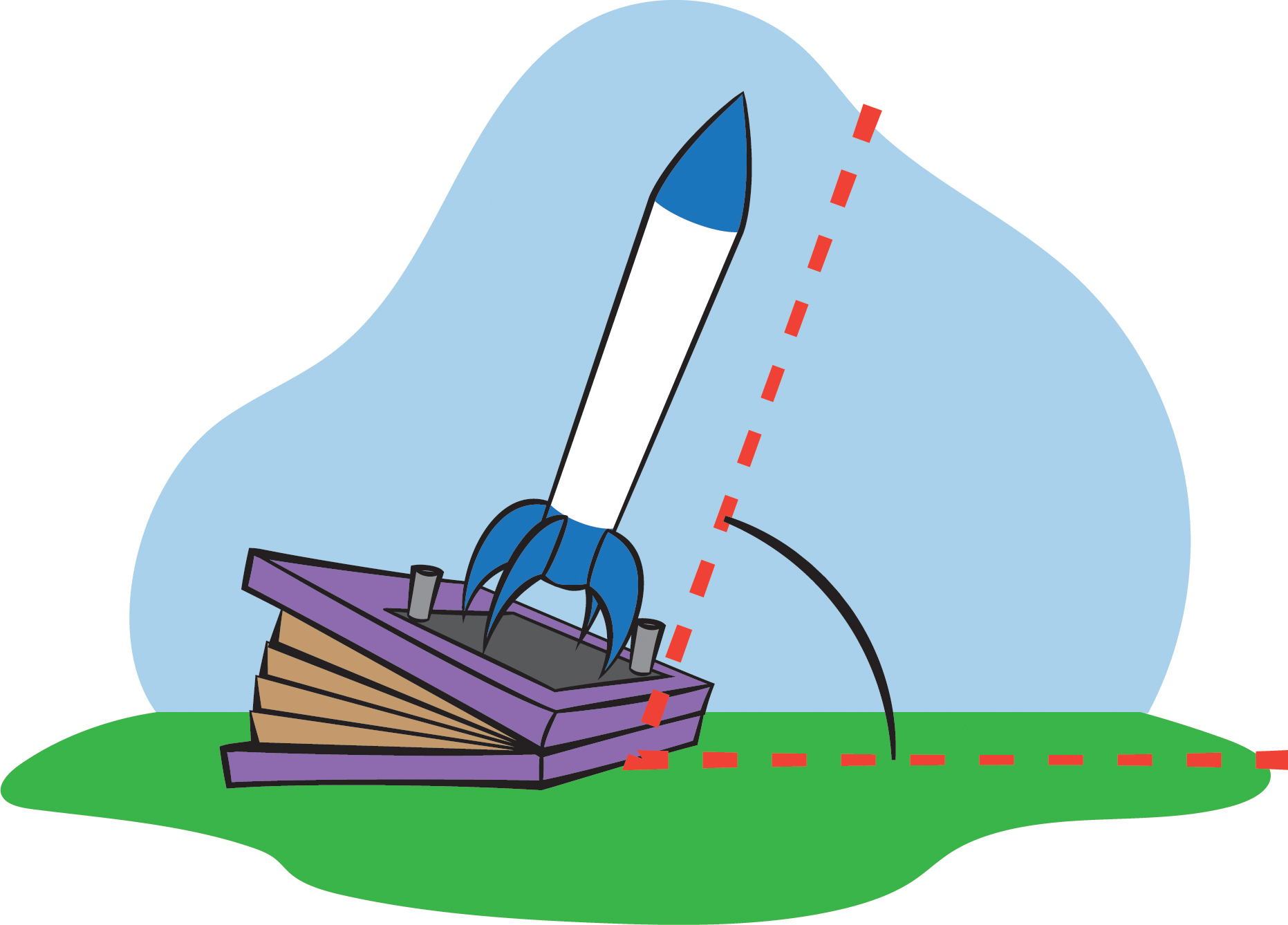
Safety glasses are required for anyone operating the rocket or standing nearby. Carry out this investigation only in an open field, never inside. Before launching the rocket, make sure everyone is at a safe distance. Never stand over or close to the rocket while it is being pressurized or launched.

Problem-based learning (discussed in this issue) and phenomenon-based learning (discussed in the September 2018 Science 101 column) are open-ended and allow students a lot of latitude in how they explore and learn. If I had given you a set, step-by-step procedure for students to follow, that wouldn’t be PBL. And it wouldn’t be science.

Never stop learning!

INTERNET RESOURCE
Air Powered Projectile Group www.arborsci.com/air-poweredprojectile-926.html