A: There are some concepts that are hard to define, even though we have a great intuitive feeling for what they are. Energy is one example. You probably have a good feeling for what energy is. You know it when you see it. And yet it’s difficult to define. Another easy-to-picture but difficult-to-define concept is waves. Here’s one attempt at a definition: Waves are regular patterns of motion, which move, or propagate, through some substance, like air or water—or anything. Light waves are a special case, which can also move through empty space. Much of what follows doesn’t apply to light waves, but I’ll say a few words about light later on. One other key point, which you’ll see illustrated in the examples: Waves transfer energy, not matter. Matter doesn’t move along with a wave, but the energy in the wave does move along.

To make a wave, you just need to make a little disturbance in some substance. It’s easy to see waves in water, so you can start by taking the largest (i.e., widest) pan or bowl you can find, putting some water in it, and then dropping in a small object, like a pebble, which will jostle, or “disturb” the water where it falls in. Students can do this in school or at home and watch the waves propagate outward from the source of the disturbance. At home, students can explore waves in a bathtub as well. Tapping the water at one end will send waves down to the other end. You can also ask students whether they observe that a wave reflects off the end of the container (or bathtub) and starts to come back.

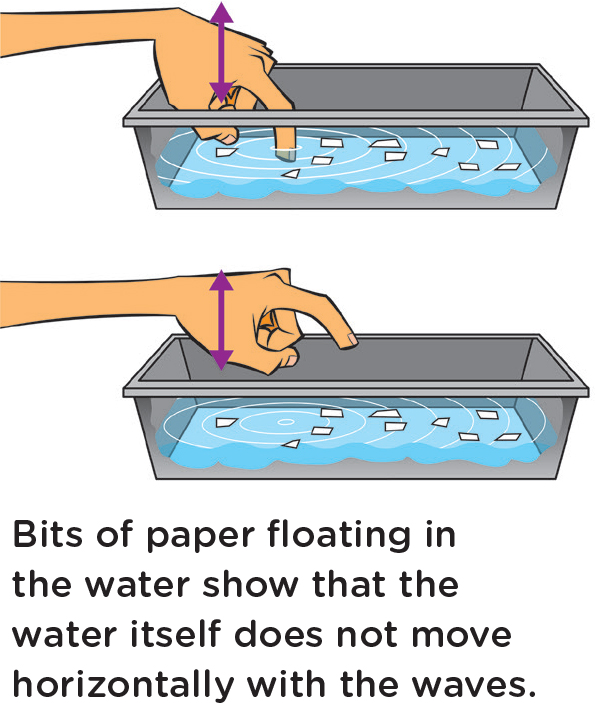
Now that they’ve seen the waves move along, ask students whether water is flowing outward from where the water was initially disturbed. In other words, is the water moving along (horizontally) with the waves? To check this, they can drop some bits of paper onto the water (see Figure 1). This time, they can make a continuous series of waves by repeatedly tapping a finger or dunking a hand in the water. If they do this rapidly, as though they’re keeping time to some fast-paced music, they’ll get a nice series of waves traveling along. Do the pieces of paper travel with the waves? No! So the water itself is not moving from one end to the other. The bits of paper show that the water moves up and down but does not travel along with the waves. You can see the same phenomenon if you put some rubber duckies in a bathtub. The duckies bob up and down, but do not move along with the waves. (An exception, when water does move along with a wave, occurs when the water is very shallow, as when waves break on a beach.)

Of course, water can move horizontally, and we call that a current. The waves might be moving in a different direction from the current. For example, the water might be moving north with a current, while a wind from the west makes waves moving east.

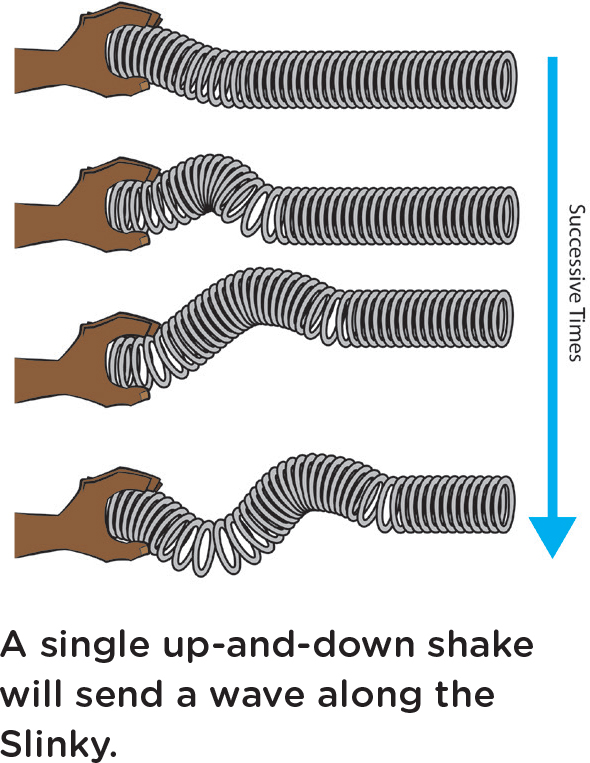
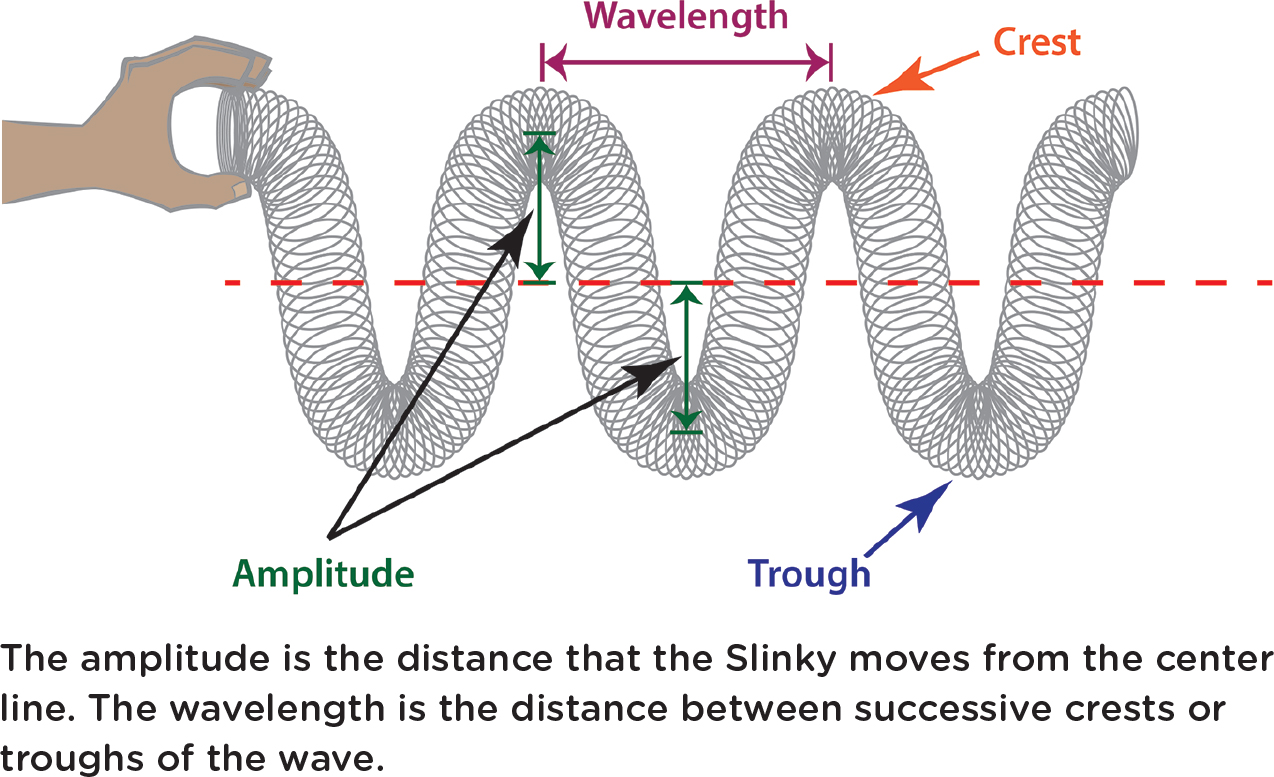
Another way to easily make waves—and see waves—is to stretch a Slinky out and shake one end up and down. Just a single up-and-down motion will send a wave down the slinky (see Figure 2). Again, it can be seen to reflect back. Repeated up-and-down motions will produce a series of waves. Students can easily see these waves move and see that there is a certain distance between successive crests (or troughs) of the wave. That distance is called the wavelength. We can again ask whether the Slinky material moves along with the waves as they travel from one end to the other. Tie a small piece of string to the middle of the Slinky and then make waves, and you’ll see that the coils themselves don’t move from one end to the other. This is a general property of all types of waves in all types of materials: The material itself only shakes, or vibrates, but doesn’t move along with the waves. This should help make it clear that a wave arises when one part of some material starts shaking, which causes the material next to it to shake, which causes the material next to it to shake, and so on. The shaking moves along throughout the material, and we call this a wave.

We’ve looked at two kinds of material so far—water and a (plastic or metal) Slinky. But the same process can make waves in many types of material—from the string on a guitar to the sound waves in air. If you have read the April 2019 Science 101 column, you know that sound waves are a different kind of wave—a compression wave, where the air repeatedly gets squeezed, or compressed, and then expands. The April 2019 article also showed how to make compression waves with a Slinky.

Just how much the material moves as it shakes is called the amplitude of the wave. For example, in the case of the Slinky (Figure 3), the amplitude of the wave is the distance from the center line (i.e., where the Slinky would be resting if there were no waves) to the top of the crest or to the bottom of the trough. It takes more energy to make a higher-amplitude wave. That makes sense, since you have to shake the Slinky harder to create the greater amplitude.

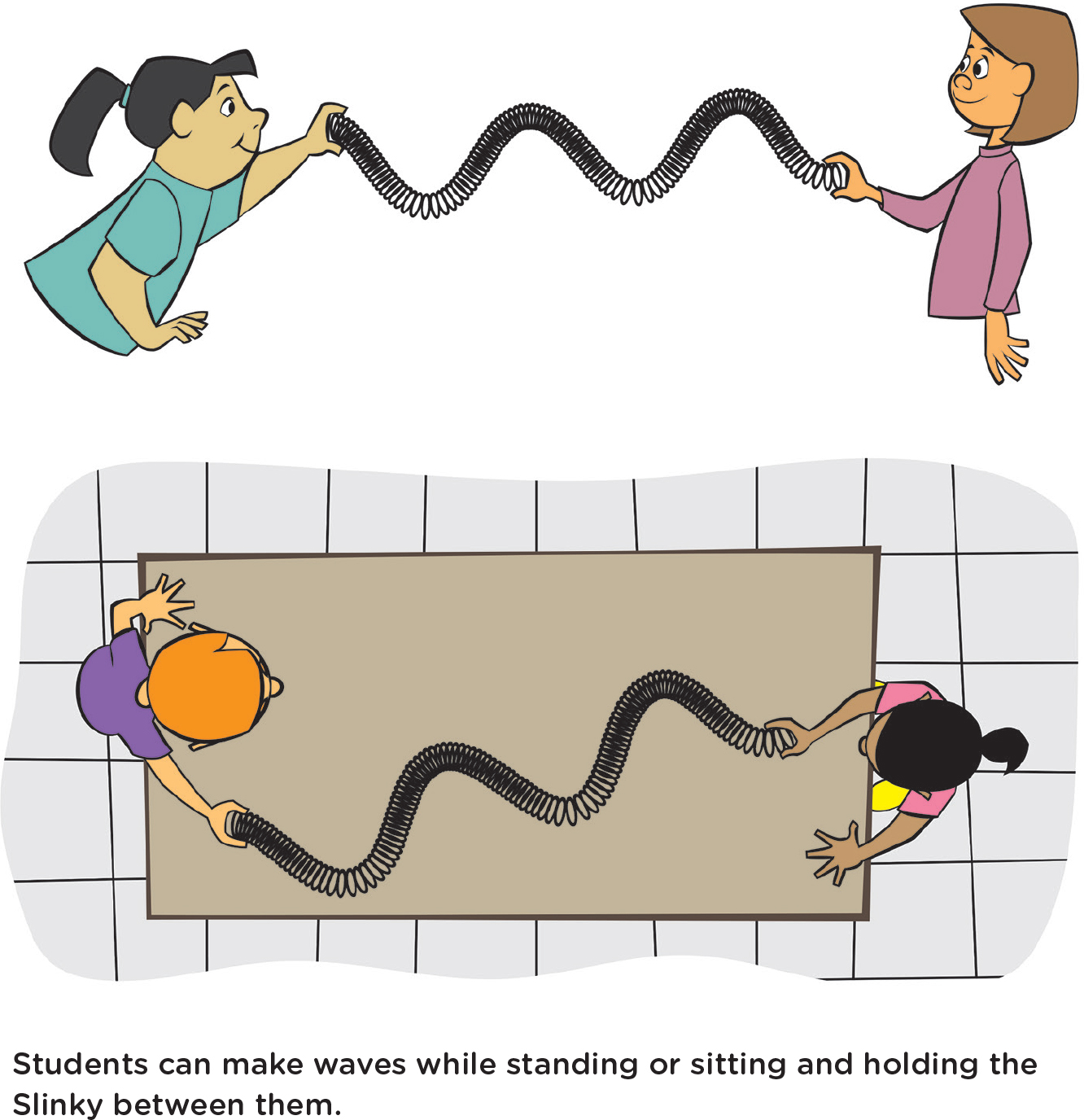
So now we have a new idea: Waves carry energy. If two students hold a Slinky between them, and one of them starts making high-amplitude waves, the other student can feel the tug from those waves. That tug demonstrates that energy has been transferred from one student to the other by the waves. (Two students can make slinky waves either vertically while standing up or horizontally on a long table or on a floor; see Figure 4. While standing, one student holds the end of the Slinky still while the other student shakes the end up and down. On the floor or table, one student shakes the end of the Slinky from side to side.) Sound waves also carry energy, and students can see an example of sound waves breaking glass by following the link in the Internet Resources at the end of this article. The video also shows how the glass vibrates from the sound waves. Did you see how much the glass can bend before it breaks?! I find that amazing. As the glass flexes and vibrates, the amount that the glass moves is the amplitude of the vibration. When the amplitude gets high enough, the glass can’t bend any further without breaking, which it does.

Another way students can tell that waves carry energy is by using a microwave oven. The microwaves, which are short-wavelength radio waves, deposit their energy in the food, increasing the heat energy there. (It’s because the food is heated using microwaves that we call it a microwave oven—in the same way that food can be heated by solar radiation in a solar oven.) Challenge students to think of other places where they can see that waves carry energy. Some answers might include how ocean waves can make a boat rock to and fro and can even cause a boat to tip over (capsize); standing out in the Sun, you can feel how the radiation from the Sun (mostly infrared and visible light waves) make you warmer—or how that same radiation will be absorbed by solar cells or solar panels to produce electrical and heat energy; compression waves in the air from a nearby explosion can break windows; and sound waves can make matter vibrate.

One last thing about waves that is very interesting is that waves can carry information. Information travels to and from cell phones using radio waves or microwaves. Radio and television stations broadcast programs using radio waves. Sound waves carry information to your ears, which, in turn, send that information to your brain. Similarly, light waves carry information to your eyes, which, in turn, send that information to your brain. Astronomers learn enormous amounts of information about planets, stars, and galaxies by analyzing the light waves emitted by those objects. (I’ll have more to say about waves carrying information in a future Science and Children issue devoted to information processing.)

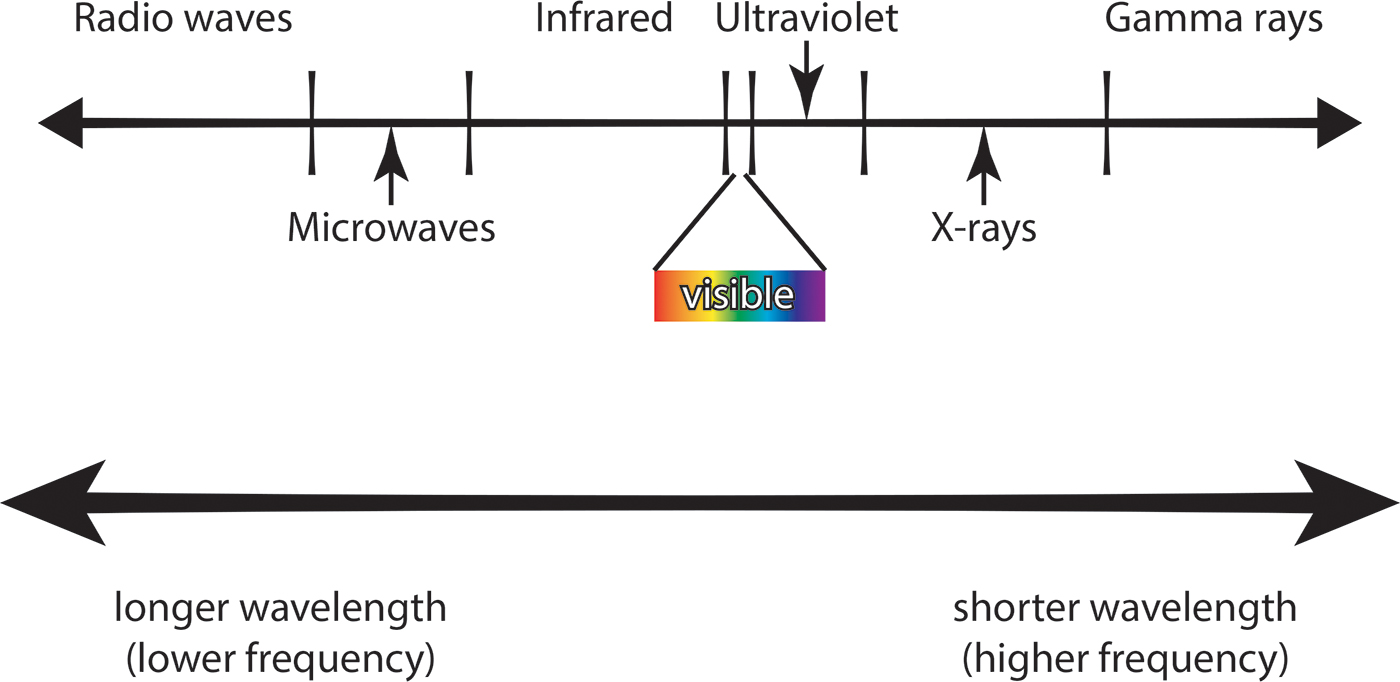
If I mention light, most people immediately think of visible light. But there are also invisible forms of light. All these kinds of light—both visible and invisible—comprise what scientists call the electromagnetic spectrum. The word electromagnetic is there because light actually consists of traveling electric and magnetic fields. The electromagnetic spectrum includes the following kinds of waves: radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, × rays, and gamma rays (see Figure 5). Our eyes are sensitive only to the very narrow band of visible light, but all those other kinds of radiation are the same kind of thing as visible light, only with different wavelengths. Light waves are different from other kinds of waves because, while other waves need some material to travel through, light waves can travel through a vacuum. You know this because you can see the light from the Sun and other stars—light that has traveled through the vacuum of space. And that’s true for all electromagnetic radiation. So, for instance, radio waves can also travel through the vacuum of space. (Long ago, I carried out research that involved studying radio waves emitted by the Sun.)

Check out the University of Colorado’s PhET wave simulation for wave activities that students can do from their computers wherever they are (see Internet Resources).

Finally, do you know what physicists enjoy doing the most at sporting events?

The Wave!

Never stop learning.

Internet Resources

Sound breaking glass

https://techtv.mit.edu/videos/2964-breaking-glass-with-sound

Wave simulations

https://phet.colorado.edu/en/simulation/wave-on-a-string 

Matt Bobrowsky is the lead author of the NSTA Press book series, Phenomenon-Based Learning: Using Physical Science Gadgets & Gizmos. You can let him know if there’s a science concept that you would like to hear more about. Contact him at DrMatt@msb-science.com