Focus on Physics
Measuring Shadows to Calculate the Size of Earth
The Science Teacher—February 2020 (Volume 87, Issue 6)
By Paul G. Hewitt
In the September 2016 issue of The Science Teacher, my article “When Our Round Earth Was First Measured” told of the great achievement of the Greek scholar Eratosthenes in calculating Earth’s size around 240 BC. In this article I expand on this achievement and show how Earth’s circumference can be calculated by measuring the shadows cast by any pair of sunlit vertical structures a known distance apart. A meterstick and a smartphone are all that is needed.
Great circles
A great circle is the largest possible circle that can be drawn around a sphere. Through any two points on a sphere such as Earth, no matter the direction of the line separating them, a great circle can be defined and drawn. Commonly charted great circles are Earth’s lines of longitude, all passing through the north and south poles. Only one great circle lies along a line of latitude, that of the equator. But there are an infinite number of great circles about Earth, all with their centers at Earth’s center (Figure 1).
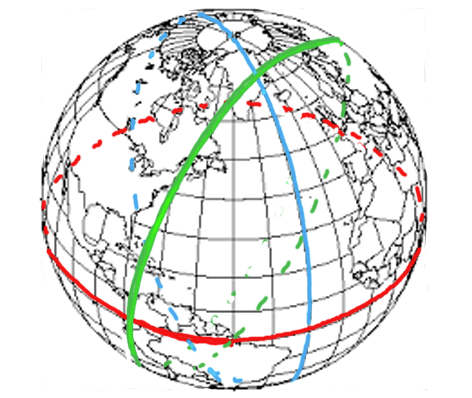
Three great circles: red at the equator, blue along a line of longitude, green in a random direction
Like any circle, the circumference of a great circle can be divided into 360°. This means, for example, if the surface distance between any two points along the circle is subtended by 1°, then the circumference of the circle is 360 times that distance. The same is true for other angles.

Eratosthenes
Eratosthenes was able to calculate Earth’s circumference because he knew both the distance between two cities along a great circle (800 km in today’s unit of measurement) and the subtending 7.2° angle of that distance. Since 7.2° is 1/50 of a circle, the circumference of planet Earth is simply 50 times the distance between Alexandria and Syene—50 x 800 km (Figure 2). That’s 40,000 km, quite close to today’s measured value of 40,008 km.
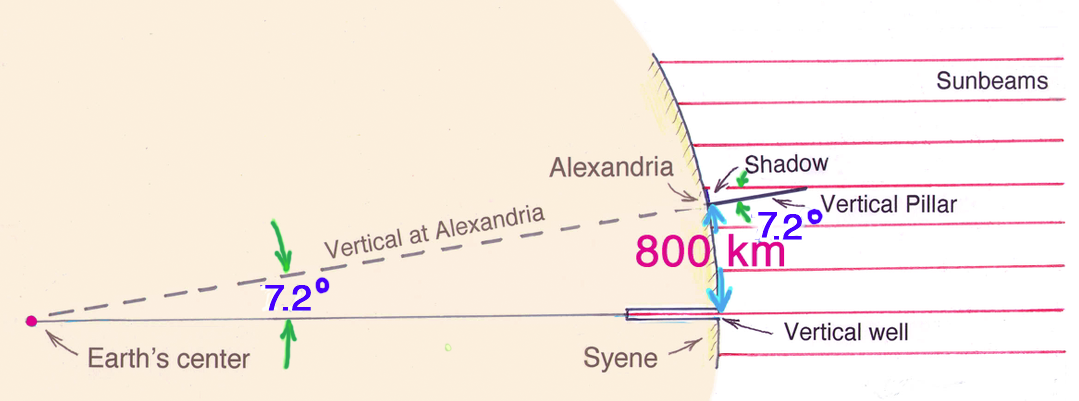
A 7.2° angle is subtended by the 800 km arc between Alexandria and Syene
Beyond Eratosthenes
Because the path from Alexandria to Syene lies very close to a line of longitude, it might be imagined that a condition for Eratosthenes’ deduction had to involve a line of longitude—not so! Any of Earth’s great circles, in any orientation, lend themselves to a calculation of Earth’s circumference. The calculation involves only simple trigonometry when the sunbeams striking a great circle lie in the plane of that circle. Otherwise, more complex spherical trigonometry must be employed (Mungan 2019).
Tree shadows
In the simpler case where the sunbeams strike a great circle in its plane, the vertex angle at Earth’s center relates directly to the angles of sunbeams at Earth’s surface. Consider the pair of widely-spaced trees bathed in sunlight shown in Figure 3. Shadows of the trees lie along their great circle, as evidenced by the shadow of the lower tree pointing directly to the upper tree. Imaginary vertical extensions beneath the trees meet at Earth’s center. In this case they form a vertex of 10°. Why 10°? Because the shadows are in the same plane as the great circle, 30°— 20° = 10°.
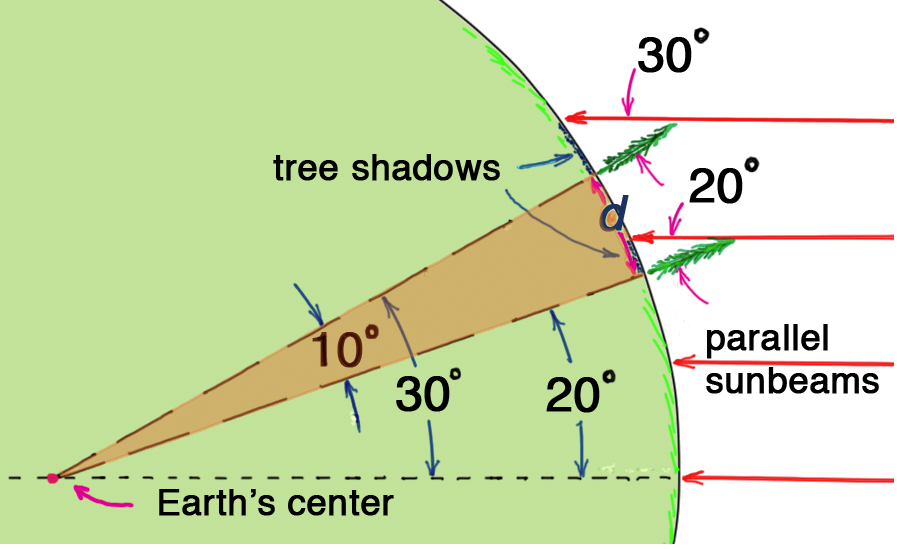
The two-tree arc d subtends an angle of 10° at Earth’s center.
How many 10° segments of Earth make up a full 360° circumference of Earth? The answer is 360°/10° = 36. This tells us that Earth’s circumference is simply equal to 36 times the distance between the pair of trees! When the shadows of two vertical structures point toward or away from each other, the size of Earth can readily be calculated. Mission accomplished!
Working backward with our 30° and 20° angles of sunbeams, and knowing Earth’s circumference to be about 40,000 km, the trees would have to be some 1,100 km apart (40,000 km/36). In practice, one would want to work with trees closer together. At 110 km apart, the arc distance between them would subtend a 1° angle at Earth’s center.
School flagpoles
Trees are not alone in casting well-defined shadows. Whether tall or short, all vertical structures in sunlight cast shadows. And for far-apart cities where the separation distances are known quantities, an interesting student exercise is applying the pair-of-trees idea to shadow-casting flagpoles at their schools.
Anywhere on the globe, with rare exceptions, the shadows of a pair of vertical structures in sunlight will align along a great circle at some time on some day. To calculate Earth’s circumference as discussed above, a team of students must find a date and time when the shadow cast by their school flagpole points directly toward or directly away from the flagpole of a cooperating team in another city.
If the Sun is shining in that other city, shadows there will meet the same criterion at the same time. If the day is cloudy or rainy, or if it’s a weekend, be patient: Very nearly the same conditions will apply for several days running.
Student investigators in both cities can use compasses to tell when the shadows cast are aligned (the first pointing toward the second and the second away from the first—or, in the special case where the Sun is directly above a point between the locations, each pointing away from the other). This information may also be found on the internet.
The synchronized timing that was a problem for Eratosthenes is not a problem today, for every student and every teacher can access accurate time on a smartphone or other device.
The difference in the two measured angles (or, if the shadows point away from each other, the sum) equals the angle at the vertex at Earth’s center where extended vertical lines of each flagpole intersect (Figure 4). With good data, estimates of the circumference of Earth can be calculated.
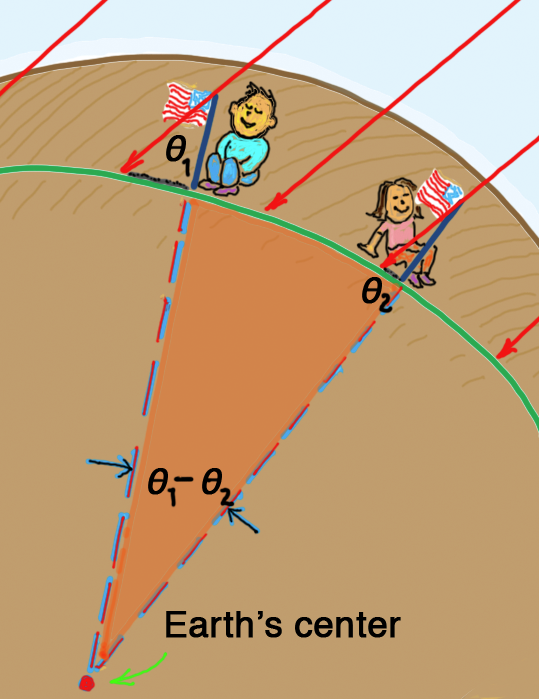
Angular difference θ1 – θ2 = Earth’s vertex.
Or consider doing the reverse: Use Earth’s 40,000 km circumference as the known value, and find the unknown distance between far-apart flagpoles. Either way, this can be an engaging and exciting school activity.
Mathematics Physics High School


