Feature
For Your Eyes Only
Introducing Quantum Key Distribution to High School Students
The Science Teacher—January/February 2021 (Volume 88, Issue 3)
By Zeynep Gonca Akdemir, Muhsin Menekse, Mahdi Hosseini, Arindam Nandi, and Keiichiro Furuya

Quantum technologies refer to any technology developed based on the principles of quantum physics. Quantum communication, quantum computing, and quantum sensing are applications of such technologies, in which quantum mechanics underpins the key assumptions on their design and development. Quantum technologies promise revolutionary and disruptive innovations across a wide range of industries. Quantum computing will play an important role in artificial intelligence and will have an impact on every sector of the economy, from healthcare to national security. Currently, the workforce possessing a fundamental understanding of, and the technical skills needed for, quantum technologies is limited.
This situation creates a significant challenge for our educational system to address. We need to attract young people from diverse backgrounds to become engineers and scientists trained in quantum technologies. However, teaching a counterintuitive concept such as quantum cryptography might confuse young learners. Quantum cryptography is disconnected from physical realities that students expect to observe. Due to its nontrivial and counterintuitive aspects, it should be taught based on conceptual ideas rather than complex mathematical formulizations (Krijtenburg-Lewerissa, Brinkman, and van Joolingen, 2017).
In this article, we demonstrate how to conduct an experiment with a quantum cryptography demonstration kit (Thorlabs 2017) and then provide a sample lesson plan about quantum key distribution (QKD), which illustrates the distribution of a key (or password) to encrypt or decrypt messages with the use of quantum properties based on the BB84 protocol developed by Bennett and Brassard (1984; 2014).
We used the inquiry-based learning cycle (including the phases of exploration, concept introduction, and concept application) offered by Unruh, Countryman, and Cooney (1992) for the full lesson, and taught it over three 50-minute class periods, culminating in the quantum key distribution experiment detailed below. The first period introduced the phenomenon of wave-particle duality and its relation to quantum particles and the Einstein-Bohr debate, the relation between the wavelike probability of electrons, and the Heisenberg uncertainty principle. The second period examined quantum superposition, the phenomenon of quantum entanglement, the properties of quantum particles (namely photons), quantum computers, and secure information technology. The final period focused on quantum cryptography and featured the quantum key distribution activity.
Differentiation strategies
We developed several options to meet the needs of students with individualized education plans (IEP):
- Provide a navigating manual with colored pictures and figures for students who may struggle with verbal or written directions.
- Fill in notes with laminated/colored paper to help students who may struggle to focus on the experimentation.
- Revise worksheets with matching items instead of blanks, and use diagrams with word banks or color coding.
- Provide slides with screenshots of the directions and questions.
- Showing pre-recorded short videos of the experiment to help students understand the setup.
Day 1
The guiding question for Day 1 is: Is it possible for a matter to be in both wave nature and particle nature? Start with a discussion called “The Bohr-Einstein Debate.” Divide the class into groups representing Bohr and Einstein, assign one claim (Bohr: entities, such as electrons, had only probabilities if they weren’t observed; Einstein: electrons have independent reality and have a spooky action at a distance) to each group, and ask each group to collect evidence from online resources within 20 minutes. Set the timer to five minutes for each group to justify their claims based on evidence. Provide opportunities for each group to ask questions to better understand their evidence-based data collection procedures. This 10-minute session will help them demonstrate their proficiency in asking topic-relevant questions to their peers, and improve their scientific evaluation skills.
Ask students to focus on phenomena that Newton’s laws can describe and predict, as well as the limitations of classical mechanics. See Online Connections for video links that can be used to prepare students before performing the quantum key distribution activity.
To finish the first day, have students ask their own questions regarding the phenomenon introduced. Ask them to think about “How could The Bohr-Einstein Debate contribute to the development of the technologies used in the 21st century?” and encourage them to create their own questions about quantum technologies, the use of coding, and the development of novel super-fast computers that also send secure information to other parties.
Day 2
We begin with discussion questions for the day’s activities:
- What is the probability of getting heads or tails when you flip/toss a coin?
- Is it possible for an object to exist in two places at the same time?
Provide each student with a coin. Ask them to flip their coins and observe which state each coin possesses while it is flipping. Ask students to think about the rationale of this activity and explain the relationship between coin analogy and wave–particle duality in quantum mechanics. Mention the phase of a coin toss when we can see neither heads or tails. Then, point out the similarity between this analogy and photons, which hide their states and show several probabilities. Describe how a quantum particle like a photon or an electron can also have “head” or “tail” states defined by their direction of oscillation or energies. We have used videos to help students make sense of the hiding states of photons (see Online Connections).
Next, prepare two cards showing two distinct shapes (like a circle and a star) before the lesson and copy those cards based on the number of the students attending in this class. Provide each student with two cards and ask them the following questions based on the two probability cases:
- Independent: Objects shown in the cards have the shape of either a circle or a star with equal probability. Let’s say those two objects are independent, what could be the chance of finding one of the four pairs?
- Entangled: Let’s assume the two objects are entangled. What would be the probability of each type of the pair in that case?
Figure 1 shows an idealized example of entangled objects to check students’ accurate responses.
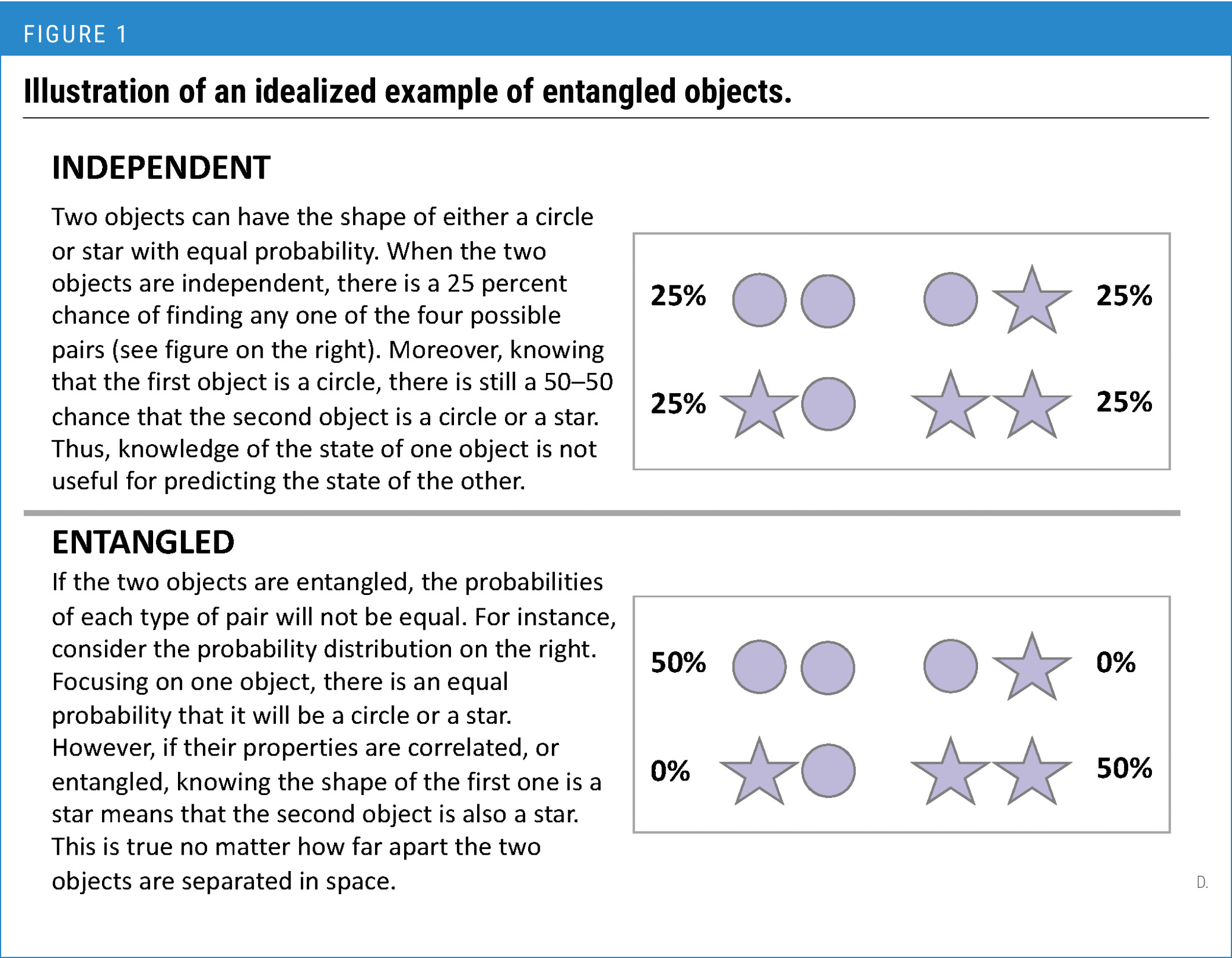
Illustration of an idealized example of entangled objects.
Ask students to research quantum entanglement online (10 minutes) and summarize their findings. Let them explore and engage in a small scientific research experience in which they will be evaluating their claims, evidence, and reasoning based on the phenomenon of quantum entanglement. This will help students create their own predictions about the phenomenon before the instructors’ actual explanation. Provide them with the following guiding questions to facilitate their investigation about quantum entanglement and let students think about these questions and discuss their answers within a think-pair share activity set in 10 minutes:
- How do you explain quantum entanglement?
- What are some possible applications of quantum entanglement?
After getting the students’ predictions, show the video “Quantum Entanglement | Einstein’s Quantum Riddle” (see Online Connections) and ask them to think about some real-world examples of how the functionality of quantum entanglement can make our daily lives easier.
Share the following information to consider before the next class period: Scientists can engineer photons or electrons as quantum bits (qubits) showing wave–particle duality. Quantum computers use many qubits, some entangled, to perform simultaneous computation tasks, thus speeding up the process. Using individual or entangled photons, scientists can encode and transmit information that is fundamentally unhackable. This is because quantum information cannot be copied. Quantum cryptography and quantum communication are branches of quantum information science focusing on secure information transfer between parties. Finally, ask students to envision the best way to keep a hidden message secret with all of the new technology available.
Day 3
The guiding question for the final day of the lesson is: How is a secure key generated between two parties with photon sources for reliable transfer of information? Use think-pair-share approach for students to participate in the discussion. Allow students to share their ideas without providing them feedback or instruction. After 10 minutes show the “Quantum Confidential” video (with sound turned OFF) and ask students to think about the following questions while watching it:
- How would you narrate this video?
- How would you put the roles of each figure in the video?
- What could be the message sent?
- What do you think about the numbers in the folder? What would they represent?
Based on the questions, let students discuss their own narration for 10 minutes as pairs and ask them to generate three possible concepts based on their guiding questions related to this content. Let students have a talk in pairs. Then, turn on the video again with sound ON and ask them to check their predictions.
Next, introduce the simulation that will help students conceptualize how secure information processes are maintained through Quantum Key Distribution (QKD). Discuss the application of quantum entanglement on quantum computers by referring to a two-state quantum-mechanical system or qubit. Then, introduce the roles of Alice, Bob, and Eve, and remind students that this activity will be limited to working on Alice and Bob (not Eve) to conceptualize how key generation between Alice and Bob occurs.
Quantum Key Distribution (QKD) Activity
QKD is a secure method of distributing a key between parties to encode and decode un-hackable messages. The principles of quantum physics assure the security of information. It is conducted by three hypothetical nodes: Alice, Bob, and Eve. Alice is the sender of the secret key and sends polarized single-like photons to Bob. Bob, equipped with a polarizing analyzer and a pair of photon detectors, receives the bits corresponding to the key, and then Alice and Bob publicly communicate to decide on the secure key. The purpose of this communication process is to ensure that no third party (e.g., called Eve (eavesdropper) in this experiment) can have access to the key.
The key distribution process in this activity relies on the BB84 protocol, in which single photons carry bits of information in specific polarization states. The uncertainty in knowing the polarization state prepared randomly by Alice makes it impossible for an eavesdropper to copy information without being detected. As Bob also does not know the polarization states of photons sent by Alice, he chooses a random polarization basis to carry measurement. At the end of the process, Alice and Bob publicly share the polarization coordinates (basis) used for preparation and detection, but not the result of measurements.
Only the result of measurements for bits where the same polarization basis used by Alice and Bob are kept, and the key is then generated. It can be shown that in the presence of Eve, the interception attack can be detected by sharing a small portion of the key. The key is determined to be secure when the probability of error in that portion of the key is less than 25%. The node where eavesdropper or Eve intercepts is shown in Figure 2.

Parts of a quantum cryptography demonstration kit (EDU – QCRY1).
Instructions for Alice
1.Randomly generate and enter a basis (+ or x) and a bit (0 or 1) for each of the 52 bytes and record on the byte chart (Table 1).
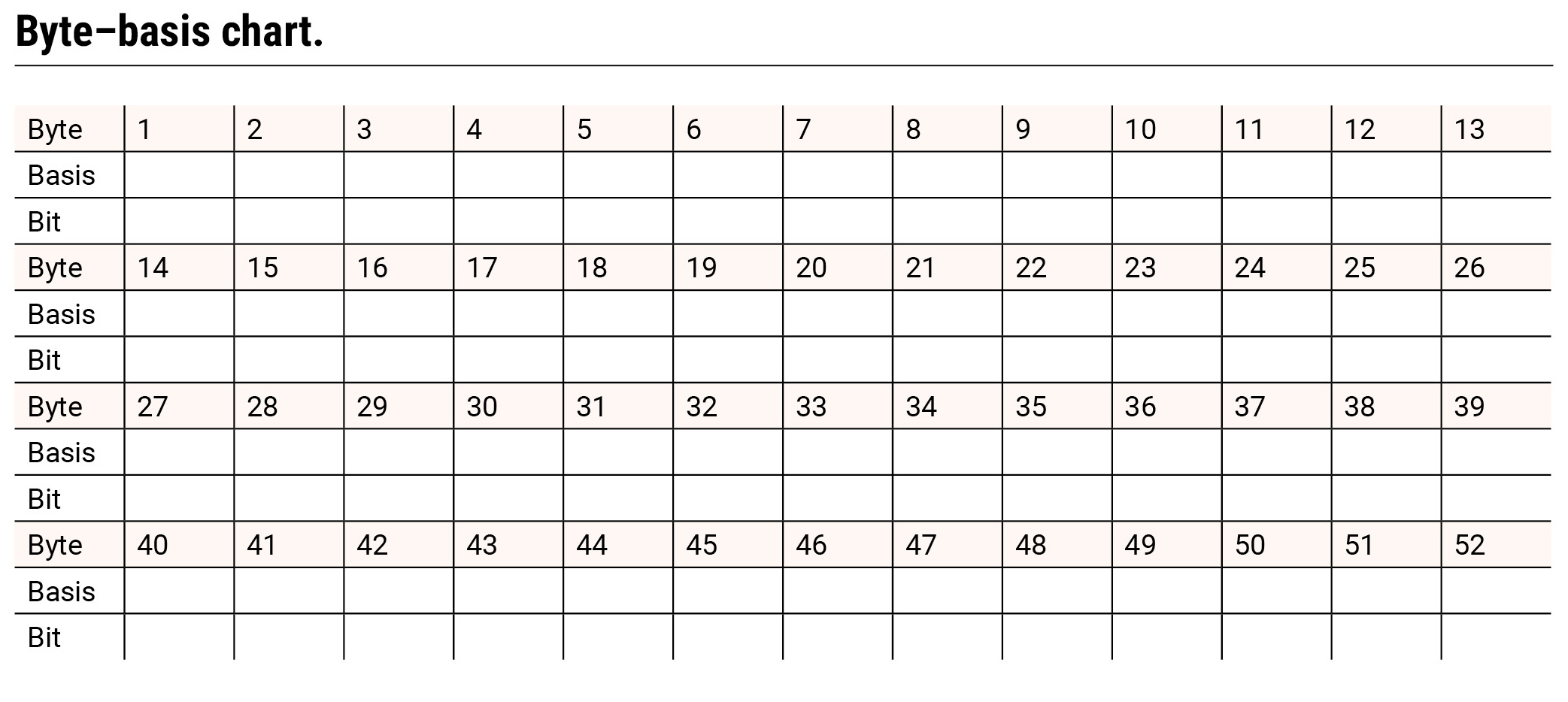
Byte–basis chart.
2.To transmit this information, set the polarizer dial to the correct basis for byte 1.
3.Callout “sending byte [insert number] and press the red button. Repeat steps 4 and 5 through byte 52.
4.Bob will give you his basis for each byte to compare. Circle those bytes that match. (If basis does not match, disregard that byte.)
5.Record the first 20 circled bits in order from the matched basis to generate the key (key bit)
6.Complete Table 2 to prepare and share your encrypted message.
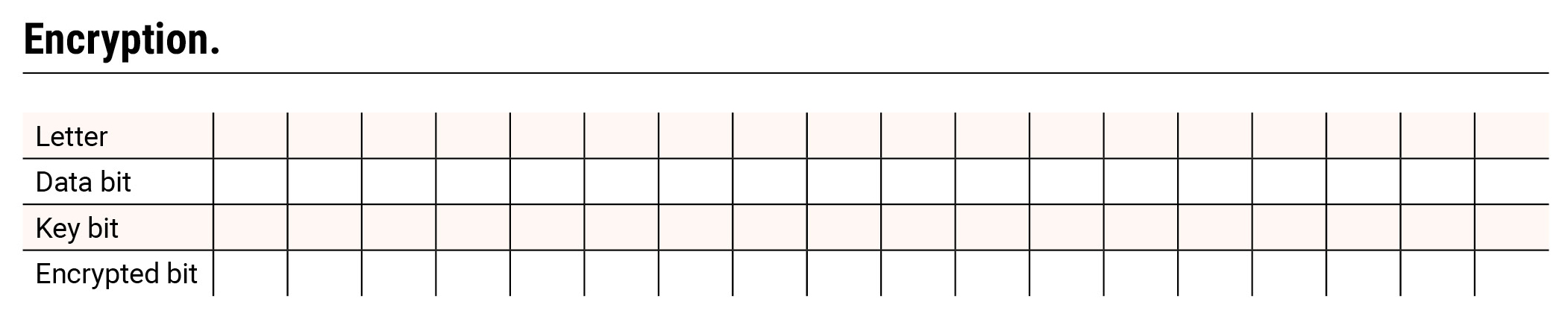
Encryption
- Enter a four-letter word (i.e., hide) in the top row (letter).
- Translate each letter into binary code (data bit).
- Combine the data bit and the key bit for each column using the “calculation rules” for binary addition creating the encrypted bit.
- Share your encrypted bits with Bob.
Instructions for Bob
- Randomly generate and enter a basis (+ or x) for each of the 52 bytes and record on the byte chart (Table 1).
- Set the polarizer dial to the correct basis for bit 1.
- Callout “receiving byte [insert number].”
- If the detector is directly in front of polarizer lights, record a 0 as the bit, and if the detector is at 90º light, record a 1 for the bit.
- Repeat steps 2 and 4 through byte 52.
- Share your basis with Alice for each byte to compare. Circle those bytes that match. (If basis does not match, disregard that byte.)
- Record the first 20 circled bits in order from the matched basis to generate the key (key bit)
- Complete Table 2 to decrypt Alice’s message:
- Enter the received bits in order from Alice (received bits).
- Copy the key bits into the appropriate line (key bit).
- Combine the received bit and the key bit for each column using the “calculation rules” for binary addition creating the decrypted bit (data bit).
- Translate each group of five data bits into the appropriate letter.
How QKD works if there is an eavesdropper?
Current communication systems rely on RSA keys to protect from eavesdropping, but the security of information is limited by the computational power of the eavesdropper. QKD, on the other hand, offers a powerful tool to encode information in superposition states of 0 and 1 bits, such that any eavesdropping can be detected. Such actions will change the superimposed bits (qubits) to classical 0 or 1 bits. The no-cloning law of quantum mechanics states that quantum information of this kind cannot be copied or amplified, and the inability to copy quantum information is not a limitation of any machine, but the fundamental limit imposed by quantum mechanics.

An example of the communication of a quantum state by Alice, Bob, and Eve.
Suppose Alice wants to send the message ‘HIDE.’ If she sends it directly to Bob by using classical information (0 or 1 bits), there is a chance that Eve can secretly copy and receive the message. Instead, Alice decides to share a secret code, a key, with Bob using the QKD protocol. She uses an apparatus, which can generate photons with four possible polarization directions. The polarization of the direction of field oscillation can be along the horizontal (0°) or vertical (90°) axis, which constitutes a so-called “+” basis. The polarization can also be in the diagonal (45°), or anti-diagonal (-45°) directions, forming the “x” basis. Note that these polarization states are linear polarization and can simply be achieved by rotating the angle of the laser, which puts out linearly polarized photons.
Currently, the laser does not produce polarized single photons and instead is an unpolarized laser pointer. Even that is sufficient to demonstrate the principles of QKD. The light is first polarized using a polarizing beam splitter, and then its polarization angle is controlled using a polarizing plate. The single-photon detection behavior is simulated by the detectors, and in a real QKD experiment, single-photon detectors are used. We assign bit numbers 0 and 1 to the polarization in both bases. The generated bits can be 0 or/and 1 on + or x basis. For example, when the polarization angle is 0° or 90°, the corresponding bit is 0 or 1, respectively, in the + basis. Similarly, setting the angle of the polarizer to -45° or +45° defines the 0 or 1 bits in the x basis.
Alice randomly chooses the types of polarization of photons and sends it to Bob. Bob then randomly decides the basis for measuring the polarization of photons. Bob’s measurement device consists of a waveplate, a polarizing beam splitter, and a pair of detectors. Depending on the polarization of the photon prepared by Alice and the polarization basis chosen by Bob, either of Bob’s detectors will click. Since detectors simulate single-photon detection events, one and only one detector will click for any incoming pulse of light.
Alice and Bob record the basis they used, and then Bob communicates to Alice the basis he used for different detection events via a public channel. Bob does not share the information about which detector clicked, but only the basis (angle of the polarizer before the polarizing beam splitter). Alice compares Bob’s basis with her original basis to identify which events share the same basis. She then tells Bob to keep the result of measurement for those subsets of events and discard the rest. In this way, the selected detected events are linked with the same information sent by Alice.
Up until this point, Alice and Bob have shared a random key (the selected bits), but it is not sure if the key is a secure one. This is the point where Alice and Bob can confirm the presence of Eve. If there is no eavesdropper, the string of bits should be identical because all the photons have been successfully transmitted. However, if Eve exists, there is a possibility that Eve alters the photons’ polarization state by detecting and reproducing the state by chance.
Alice and Bob then share a fraction of the key via the public channel to estimate the error on the key. A detected error of more than 75% confirms the presence of an eavesdropper. When the protocol is completed, Alice and Bob will be able to use the key to encrypt, transmit and decrypt the message or the word, ‘HIDE’ using the binary transformation of letters and adding the bits of the word to that of the key to protect the message. As only Alice and Bob have access to the key, only they can decrypt the message.
For example, if Alice wants to send the bit 0 in + basis to Bob, she sets her polarizer angle to 0°. Eve has a 50% chance of choosing the correct basis as Alice and a 50% chance of preparing the same state as Alice before sending it to Bob. The odds of Eve obtaining the same information as Bob is 50% × 50% = 25%. An example of this process is shown in Figure 3.
As an example, consider Alice needs to encrypt the word ‘HIDE’ into 0s and 1s by using the binary representation table shown in Figure 4. After Alice and Bob agree on a secure key, they use it to encrypt and to decrypt a message.
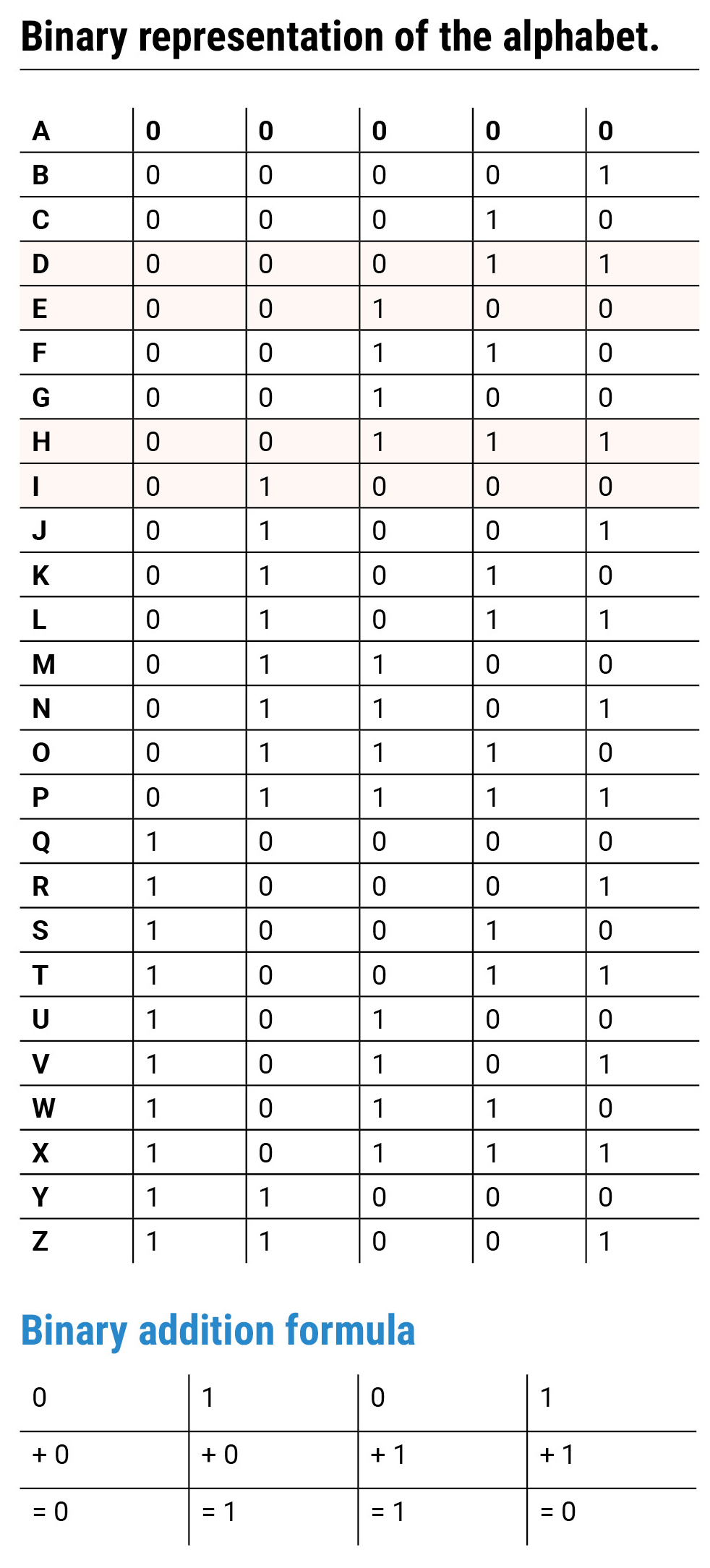
Binary representation of the alphabet.
Assessment
After completion of this experiment, high school students will be able to:
- Differentiate quantum bits (superposition of 0 and 1) from classical bits (0 or 1).
- Identify the roles of Alice, Bob, and Eve.
- Engage in the experimental process of QKD.
- Be able to perform simple binary operation and encoding of the word “hide.”
- Encrypt, transfer, and decrypt the word “hide.”
As a formative assessment, distribute exit tickets to each student to evaluate how well students understood the concept of QKD. Let them think about naming one important thing they learned in this class, something that has left them puzzled, and sharing how this new technology can be applied to our daily lives by referring to the examples of certain famous companies working in this field.
Conclusion
This experimental activity uses active, collaborative, inquiry-based learning techniques to engage students in hands-on learning, evaluating and discussing the fundamental steps of quantum key distribution, and understanding the technical details behind this novel and rapidly developing technology. We hope that the inquiry-based nature of the lesson creates interest for high school students toward learning quantum technologies as well as careers in quantum-related professions. ■
Online Connections
Making sense of the hiding states of photons: https://www.youtube.com/watch?v=z1GCnycbMeA
Interactive simulation of QuViS Quantum Mechanics Visualization Project: https://www.st-andrews.ac.uk/physics/quvis/simulations_html5/sims/BB84_photons/BB84_photons.html
Instructive videos by PBS learning media:
https://www.pbs.org/wgbh/nova/video/quantum-confidential
Zeynep Gonca Akdemir (zakdemir@purdue.edu) is a PhD student in Science Education, Muhsin Menekse is an Assistant Professor of Engineering and Science Education, Mahdi Hosseini is an Assistant Professor of Electrical & Computer Engineering, Arindam Nandi is a PhD student in Electrical & Computer Engineering, and Keiichiro Furuya is a PhD student in Physics, all at Purdue University, West Lafayette, IN.
Computer Science Labs Physics High School


