Focus on Physics
Exponential Growth and Doubling Time
The Science Teacher—July/August 2020 (Volume 87, Issue 9)
By Paul G. Hewitt
How often do we hear the adage, “Growth is good?” An economy that grows is good. Growth in income is certainly good. In general, growth is seen as a good thing. A global pandemic challenges this notion. Let’s be careful of what we wish for—especially if growth is exponential.
Exponential growth
When a quantity such as money in the bank, population, or the consumption rate of a resource grows steadily, at a fixed percentage per year, we say the growth is exponential. For example, investment accounts may grow at 2% per year; the population of a region may grow at 3% per year, and electric power generating capacity in the United States may grow at about 7% per year (as occurred during the first three-quarters of the twentieth century).
Much of the growth in the world around us is exponential. The curve in Figure 1 depicts exponential growth for any of the above examples. Notice that each of the successive equal time intervals on the horizontal scale corresponds to a doubling of the quantity on the vertical scale. This doubling of quantity becomes startling when you find the car you financed to purchase costs nearly twice as much as if you paid cash. When the growth of a quantity is exponential, the amount doubles in a certain interval of time. We speak of doubling time.
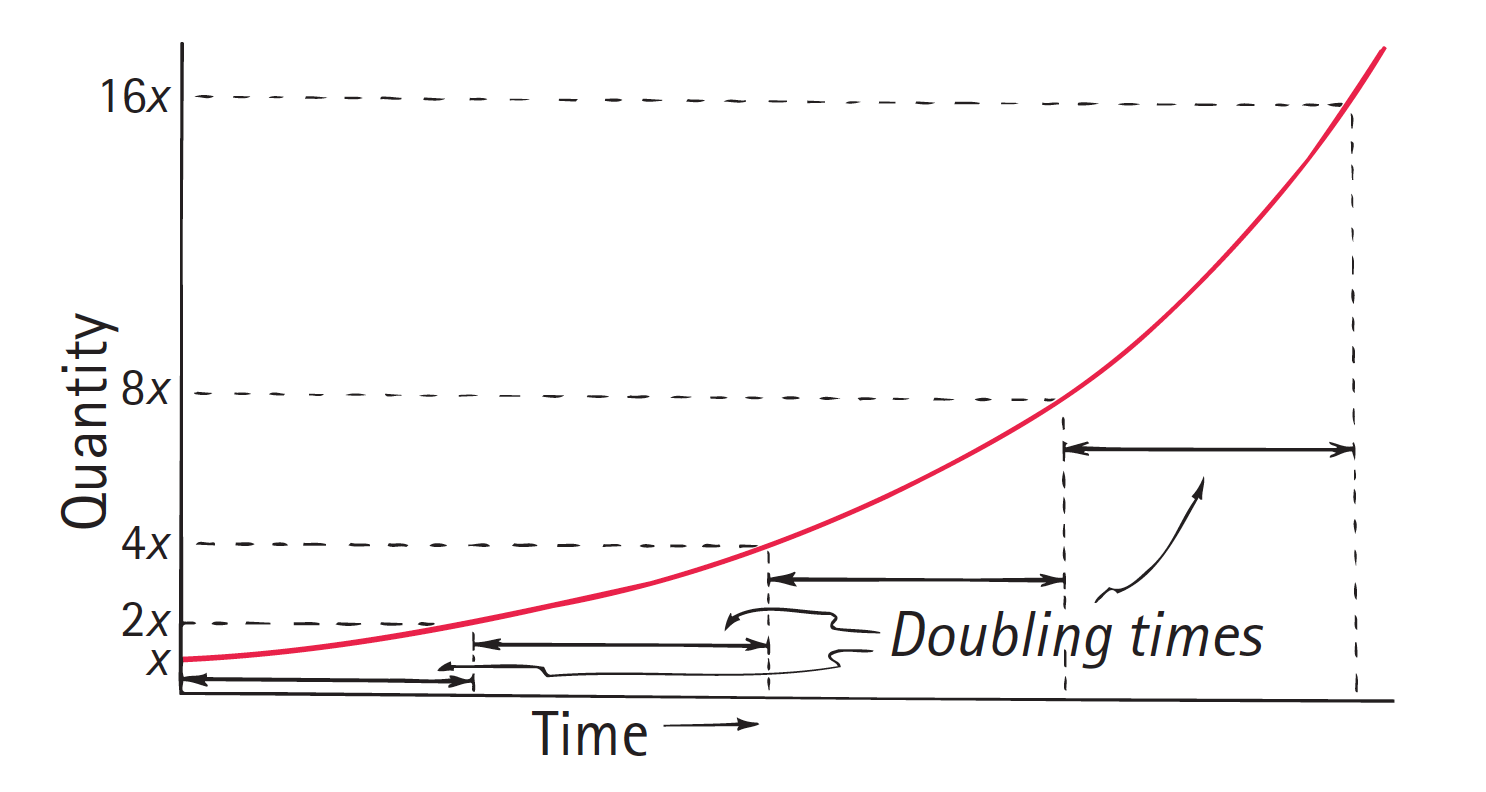
An exponential curve.
Doubling time
The importance of the exponential curve of Figure 1 is that the time required for the growing quantity to double in size, a 100% increase, is a constant. For example, if the population of a growing city takes 10 years to double from 100,000 to 200,000 inhabitants and its growth remains exponential, then in the next 10 years the population will double to 400,000 and 10 years after that to 800,000 and so on.
There is an important relationship between the percent growth rate and its doubling time known as “the rule of 70”: to estimate the doubling time for a steadily growing quantity, simply divide the number 70 by the percentage growth rate. For example, if Bozeman, Montana, maintains an annual growth rate of 4%, its population will double every 17.5 years (70/4 = 17.5 years). Space for any growing population must be planned. A city planning commission that accepts what seems like a modest 3.5% annual growth rate may not realize that this means that doubling will occur in 20 years; that’s a need for double capacity for such things as water supply, sewage-treatment plants, and other municipal services every 20 years.
If you wait until your money in the bank doubles due to an interest rate of 2% per year, get ready for a 35-year wait.
Exponentially growing bacteria
Steady growth in a finite environment gets interesting. Consider bacterial growth by cell division, in which one bacterium becomes two, the two divide to become four, the four divide to become eight, and so on. Suppose the division time for a certain strain of bacteria is 1 minute. In this steady growth the number of bacteria grows exponentially with a doubling time of 1 minute. Further, suppose that one bacterium is put in a bottle at 11:00 a.m. along with adequate food, and that growth continues steadily until the bottle becomes full of bacteria at noon.
Consider this question seriously: When was the bottle half full? What’s your answer? Can you see the bottle was half full at 11:59 a.m., 1 minute before noon? The bacteria indeed double in number every minute! It’s startling to note that at 2 minutes before noon the bottle was only 1/4 full. Table 1 shows the last few minutes before noon in the bottle.
Table 1. The Last Minutes in the Bottle
|
Time |
Part Full (%) |
Part Empty |
|
11:54 a.m. |
1/64 (1.5%) |
63/64 |
|
11:55 a.m. |
1/32 (3%) |
31/32 |
|
11:56 a.m. |
1/16 (6%) |
15/16 |
|
11:57 a.m. |
1/8 (12%) |
7/8 |
|
11:58 a.m. |
1/4 (25%) |
3/4 |
|
11:59 a.m. |
1/2 (50%) |
1/2 |
|
Noon |
full (100%) |
none |
Here’s a more important question: If you were an average bacterium in the bottle, at what time would you first realize that you were running out of space? For example, would you sense a serious problem at 11:55 a.m., when the bottle was only 3% filled (1/32) with 97% of open space (just yearning for development)? The point here is that there isn’t always much time between the moment that the effects of exponential growth become noticeable and the time when they become overwhelming.
Good news! More space has been found!
Suppose that at 11:58 a.m. some farsighted bacteria see that they are running out of space and launch a full-scale search for new bottles. Luckily, at 11:59 a.m. they discover three new empty bottles, three times as much space as they had ever known (Figure 2). Four bottles quadruples the total resource space. If they are able to migrate to their new habitats, will their problem be solved?
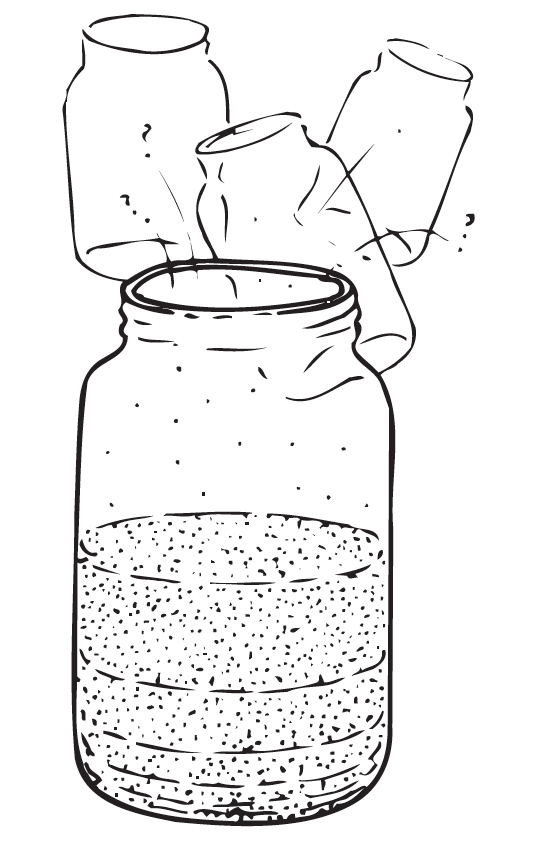
Hooray for the discovery of three times as much space!
If their growth continues at an unchanging rate, at what time would the three new bottles fill to capacity? Can you see it would be 12:02 p.m.! Just two minutes later!
Table 2. Effects of the Discovery of Three New Bottles
|
Time |
Effect |
|
11:58 a.m. |
Bottle 1 is 1/4 full |
|
11:59 a.m. |
Bottle 1 is 1/2 full |
|
Noon |
Bottle 1 is full |
|
12:01 p.m. |
Bottles 1 and 2 are both full |
|
12:02 p.m. |
Bottles 1, 2, 3, and 4 are all full |
Table 2 shows the effects of migration to the three new bottles. Only two doubling times fills all bottles. At noon the original bottle is full. One minute later bottles 1 and 2 are filled. And two minutes later all four bottles are filled. In our example the resource is space—but it could as well be coal, oil, uranium, or any nonrenewable resource.
Water lilies and the 29th day
Picture a pond with a single lily pad. Suppose that each day the number of leaves doubles, until the pond is completely covered by leaves on the thirtieth day. First question: On what day was the pond half-covered? Second question: One-quarter covered? Third question, this one with no strict answer: On what day did people who love the pond realize there was a growth problem?
The game of chess
Doubling time is intriguingly illustrated by the story of the court mathematician in India who years ago invented the game of chess for his king. The king was so pleased with the game that he offered to repay the mathematician, whose request seemed modest enough. The mathematician requested a single grain of wheat on the first square of the chessboard, two grains on the second square, four on the third square, and so on (Figure 3), presumably for all 64 squares. At this rate there would be 263 grains of wheat on the sixty-fourth square. The king soon saw that he could not fill this “modest” request, which amounted to more wheat than had been harvested in the entire history of Planet Earth!

Doubling grains of wheat on a chessboard.
It is interesting and important to note that each square contains one more grain than all the preceding squares combined. This is true anywhere on the board. Note that when eight grains are placed on the fourth square, the eight is one more than all previous grains of wheat, the total of seven grains that were already on the board. Or the 32 grains placed on the sixth square is one more than all previous grains of wheat, a total of 31 grains that were already on the board. We see that in one doubling time we add more than all that had been added in all the preceding growth! To repeat for emphasis: In one doubling time more growth occurs than in all preceding growth combined!
Table 3. Filling the Squares on the Chessboard
|
Square Number |
Grains on Square |
Total Grains Thus Far |
|
1 |
1 |
1 |
|
2 |
2 |
3 |
|
3 |
4 |
7 |
|
4 |
8 |
15 |
|
5 |
16 |
31 |
|
6 |
32 |
63 |
|
7 |
64 |
127 |
Almost universally, people (and media) use the word “exponential” to mean “fast.” If growth is speedy, they call it exponential. But exponential growth isn’t always fast, as evidenced by money growing exponentially in your savings account with annual interest 0.5% that takes 140 years to double.
The essential characteristic of exponential change is not that it is fast but that it is relentless. We’re familiar with cases of COVID-19 that grow exponentially and where small numbers of cases grow to be overwhelming—for a while.
Where the doubling time of virus cases in some cities can be three or four days, continued exponential growth would multiply the cases more than 250-fold in one month! The smaller the doubling time, the sooner other factors come into play to end the exponential phase. What feeds the growth eventually subsides, as with the 1918 flu epidemic.
Fortunately, unrestrained growth does not usually continue indefinitely. When personal growth is unrestrained, we have obesity—or worse, cancer.
Acknowledgment
I dedicate this lesson to physics professor Al Bartlett of the University of Colorado (Figure 4), who admonished us with this statement:
The greatest shortcoming of the human race is our inability to understand the exponential function.

Albert Bartlett.
On the Web
See complementary student tutorial screencast 147 on www.HewittDrewIt.com, and on www.ConceptualAcademy.com.
Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, 12th edition; Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, new 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.


