“Oh my gosh, I think it’s going to work!” a child exclaimed as her prototype crossed a river in the middle of the Amazon Rainforest. Because students have often been conditioned as passive learners and receivers of knowledge, it can be difficult for them to persevere in solving authentic problems. Nevertheless, we must persist in preparing students as problem solvers and critical thinkers. In an urban inner-city neighborhood school in the southeast, students embarked on a unique adventure created to engage them as scientists and engineers on an interdisciplinary science, technology, engineering, and mathematics (STEM) adventure.

In this article, we share how connections between the STEM disciplines can be meaningfully constructed for elementary students. In our inquiry, third-, fourth-, and fifth-grade students modeled, designed, evaluated, and tested Lego WeDo 2.0 robots as solutions to crossing a river in the Amazon Rainforest.

Table 1 highlights what the students did as well as how it connects to the STEM disciplines. Through the rich problem statement, the STEM subjects became organically blended. Consider that when problem statements are well developed, differentiation is naturally presented, as the problem itself is one in which all students can enter while the level of sophistication in which students can address the problem is open (Bush and Cook 2018). Developing a rich and meaningful problem statement is critical to bringing the STEM subjects together so that students can use knowledge and skills from each discipline in pursuit of the solution.

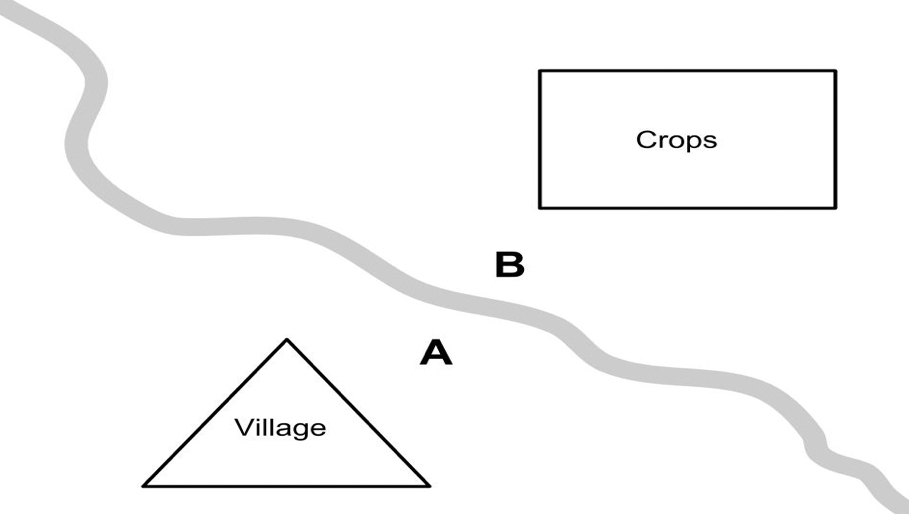
This interdisciplinary inquiry was completed over three one-hour sessions. Students were given a problem statement (Figure 1) and worked in self-selected partner teams to build and code a robotic prototype to cross a river in the Amazon Rainforest—collecting crops along the way. Prior to this inquiry, we spent time modeling how to work within partner groups. As a class, we developed norms that were reviewed prior to the inquiry and because of this, students had the opportunity to self-select their partners. Figure 2 provides a list of the norms that students created. Some grouping strategies might include grouping based on previous experiences or mathematical/scientific interest. Although a basic understanding of coding robotics would be helpful in completion of the task, students did not have any prior knowledge or experiences with this before beginning this inquiry.

We provided students with the following materials: Lego Wedo 2.0 Robots, blank white paper to draw the river, rulers, pencils, computers for coding, and string for their prototypes. To aid students in modeling the scenario, they were encouraged to draw early designs of the robotic prototype. Figure 3 depicts the picture that was given to the students, which was intentionally left undescriptive so that students could imaginatively recreate the scenario. This also increased students’ communication centered on modeling the mathematics and the science content as student groups were required to describe to their peers what they imagined the area looked like. Students shared thinking such as: the river bank would be very muddy, there is a thick jungle, and there is an abundance of wildlife near the water. Interestingly, this also built opportunities for students to develop deep rationales for the design of their robots, because they needed to be able to communicate their reasoning to their partners to collaborate effectively. One of the items that students discussed in their groups was the placement of their robotic designs within their modeled rainforest region. When explaining and supporting their thinking, students were encouraged to incorporate what they knew about weathering and erosion to select the best area to build their prototypes so that the river would not destroy their creations (in the way the bridges were destroyed).

Armed with their problem statement and task directions, the teacher led students in a brainstorming session to grasp the scope of the task. During this time, we prompted students to visualize the scenario by closing their eyes and imagining what the Amazon Rainforest and river looked like. Students recorded questions they had about the task, such as: How long is the river? What is in the river? and How fast does the river flow? We focused on students’ understanding of the task and did not answer any questions that might push the students on a singular solution path. Next, students worked with their partner to draw out on paper their initial solutions (see Figure 4 for an example of a student drawing). We circled the room to listen and engage students in conversations about their early ideas. We also encouraged students to use the robotic kits to aid in their early designs. Doing so contributed to student designs being more realistic as well as plausible to match the pieces of the Legos. Working with the robotics kits also served as an opportunity to acquaint students with the Legos as tools of the inquiry and not simply as toys. Once student designs were drawn on paper, we shifted to the mathematics.

Students worked to scale the width of the river to model their robotic designs across several sheets of paper. They were given the scale of 1 inch on the provided picture = 12 inches on the scaled drawing. This was intentional so that students had to model across several sheets of paper as the length of paper is typically 11 inches, instead of simply counting pieces of paper and spreading them out. Students employed multiple ways of solving. For example, some students noted after measuring that the width of the river was 3 inches and then subsequently multiplied 3 inches × 12 inches, determining a total width of 36 inches. They then laid out multiple sheets of paper and measured 36 inches, marking the beginning and end of the river width. For most students, this was the first time they had worked to scale distances. We found this to be an authentic opportunity to highlight measurement ideas. Students used rulers to measure the distance across multiple sheets of paper. They measured 12 inches iteratively three times, so students were learning to use the structure of repeated addition to make sense of the multiplication. This is a critical concept spanning mathematics and science and directly related to the problem under investigation because students would soon be reasoning with scale when considering the rotations of the robot wheels in their coding. Students finished the day by planning out their next steps.

We began with a whole-class discussion on the weathering and erosion that the river had caused upon the previous bridges built by villagers. Students determined that bridges eroded because the water flowed extremely fast through the support beams (the student who drew a drawbridge elected to change their design shortly after this discussion, as they noted it would not last a long time with the river rushing around it). Students watched videos of water rushing against bridges to explore the long-term effects. Students then used this idea to adjust their previous designs and began to build their robotic solutions to the inquiry. Students worked diligently with their partners to build their solutions. As we circulated the room and listened, we strategically highlighted specific student conversations to drive the thinking of the entire classroom. For example, we highlighted one group’s conversation about the placement of a robotic wheel. The partner group noted that they did not want it to be too close to the water, as it would rust or deteriorate over time just like the bridges. To successfully complete the task, student pairs needed to move a carrying box from point A to point B on their modeled river. Throughout their building time, they honed their thinking of Cause and Effect, a crosscutting concept. At the end of this session, students were asked to share how their designs would affect the natural habitat of the area as well as the river itself. One partner group displayed the effect by placing one hand in front of them and moving their other hand around it in a circular motion to demonstrate the rotations the robotic wheel would take pulling in the string around the fixed hand. The teacher pushed this thinking by prompting students to also consider the placement of their robotic wheels. Partner groups began thinking about how it would influence the river bank if it were too close to the water as well as how the wildlife would be influenced if the cart was pulled across the riverbed.

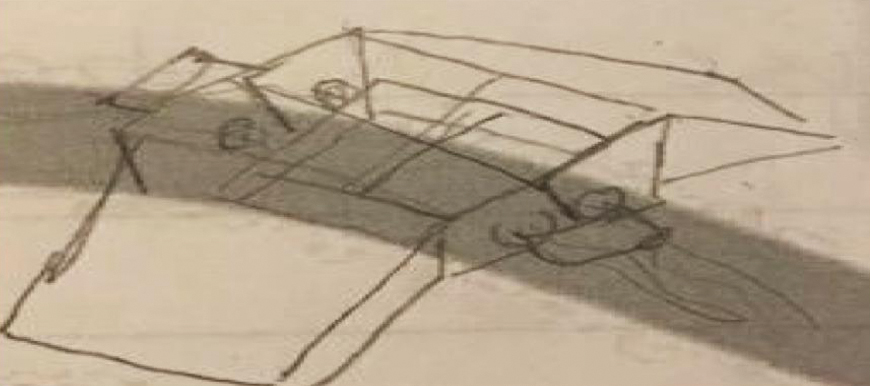
The teacher noted several student conversations that were filled with both excitement and wonder. Students said things such as, “I can’t believe we are getting to do this for science today,” “We are really going to figure this thing out next time,” “I cannot wait to tell my friends about this tomorrow,” and “My parents will never believe I am doing this in school.” Students completed session 2 with a robotic prototype. Figure 5 showcases a sample student prototype.

On the final day, students began by physically demonstrating the movements they wanted their robots to complete. This was the point at which students began the coding process and applied much of what they had learned about proportional reasoning and scaling. The previous sessions established an authentic context and understanding of scaling, and students used this to think through how to program their robots. During this time, we revisited Mathematical Practice 8 to aid students in making use of the structure and patterns of the wheel rotations. Because the students would need to plan for the amount of rotations it would take to get across the entire width of the river, we prompted students to examine the pattern of the robotic movements and intentionally pay attention to how far one rotation would travel. Students could use the distance of one rotation to predict how far multiple rotations would pull the cart across the river. Measurement and proportional reasoning was essential so that students could make mathematical predictions for their robot’s movements, which was also an opportunity to focus on the SEP of Using Mathematics and Computational Thinking. The teacher asked, if one rotation makes their robot move 2 inches, how many rotations would it take to make the robot move 36 inches? How do we know? Students then set out to determine how many rotations it would take to travel the total distance of the river. Due to students needing to code the robots to pull the carrying box across the modeled river, they focused on the rotational movements of the wheel pulling and collecting the string. Some students ran trial and error tests to determine it would take 18 rotations to reach the other end of the river.

Meanwhile, other students thought about the pattern of the rotations and noted that it would move the same distance every single rotation. These students used this information to think multiplicatively and determine the robot would need 18 rotations to reach the other side. Note that this same learning goal can be reached by having students create a wheel to collect string and predict how many spins it would take to pull the box across the river. This would, however, not incorporate any coding but does provide an access point for schools that do not have technology. Figure 6 showcases the final product created by one partner team. This example displays a robotic wheel that turns in a circular rotation. As it turns, it collects the string around the wheel. As the robotic wheels pull in string it pulls a cart from one side of the river to the other. This partner group went on to explain that their design addresses the weathering and erosion concern by placing the robotic wheel farther back from the river bank to not disturb the loose or muddy soil, as this would result in part of the bank being washed away. They also determined that their cart would float across the river, so as to not disrupt the underwater habitats. While this design is presented, there are a multitude of designs that could be incorporated to complete the task at hand. Throughout this session, students began to shift their future aspirations from professional athletes to future scientists and engineers. Each student smiled and exchanged high-fives as their robotic prototypes demonstrated high-level coding by successfully moving across their modeled river (see Figure 6, p. 34).

Students were assessed based on their abilities to explain how their prototypes served as solutions to the problem statement. Students explained their final designs and demonstrated how it would collect the crops and then cross the river. We wanted the assessment to be as student-driven as the task, so we incorporated a rubric. Through their explanations, students had the opportunity to demonstrate their understanding of CCSSM 5.NF.B.5, interpret multiplication as scaling, because they were demonstrating the robotic movements upon their scaled drawings. Students were also prompted to explain how they developed their scaled drawings. Students stated ideas such as: measuring one ruler length (12 inches) and marking the end three times to equal 36 inches; and 3 inches × 12 inches was 36 inches and thus they measured 36 inches across multiple sheets of paper. Students should have the opportunity to continually connect their learning back to the context, particularly in identifying the disciplinary content knowledge that aided in their solution (Bush and Cook 2018). One partner group demonstrated their movements and explained that they programmed their robotic wheel to do one rotation. After the rotation, they measured the distance it traveled from the river bank. They noted it traveled 3 inches. They then measured 3 inches iteratively, marking each segment, until they reached the other side. The partner group then counted the segments and knew it would take 12 rotations to reach the other side. We suggest prompting students with questions such as: “How did your knowledge of scientific ideas help you to achieve your solution,” “What mathematical skills did you use to solve this problem,” and “In what ways did engineering help you to reach your solutions?” One partner group exclaimed, “The science really helped me think about the environment and how my design might affect the animals in and out of the river. When we did the engineering sections, it was all about the building of our designs. We really had to think hard to get everything perfect and do what we want. The math helped us to make predictions that our robot would do.”

As teachers, we have the daunting task of preparing our students for jobs that do not yet exist. We must cultivate a sense of wonder and excitement as students learn about their world. As we move forward with teaching and learning through the lens of the NGSS, it will become increasingly important to equip students with the ability to see the interconnectedness of the STEM disciplines so that they can persevere in solving authentic and real-world problems. The Amazon Rainforest River Task showcases an interdisciplinary integration in which each of the STEM disciplines were incorporated meaningfully. Furthermore, this inquiry highlights an authentic learning opportunity for students to collaborate as learners and problem solvers. Students were critically engaged in their learning as evident in their designs and through the rich conversations centered on the inquiry. Students routinely arrived to work on their task with new ideas to incorporate based on their reflections from the previous session. Students noted the importance of each discipline in unlocking new viewpoints or perspectives as they worked toward a solution. We hope this highlighted experience ignites in you a passion to attempt a challenge such as this one—transforming student learning!