feature
Beam Analysis in Statics Courses Using ReshmoBeam
Journal of College Science Teaching—May/June 2021 (Volume 50, Issue 5)
By Joel Hernandez, Rafael Niyazov, and Kibrewossen Tesfagiorgis
This article describes the use and advantages of the MATLAB-based program ReshmoBeam, developed to perform beam analysis, as it is done in statics courses of engineering curricula. An important goal of the article is to facilitate the dissemination of the program among faculty teaching these courses. The program is offered free to interested faculty for potential application in their courses. The program is not intended to compete with existing software for this purpose. Existing programs can be comprehensive; however, the user must pay to use all or some of their features. ReshmoBeam covers a limited, but important range of situations in beam analysis. The program determines the reactions at the beam supports, the shear and bending moment values at points specified by the user if desired, and the maximum values of shear and bending moment. The program also generates the loading, shear, and bending moment diagrams for the beam situation under analysis. Students can quickly verify the correctness of their manual calculations and also explore a diverse range of loading conditions. Furthermore, its use could facilitate a deeper understanding of the material taught in the course.
The determination of the reactions from beam supports, the calculation of shear forces and bending moments, and the generation of shear and bending moment diagrams, are important topics covered in engineering statics courses (Beer et al., 2015). In addition, the determination of the maximum value of shear and bending moment, and the location where these maxima occur along the beam, are essential for the design of beams that are able to safely resist applied loads (Limbrunner et al., 2015). Students are required to perform manual calculations of these quantities and draw the shear and bending moment diagrams. The calculations can be laborious, but necessary for the understanding of these topics. We developed ReshmoBeam, a free MATLAB program for students that performs these calculations and generates the needed diagrams. However, it is not used to replace the important and required manual calculations. The scope of the ReshmoBeam program is as follows:
Types of beams and supports:
- Simple and overhanging beams supported by a pin and a roller
- Cantilever beams
Types of loads:
- Point loads
- Distributed loads (uniform, triangular, and trapezoidal)
- Concentrated moment loads
Calculations and diagrams offered:
- Reactions from the beam supports
- Shear and bending moment at points requested by the user
- Maximum value of shear and bending moment
- Loading, shear, and bending moment diagrams
This article includes a theoretical background section, where a representative example is solved manually to illustrate the principles and methods involved. The source code of ReshmoBeam is not included due to space constraints. Readers are encouraged to request this software from the corresponding author.
Theoretical background
This section uses the loaded beam shown in Figure 1a to briefly describe the theoretical principles and methodology used to perform beam analysis.
Determination of the reactions RA and RC at the supports A and C:
The magnitude of the equivalent resultant force of the distributed load is determined as W = w L = 70 kN. The point of application of this resultant force is 5 m from the left end of the beam (see Figure 1b). RA is determined from the moment equilibrium equation about point C:
ΣMC = –RAL +WL3 + PL2 = 0
From this expression, the value of RA is obtained as RA = 45 kN. Rc is similarly found by taking moments about point A, resulting in the value Rc = 75 kN.
Determination of the shear V and bending moment M along the beam:
Shear is calculated as the sum of the external forces acting on a section of the beam to the left of a cutting plane (see 2e). Bending moment is calculated from the moment equilibrium equation on this section of the beam, with the center of moments taken at the intersection of the plane with the horizontal axis.
From A to B (plane at 1): The forces RA are and the distributed load up to point 1, as seen in Figure 2a.
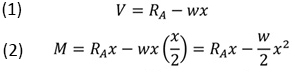
From B to C (plane at 2): The forces are, RA, P, and the distributed load up to point 2, as seen in Figure 2b.
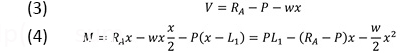
The shear and bending moment diagrams are shown in Figure 3. The maximum shear for this example is VMAX = 75 kN. This is found by evaluating equation (3) at x = 10 m, and taking the absolute value of the result. The maximum bending moment occurs at the point of zero shear. This point (x = 6.43 m) is found by setting V = 0 in equation (1) and solving for x. The maximum bending moment (MMAX = 144.64 kN.m) is subsequently determined by evaluating equation (2) for x = 6.43 m.
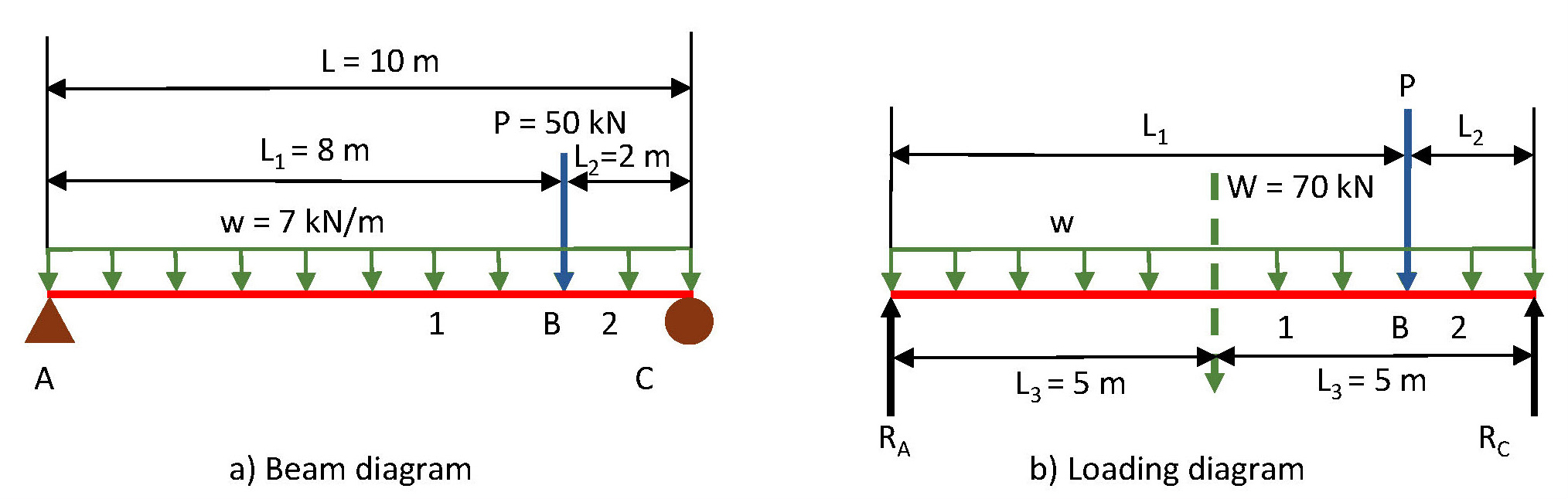
Beam and loading diagrams used to calculate the reactions RA and RC.
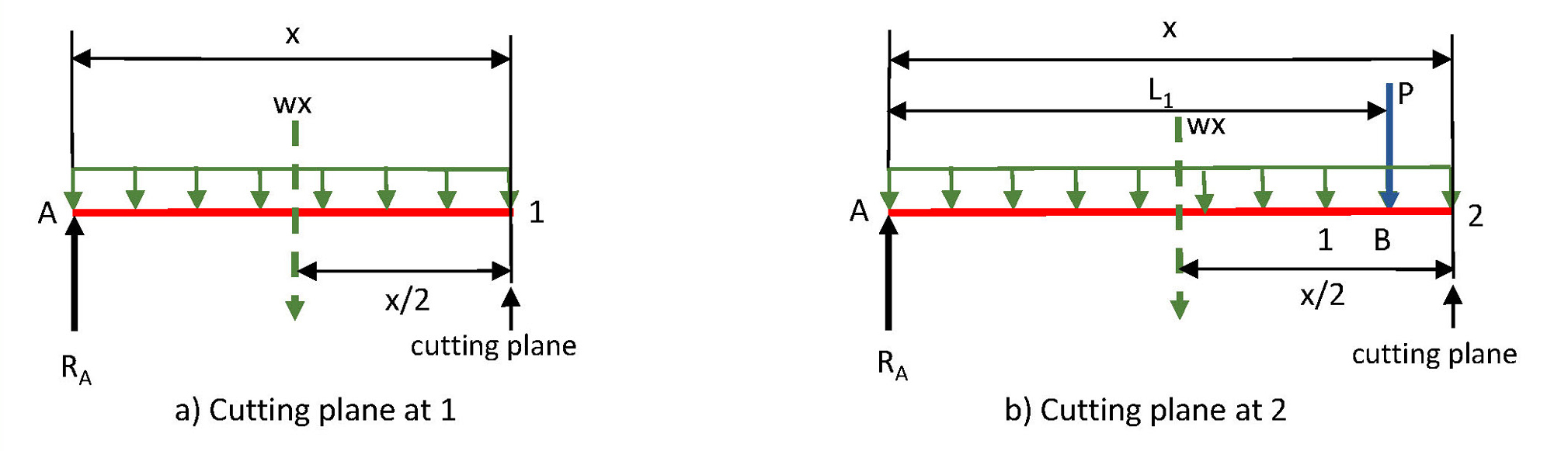
Diagrams used in the calculations of the shear and bending moment.
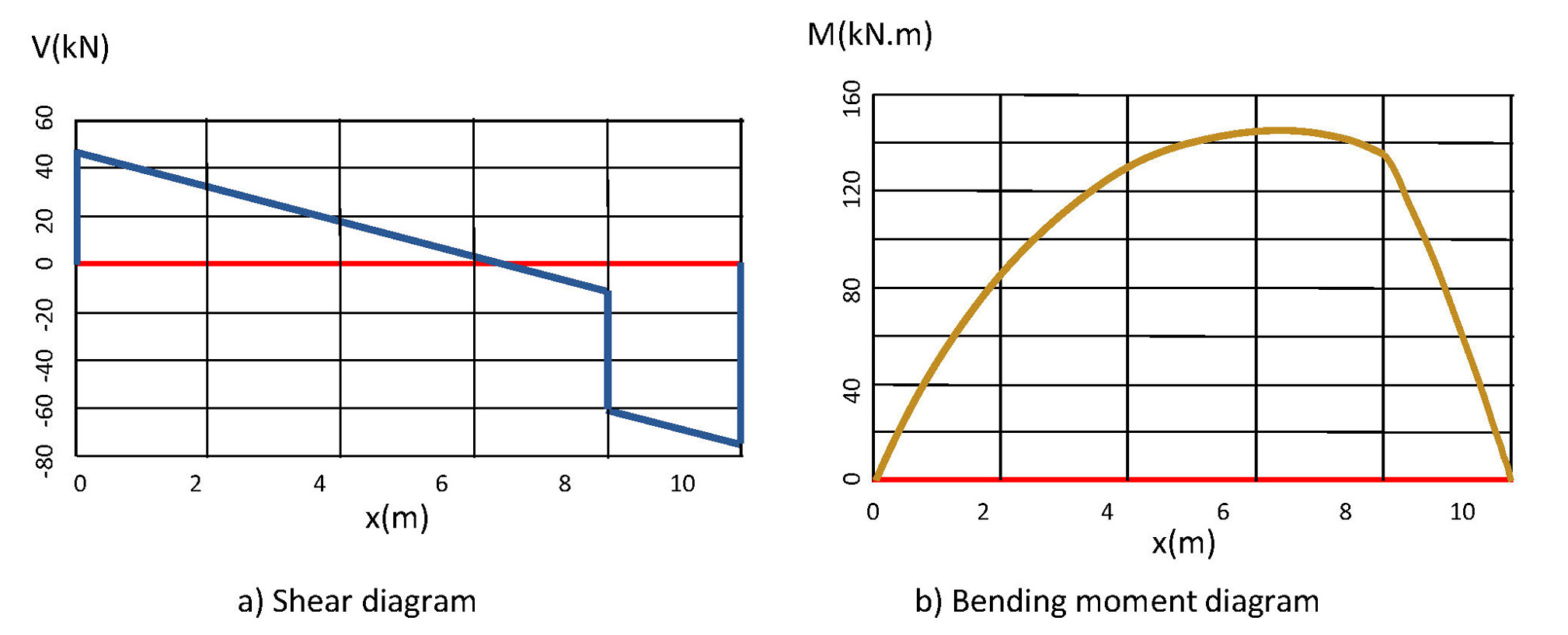
Shear and bending moment diagrams generated using the manual calculations results.
Software details
Execution of the program: The name ReshmoBeam is a reference to Reactions, shear, moments, and Beam. The program runs by typing ReshmoBeam at the command window of MATLAB.
Data entry: This is done via the keyboard.
Display of results: The command window shows numerical results. The graphics window displays the loading, shear, and bending diagrams, as well as the magnitudes of the reactions.
Sample execution: The execution sequence for the example in this paper is described below.
Informational screens
The program provides two informational screens in the command window and one in the graphics window. The command window specifies the calculations and diagrams offered, the types of beams and loads accepted, and the sign conventions for forces, moments, positions, and angles. The graphics window illustrates how loads are represented in the diagrams. When the graphics window appears, the user should drag it to the side of the command window and resize it to occupy most of the vertical dimension of the screen.
Data input: Table 1 shows abbreviated data entry requests, and the corresponding user inputs. During execution, the user receives explanations to input the information correctly, as shown in Figure 4.
Command window text output corresponding to data entry request # 6 in Table 1.
Enter the position, magnitude, and angle for point load # 1
The position is +, measured from the LEFT end of the beam, and given in meters
The magnitude is +, and given in kN
The angle is +, measured ccw from the + horizontal axis, and given in degrees
Enter data in the format [Position, Magnitude, Angle]; for example, [8,50,90].
Don’t forget the square brackets!

Text output of the numerical results in the command window.
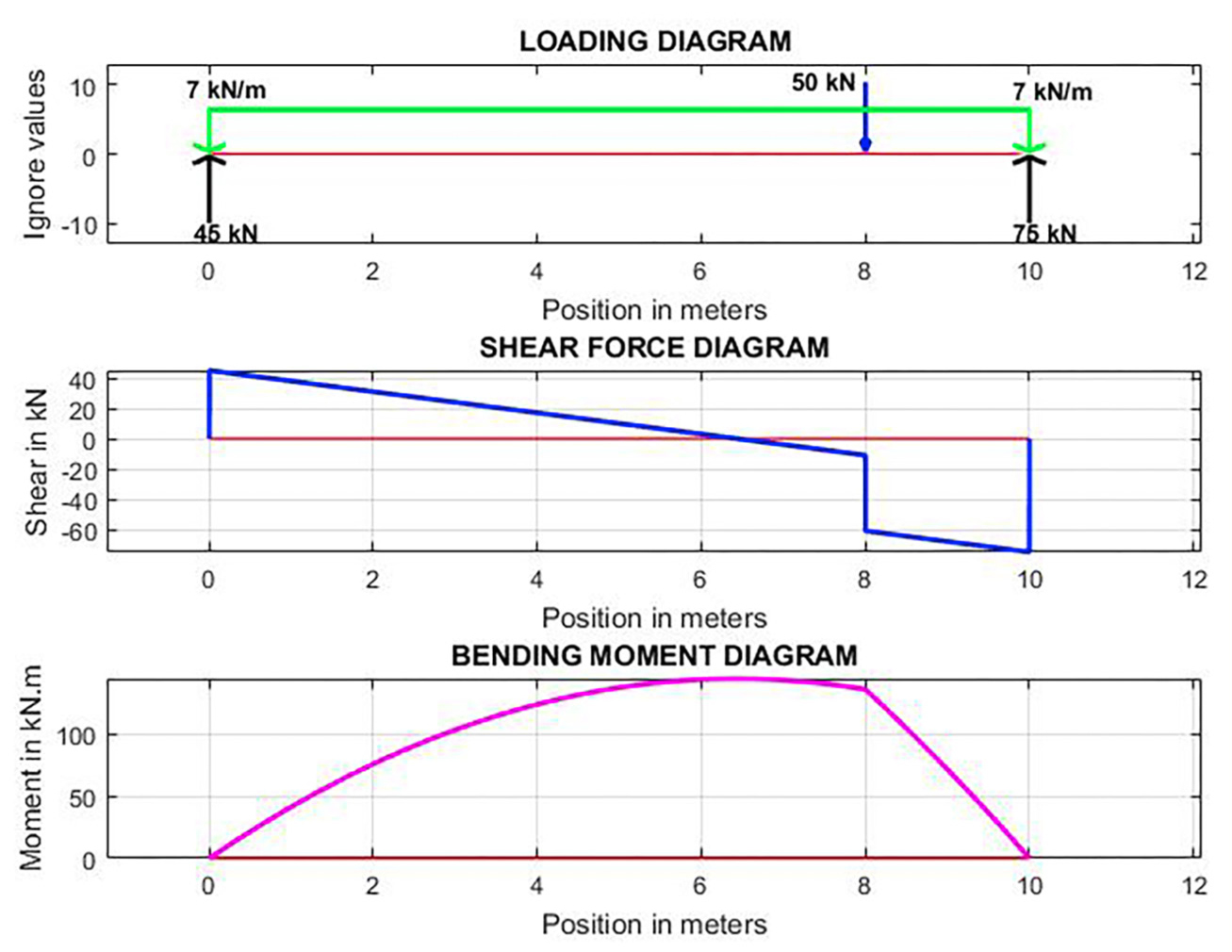
Loading, shear, and bending moment diagrams produced by ReshmoBeam.
Comparison with existing software
Table 2 compares ReshmoBeam with available software to perform beam analysis. This comparison is limited to the features offered by ReshmoBeam. Items that require payment, or that are not offered at all, are marked with the symbol x. ReshmoBeam offers all the listed features for free, including its MATLAB source code.
Beam Calculator Online from BeamGuru (2020), offers the text of the calculations step by step, free of charge. We do not offer this feature because students need to manually solve the problems by themselves to develop necessary skills.
Some programs offer features that are not needed in our engineering statics course, and for that reason, ReshmoBeam does not offer these features. For example, deflection is offered for free by Online Beam Calculator from SkyCiv Engineering (2017), by GoBeam from Polyakov (2015), by Beamanal from Tomanovich (2017), and by Beam Calculator from WebStructural (2019).
Academic impact
Table 3 shows the average grades achieved by our students in the beam analysis exam questions.
Grades were higher and students appeared to be more motivated when the program was used. The course was taught by the same instructor, once per year. Two different sets of exam questions were used: one set during even years and the other during odd years. Required homework assignments during those years were comparable to each other; they differed only in the particular load positions and values. More complex homework assignments were included for extra credit when the program was used. The program was used by the instructor in class to quickly generate shear and bending moment diagrams. Students were required to use the program to produce the shear and bending diagrams for all assignments; however, manual calculations were required to derive all formulas and numerical results.
Conclusion
ReshmoBeam is useful to students and simple to use. Students are able to easily generate shear and bending moment diagrams, verify the correctness of their manual calculations, and explore diverse and complex loading conditions. They have the freedom to modify the source code, providing an opportunity to improve their MATLAB programming skills. Faculty can use ReshmoBeam to assign more complex and interesting problems to students, which could lead to a deeper understanding of the course material. The use of the program in our engineering statics course led to improved academic performance in the topic of beam analysis. ReshmoBeam offers free features that are only available in similar programs with a paid subscription. The program can be requested at any time from the corresponding author to facilitate its dissemination among teaching faculty. ■
Joel Hernandez (jhernandez@bmcc.cuny.edu) is a professor and chair of the Science Department, Rafael Niyazov is an associate professor and deputy chair of the Science Department, and Kibrewossen Tesfagiorgis is an associate professor, all at Borough of Manhattan Community College in the City University of New York in New York City.
Computer Science Mathematics Postsecondary


