In the February issue we looked at teaching speed and velocity. Now we’re ready to tackle acceleration.

This is the biggie—perhaps one of the most difficult concepts in your course. You may find it okay to hurry through the concepts of speed and velocity because they are intuitive. But you cannot hurry through acceleration quite so quickly because it is not intuitive.

Ask for the three controls in an automobile that enable it to change its state of motion—to produce acceleration. That’s the accelerator, brake pedal, and steering wheel. Acceleration can be felt in a car or motorcycle as one gains speed, when slowing, and when changing direction (Figure 1). Acceleration is the time rate of change of velocity, which includes changes in speed, direction, or both.

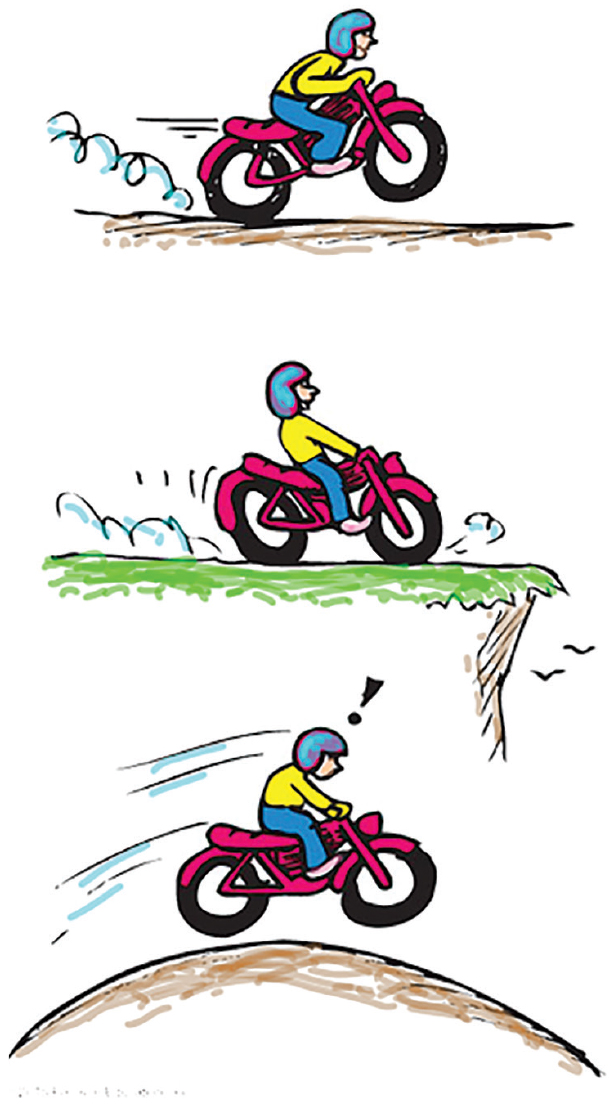
Whereas velocity is a rate of covering distance, acceleration is a rate of the rate of covering distance—or even a rate of turning. This can be twice as complicated for the learner, and, as said, it is not intuitive. An understanding of acceleration will be crucial for understanding Newton’s second law—the law that got humans to the Moon in 1969.

Ask your class to calculate the acceleration of a car that goes from rest to 100 km/h in 10 seconds, assuming uniform acceleration. Have them check their work with their neighbors as you pace your delivery. Only after they get the hang of it, introduce meters/second/second in your examples to develop a sense for the unit m/s². Be prepared for the perennial question, “Why are seconds squared in m/s²?” For inquisitive students who have difficulty with m/s² after an initial explanation, I advise they “let it go.” Move on for the time being, and more than likely it will be understood later. Wisdom is knowing when lack of initial understanding can be overlooked.

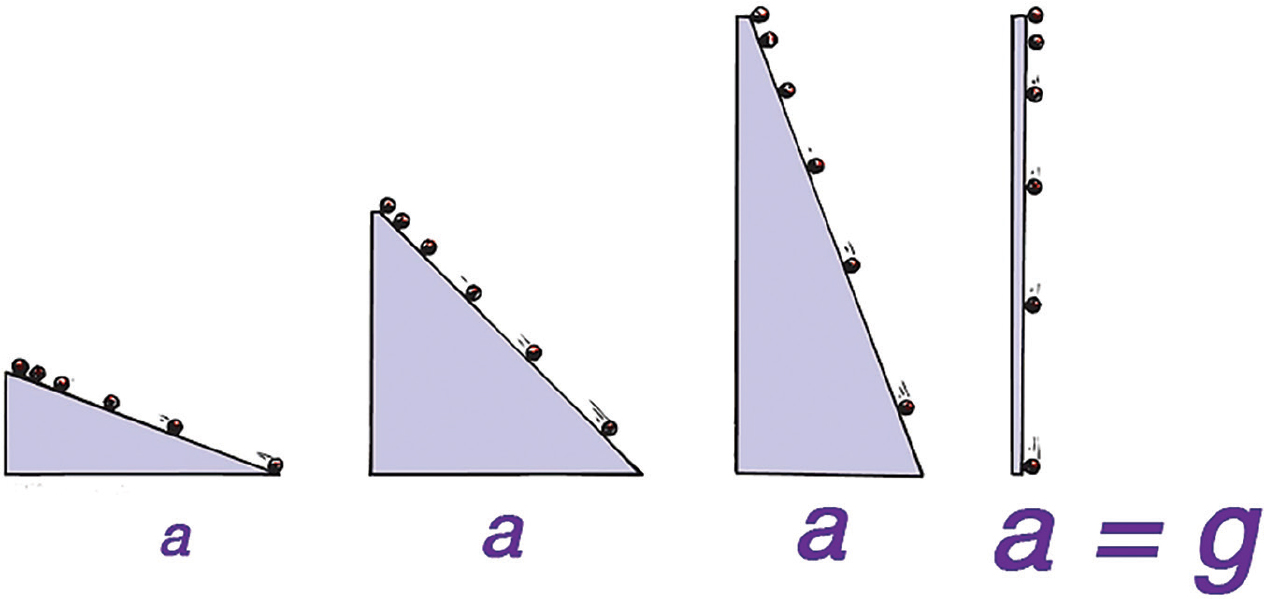
Galileo introduced the concept of acceleration when experimenting with inclined planes. He noted that a ball rolling down an inclined plane gains speed at a steady rate (a steady rate in time, not in distance). The steeper the incline, the greater the gain, and the greater the acceleration of the ball (Figure 2, where magnitudes of acceleration, a, are depicted with different size symbols). When the incline is elevated to 90°, maximum acceleration occurs—the acceleration of free fall.

Free fall means falling only under the influence of gravity—with no air resistance or when air resistance so minor that it can be discounted. Give examples of free fall such as a coin and feather dropped in a vacuum, or a boulder that drops a short distance. Falling in the presence of air resistance is not free fall. Later in your course, the physics of parachutes and skydiving will be examined. For the time being your lesson is confined to free fall. First things first.

Imagine a boulder dropped from rest from a cliff. Why from rest? Because the physics is simpler than otherwise. (Better that students understand simple physics than be confused by not-so-simple physics, at least at the outset of your course!) Further imagine that the boulder is equipped with a speedometer that can register its speed of fall (Figure 3).

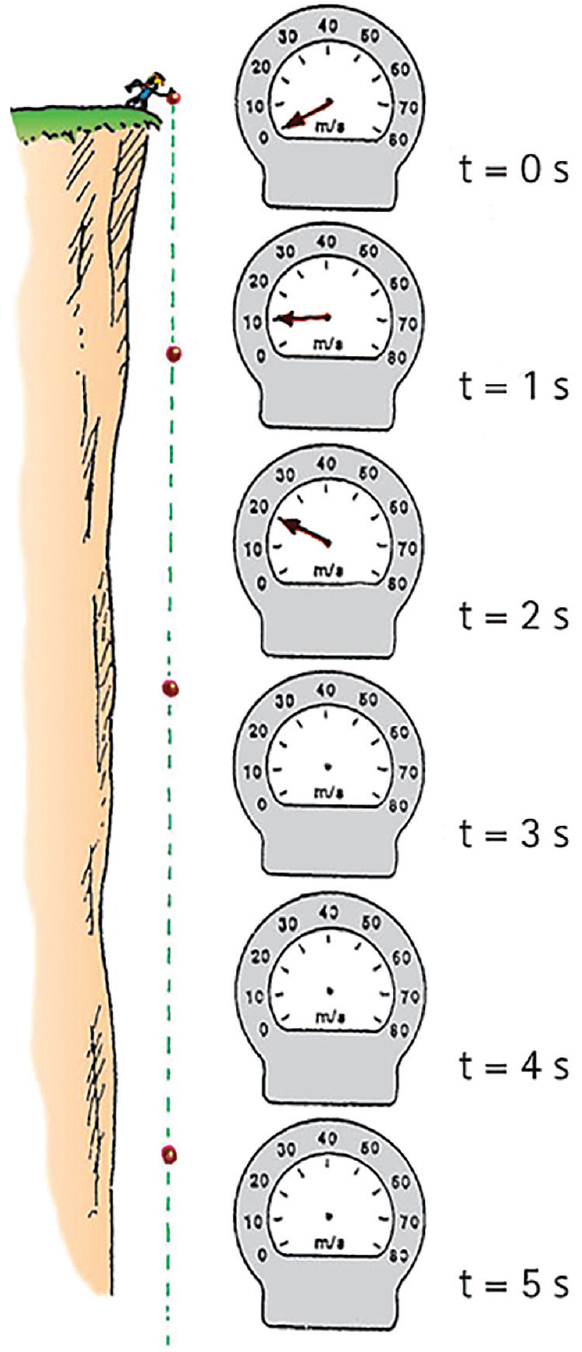
At the moment of drop, the speedometer shows its initial speed of zero.

The pattern of free fall should be evident—speed increases by the same amount each second, 10 m/s. (To help students more easily understand the sequence of falling, we can round 9.8 m/s² to 10 m/s². In lab you can use the more precise 9.8 m/s².) This acceleration of free fall is due to gravity, 10 m/s², or simply g.

So how fast is the boulder falling in each successive second? In shorthand notation v = gt, which you can relate to the speedometer readings. After questions, discussion, and examples, state that you are going to pose a different question—not asking for how fast, but for how far.

How fast something falls relates to how far something falls. Carefully derive d = 1/2gt². The derivation is not expected of your students but instead shows a reasoned statement that doesn’t just appear from nowhere. Then ask how far a freely falling object travels in 1 second. In 2 seconds? Return to the falling speedometers and inscribe the odometer readings (not shown in Figure 3). Display the distances: 5 m, 20 m, 45 m, 80 m, 125 m.

As we’ve just seen, a freely falling object falls a vertical distance of 5 m in the first second. Why not 10 m? Prompt a discussion by asking, “If you maintain a constant speed of 10 km/h for 1 hour, how far do you travel?” [10 km] Then, “If you maintain a constant speed of 10 m/s for 1 second, how far do you travel?” [10 m] In these questions, units km/h and m/s progress to distances km and m. Important point: You’ll appreciably improve your instruction if you allow sufficient “wait time” after asking a question. Not doing so is a classroom folly experienced by too many teachers.

Then continue, “Why does an object initially at rest not fall 10 meters in its first second of fall?” After a suitable “wait time,” elicit that it’s not falling at a constant velocity, and then move to the relationship between average velocity and distance traveled.

The average velocity of a uniformly accelerating object, or an object in free fall, is given by

For objects that begin fall from a rest position, the average velocity is simply half the final velocity. Whereas an object gains 10 m/s of velocity in its first second of fall from rest, its average velocity is 5 m/s. The important distinction is that while the instantaneous velocity of the falling object when it reaches one second is 10 m/s, the average velocity of fall during that one-second interval is 5 m/s. And the distance of free fall from rest in one second is 5 m.

The fascinating topic of hang time can complete your kinematics lessons. Challenge your students by promising that you’ll award an A to any student who can do a 1-second standing jump (with no equipment)! You’ll have takers; but you’ll award no As for this feat.

Hang time is the time a jumper’s feet are off the ground in a standing jump. Hang time for the best basketball players is less than a full second. The equation d = 1/2gt² predicts the vertical height of a jumper. Consider a hang time of a full second. That means 0.5 s up and 0.5 s down. The one-way distance is d = 1/2gt² = 5(0.5)² = 1.25 m (which is about 4 feet!). So the great athletes and ballet dancers jump vertically no more than 4 feet high! Of course one can clear a higher fence or bar; but one’s center of gravity cannot be raised more than 4 feet in a standing jump. In fact, very few people can jump 2 feet high!

Tell your students they can measure their jumping height and calculate their personal hang time as follows: “Stand flat-footed in front of a wall. With a marker in your upstretched hand, make a mark. Then jump upward and at the top of your jump make another mark on the wall. The distance between the two marks is your jumping height” (Figure 4). If a student jumps more than 1.25 m (4 feet), you have a world-class athlete in your class.

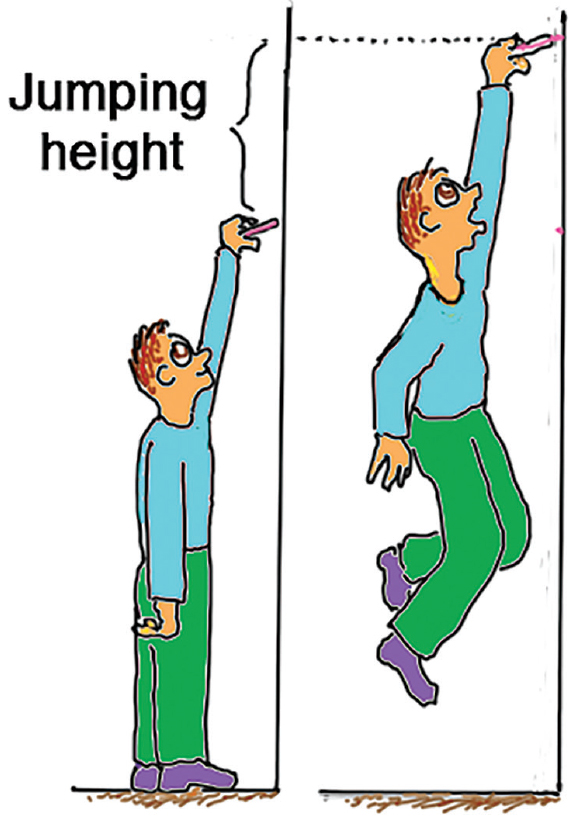
At the top of the jumper’s path, the distance to the floor is given by our now familiar d = 1/2gt², which is also the height of the jump. Solving this equation for t gives t =√2d/g. Note that this is the time for half the jump. Double t for the jumper’s hang time!

One of the great things about being a physics teacher is the relevance of your study of nature’s rules. Adding to that relevance, nothing is more inherently interesting than nature itself. As such, physics should be in the curriculum for every student.