We’re all familiar with students who can solve physics problems while having little understanding of the physics involved. To correct this, adequate classroom time should be allotted to teaching students to read and understand the equations. This applies to all high school and college physics students, as well as college engineering and science majors. 

Shorthand expressions of Nature’s laws

Nature has laws. The most basic ones are the laws of physics, nicely expressed in the shorthand of mathematical equations. For the most part, equations are the backbone of physics courses. For engineering and science students, solving algebraic or calculus-based problems is expected. Equations are essential. But their role as guides to clear thinking is too often overlooked in physics courses.

Some introductory physics courses for nonscience students minimize or avoid equations altogether. I see this as a grand mistake. I strongly recommend that, rather than bypassing equations, adequate class time should be devoted to learning to read them, to be able to articulate the meaning of their symbols, and understand how they relate to one another. 

Troubled teacher story

A story that emphasizes the value of understanding equations is that of my teaching colleague, who arrived in class one day troubled by the loss of lecture notes on Newton’s law of gravitation. Desperately, my colleague wrote on the board the equation

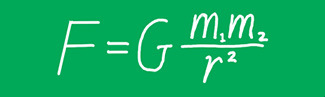
and began a teacher-student discussion about what led to the law’s discovery, what each of the symbols meant, and how their arrangement made sense. Students were involved in back-and-forth questions and discussions: “What if one of the masses were larger … or smaller … and or farther apart? What is meant by G being a conversion factor?” Suggested answers permeated the classroom, along with the story of how the first measurement of G led to the determination of Earth’s mass. All intriguing.

Not surprisingly, this entire period—focused on this one equation mixed in with a little history—was rated by students as their most highly valued class, even more than classes with demonstrations! The message here is clear: Teach students to read equations and understand the meaning of their symbols, and, when possible, share with them how the symbols and equations came to be.

Impulse and momentum

An equation that makes an appearance in nearly every introductory physics course is the impulse-momentum relationship, F∆t = ∆(mv), in which mv—mass × velocity—is momentum, ∆(mv) is a change in momentum, and F is the average force that acts over a time interval ∆t. Nice, short and sweet. This is derived by equating Newton’s second law, a = F/m, to the definition of acceleration according to Galileo, a = ∆v/∆t, which shows that the impulse-momentum relationship doesn’t pop out of thin air!

The combination F∆t is called impulse. Let’s “read” the equation. It says that the impulse supplied to a body is equal to the change in momentum of that body, as when falling onto a concrete floor versus a padded mat, colliding with an airbag versus a car windshield, or when a swung bat hits a pitched baseball. Can the equation be read the other way around? Can it say that a body’s change of momentum imparts an impulse to something else, as when a batted ball is stopped by an outfielder’s mitt? It actually says both. Like many equations of physics, the impulse-momentum equation is a relationship. It doesn’t say what is cause and what is effect. It just says that two things go together.

A classic example of the relationship between impulse and momentum is that of an out-of-control car hitting a haystack instead of a massive concrete wall (Figure 1). No knowledge of physics is needed in a driver’s decision to slam into a haystack than into a massive wall. Slamming into the haystack is intuitively the sensible choice. But why? In physics we cherish why certain things happen.

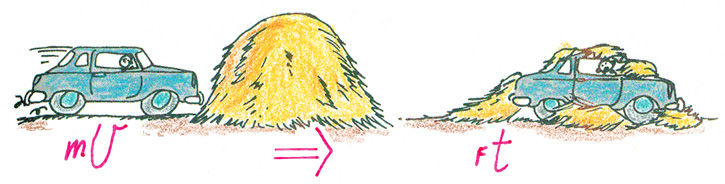
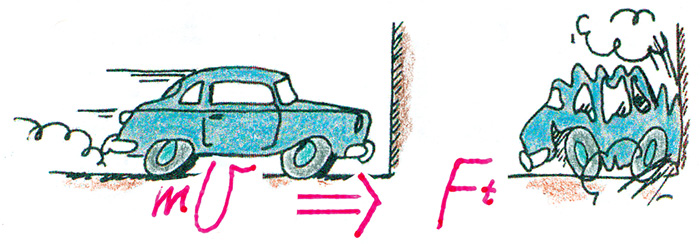
Car crashes and energy conservation

In Figure 2 we see the same car crashes of Figure 1, but analyzed in terms of energy. The work-energy principle tells us that the change in kinetic energy (∆KE) of something, in this case a car, is equal to the work (Fd) done on it. Note that KE reduces to zero whether the car slams into a haystack or a massive wall, which is equal to the corresponding force × distance in each case. It’s nice when more than one physics relationship is useful in answering a question.

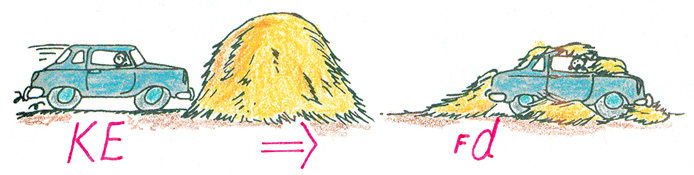
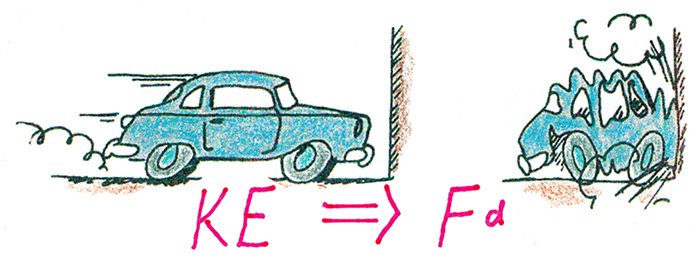
Recognizing parallel situations

A subtler version of the car crashes is hammering a nail into two kinds of wood—soft pine and hard oak (Figure 3). Experience will show that for the same swing of the hammer, the nail is driven farther into a block of pine than into a block of oak. So we ask: “Which nail is hit with the greater force?” Don’t say the same. Compare the hammering examples with the crashes in Figures 1 and 2. Isn’t the soft pine akin to the haystack? And isn’t the hard oak akin to the massive wall? The nail driven into the hard oak is hit with more average force. The soft pine “yields” in the same way the haystack yields: less force, more time, same impulse. Or, less force over greater distance, for the same work done. It’s nice to analyze a situation by more than one route.

Ohm’s law

In electrical experiments in the early 19th century, Georg Ohm made a remarkable discovery about the relationship between what we now call current, voltage, and resistance. He found that when a voltage is applied between two points in a wire or other conductor, the amount of current made to flow is directly proportional to the applied voltage, and inversely proportional to the electrical resistance. The relationship is now called Ohm’s law:

Current = voltage/resistance, or in symbols, I = V/R

The law is often written V= IR, but I find the ratio form I = V/R more intuitively meaningful: More voltage means more current; more resistance means less current. As with most written equations, I encourage magnitudes indicated via different sized symbols.

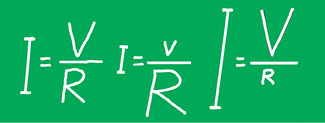
Reading current and voltage

While we’re speaking of current and voltage, let’s be sure your students understand that only current flows, not voltage. And let’s also overlook the redundancy of “current flows.” Strictly speaking, current is the flow of charge. Putting grammar aside, we can say that current flows but voltage doesn’t. Voltage is exerted; it doesn’t flow.

I discussed the redundancy of current flow decades ago with Richard Feynman, who had just critiqued the first edition of my high-school textbook. Feynman said that pedagogically, some redundancy is good. He was okay with the term current flow. I think students are, too, but I don’t write “current flows” in my textbooks. Redundancy works better spoken than written. 

The equation E = mc²

The relationship Albert Einstein saw between energy and mass is expressed by what is probably the most famous equation in all of physics: E = mc². A literal reading of the equation is “energy equals mass times the speed of light squared.” What the equation means is that energy and mass are interchangeable—different forms of the same thing—mass-energy. Mass is a measure of inertia, or “solidity.” Energy is a measure of “activity,” as with moving objects or a flow of radiation. Confined energy has mass. Mass and energy, two forms of mass-energy, are equivalent. 

Why the c²? It fills the role of a “conversion factor,” because mass and energy are expressed and measured in different units—say kilograms and joules. Just as a conversion factor is needed to relate kilometers and miles, or nanoseconds and years, one is needed to relate mass and energy. (In standard units, c = 3 × 10⁸ m/s; c² = 9 × 10¹⁶ (m/s)², which is equivalent to 9 × 10¹⁶ J/kg. So mc² has units kg(J/kg) = J. Hence the unit J for both E and mc².)

In standard units, c² is a very large number, 9 × 10¹⁶ (m/s)². This tells us that only a small change in mass is needed to release an enormous amount of energy, as in a nuclear weapon; and that the changes of mass associated with everyday changes of energy are too small to measure.

Origin of E = mc²

Einstein arrived at his famous equation by considering a moving object that emits light both forward and backward (for example, by a lamp mounted on top of a railroad car). He found that this system of massive object and its emitted light obeyed his new principles of relativity only if the object radiating the light lost a little of its mass.

At that time (1905) no one had yet imagined any conversion of mass to energy, much less its total conversion as when a positron and an electron “annihilate,” but Einstein did suggest that the effect might be detectable in processes of radioactive decay. Most obvious today, the conversion of mass to radiant energy is evident in sunshine.

Solar energy and E = mc²

At Earth’s distance from the Sun, the energy of arriving sunlight is about 1,360 joules per second (watts) per square meter. One can work backward and find out how much total energy the Sun is emitting every second, and then, from E = mc², figure at what rate the Sun is losing mass. It turns out to be 4.5 million tons of matter “lost” to radiant energy every second. The same principle applies on Earth. For every joule of energy sent out over the wires from a power plant, a tiny mass of fuel is lost. It is not too far-fetched to say that mass is being delivered through the copper wires that run from power plants to consumers.

When we find our students juggling symbols in equations, let’s be sure they know the meanings of those symbols. If they learn to read equations as they learn to read words, both their understanding and their joy in physics will grow. That’s good for everybody!

On the web

On www.HewittDrewIt.com are two screencasts for teachers, 148 student-oriented tutorial lessons covering a broad swath of physics, and links to related materials, also on www.ConceptualAcademy.com.

Paul G. Hewitt (Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, new 13th edition; Conceptual Physical Science, 6th edition, coauthored with Leslie Hewitt and John Suchocki; and Conceptual Integrated Science, 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.) is the author of Conceptual Physics, new 13th edition; Conceptual Physical Science, 6th edition, coauthored with Leslie Hewitt and John Suchocki; and Conceptual Integrated Science, 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.