Cartoons often convey ideas more quickly and effectively than the written word alone. We’re all familiar with political cartoons that can capture the essence of a long discussion; the same can be true with the concepts of physics. This article presents some of the cartoons I’ve created for future editions of my textbooks, shown here first. 

Course coverage

As physics teachers we must sort through a vast amount of material to teach the essentials of physics. Thoroughly covering all topics isn’t possible. Hurrying to attempt to do so often ends with catastrophic results. In my view, once a manageable number of topics has been selected, it’s important that an introductory physics course presents the central laws of physics as the study of nature’s rules.

Nature’s rules

The laws of physics and nature’s physical rules can be viewed as one and the same. Our mascot Manny Mouse illustrates this unity with the equilibrium rule in Figure 2, which is an application of Newton’s first law of motion. It’s a remarkable rule, stating that all the forces acting on anything at rest (or moving uniformly) cancel to zero. This rule of nature is central to all structures—bridges, skyscrapers, and even the trees in our forests.

Distinctions

A course in physics can highlight two essentials. The first is to show how concepts connect. Such connections are guided by equations that are best read for meaning long before being used to solve numerical problems. The second is distinguishing between closely related concepts. This occurs early in most physics courses with the distinction between speed and acceleration, which Suzie Sailor summarizes in Figure 3.

Another important distinction is between mass and weight. Mass has to do with inertia of stuff—its resistance to acceleration (Figure 4). Weight has to do with the gravitational pull on stuff.

The most central rule

Newton’s second law is central to all motion (Figure 5). Centuries ago, Galileo defined acceleration as a = ∆v/∆t. That’s what acceleration is. Newton told us how it comes to be: a = F/m. Newton’s second law of motion was the primary law responsible for putting a man on the Moon in 1969.

The question most frequently missed in a physics course involves the acceleration of a vertically projected ball at the top of its path (Figure 6).

The most common answer is zero, which is incorrect largely due to the common confusion between velocity and acceleration. Velocity at the top is certainly zero—for a moment. But does this mean the rate of change of velocity is also zero? Certainly not. The force due to gravity (mg) that slowed the ball still acts on the ball. Likewise, its mass remains the same. And what is the ratio of force to mass? Isn’t that acceleration as per Newton’s second law? Guiding thinking, we see that  a = F/m = mg/m = g.

The misunderstood rule

Newton’s third law, the law of action-reaction, is the most misunderstood of his three laws of motion (Figure 7).

A key idea in the third law is that the forces involved are simultaneous. An action today followed by some reaction tomorrow is therefore not governed by the third law. Newton’s third law applies only to pairs of forces that occur simultaneously. If action is a force exerted by body A on body B, then reaction is body B simultaneously exerting an equal and opposite force on body A.  Quite interestingly, you cannot exert a force on something unless that something simultaneously exerts an equal and opposite force on you. That’s a central law of nature. Hence you cannot touch without being touched, as author and wife illustrate (Figure 8).

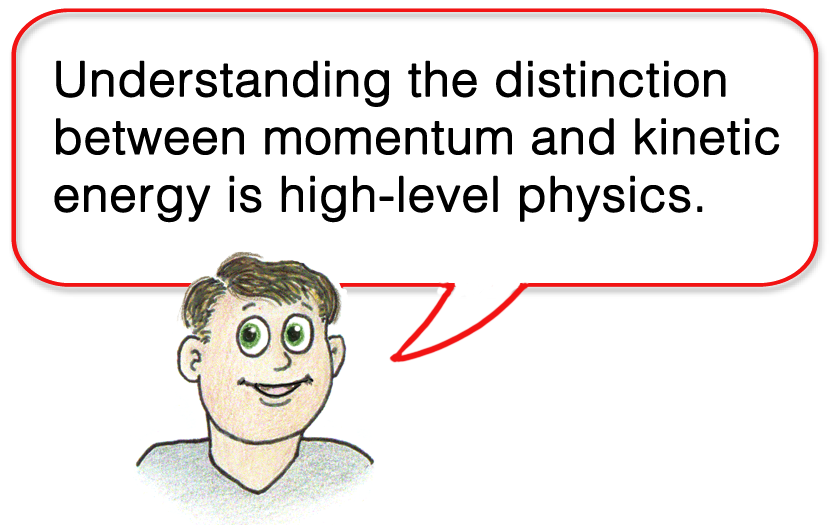
Impulse and momentum

Newton dealt with momentum in his writings, for the concept of energy was vague in his time. In fact, the law of conservation of energy followed Newton by more than a century.  His phrasing of his second law was in terms of momentum, the vector quantity mv. A rearrangement of Manny Mouse’s statement in Figure 5 can be expressed as what we now call the impulse-momentum relationship (Figure 9).

When you push on something you exert a force. How much momentum changes depends on the impulse—the force multiplied by the duration of the push. The impulse F∆t exerted on a body of mass m proportionally changes its momentum mv.

A basic difference between momentum and energy is that momentum is a vector quantity and energy is not. Momentum, not energy, can be cancelled in interactions. You may be able to cancel the momenta of exploding firecrackers tossed into an enclosure, but never their energies. 

Work

A close cousin to impulse, but an entirely different concept, is work, the action of a force exerted on a body over a distance d; W = F∆d. Impulse and work are another pair of concepts that are often confused. Distinguishing between them is important. Impulse, I = F∆t is entirely different from work. When we consider the effect of a force exerted on something over a distance, we’re talking about work (Figure 11). The work done on an object can change its kinetic energy.

All the equations of physics are guides to clear thinking, and both the concepts of impulse-momentum and work-energy are widely used by students in solving mechanics problems. Both are also physics prisms to view situations where changes in motion occur.

Central to all science is the conservation of energy (Figure 12).

Rotation

Rotational motion is often a topic excluded from a physics course when the goal is wide coverage, getting to rainbows and beyond. The essence of circular motion, however, is a simple one: relating tangential velocity v to angular velocity ω.

To avoid getting bogged down with radian measurement of angles, the equation v = rω can be expressed as the proportion, v ~ rω. The proportion form allows angular velocity to be expressed in familiar rpms, revolutions per minute (Figure 13).

In all areas of study, being able to explain what you’ve learned is paramount (Figure 14).

Gravitational Force

In our spacefaring age, Newton’s law of gravity is quite relevant (Figure 15).

Gravity is the force that both holds us to the ground and holds satellites in orbit around Earth. For satellite motion, it’s important to stress the symbol r, denoting the distance from a center of gravitational force. Those who think that the International Space Station (ISS) is in a gravity-free zone, zero-g, are challenged when confronted with the small difference in r at Earth’s surface and in satellite territory. The ISS experiences some 93 percent of the force of gravity on Earth’s surface (which keeps it from flying off into space in a straight-line path). Equations guide good thinking (Figure 16).

We conclude with a cartoon that nicely illustrates an idea that applies generally, especially in this time of a changing world climate. 

Next month’s Focus on Physics will extend cartoons to physics topics beyond mechanics.

On the Web

See complementary student tutorial screencasts on www.HewittDrewIt.com, and on www.ConceptualAcademy.com. 

Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, 12th edition; Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, new 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.