Focus on Physics
Aha! Moments When Teaching Acceleration
The Science Teacher—November/December 2022 (Volume 90, Issue 2)
By Paul G. Hewitt
Teaching acceleration is decidedly a bigger challenge than teaching speed and velocity. That’s because speed and velocity are intuitive, while acceleration is not. Maybe it’s fine to hurry through speed and velocity, but teaching acceleration should be allotted additional time. How to teach it is featured in my March 2019 Focus on Physics article “Quickly Teaching Speed, Velocity, and Acceleration—Part 2.” This article extends that by highlighting some of the gems associated with teaching acceleration. We begin with Galileo.
Galileo and acceleration
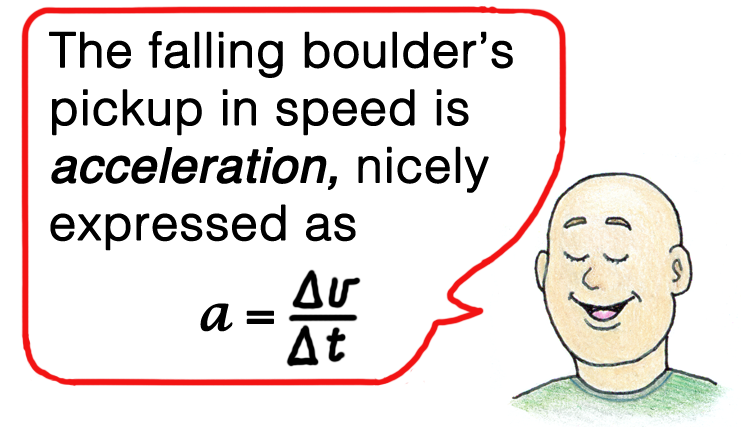
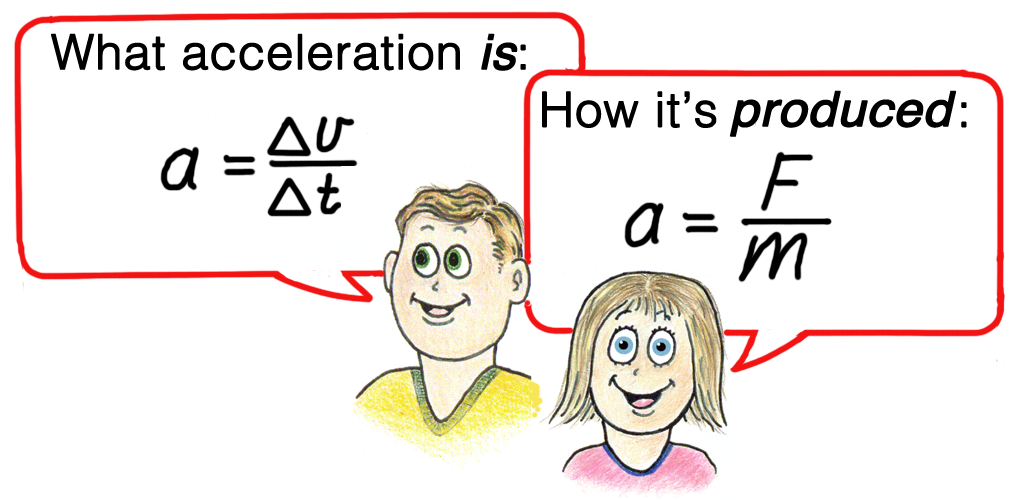
Galileo was the first to introduce the concept of acceleration. He defined velocity as the time rate of change of distance, and further defined acceleration as the time rate of change of velocity. The challenge for students is coming to terms with the idea of “time rate of change.” We introduce the symbol ∆ (delta) to denote “change in.” A change in velocity is expressed ∆v; a corresponding change in time is ∆t. We can express the equation for acceleration as a = ∆v/∆t, which is read: Acceleration is equal to the change in velocity per change in time. Maybe a small aha! if students can articulate this, and go further and and say what it means.
Falling speedometer
I’ve found that a great way to visualize acceleration is imagining a speedometer attached to a boulder dropped from the edge of a high cliff, which I featured in the March 2019 Focus on Physics article (Figure 1). Only the force of gravity acts on the boulder and its speedometer; without air drag, it is in free fall. Dropped from rest, the initial reading is zero. One second later the reading is 9.8 m/s, which we’ll round off to 10 m/s (multiples of 10 are easier to handle). In two seconds the speedometer reads 20 m/s. In three seconds, 30 m/s, and so on. Ask your students what the change in speed is during each 1-second interval of fall. This represents another small aha! moment, for it’s easy to see a 10-m/s increase for each second of fall.
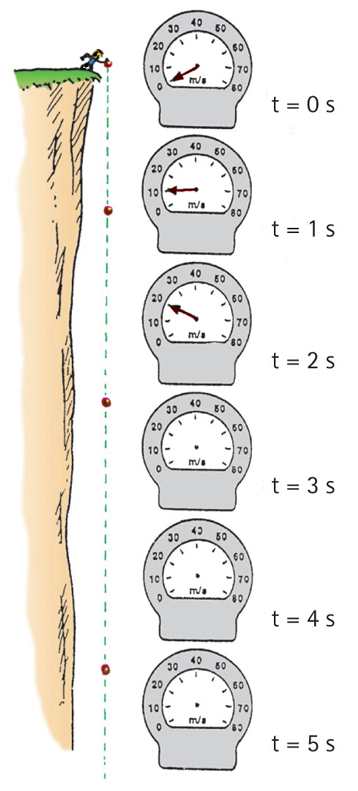
The freely-falling speedometer gains the same amount of speed each second.
Expressed in delta notation, for every ∆t of one second the gain in speed ∆v is 10 m/s. So what’s the value of ∆v/∆t for the falling boulder? Another Aha! It’s 10 m/s per every 1 second. We can express this as 10 m/s per second, or, 10 m/s/s, which is read as 10 m/s squared, or in math notation, 10 m/s2. Again, to simplify calculations, we round free-fall acceleration that is customarily expressed as 9.8 m/s2 to 10 m/s2. During each second of free fall, the exact same pickup of speed occurs. We say the boulder and speedometer fall with constant acceleration.
Meters per second squared
You can expect that some students will be uncomfortable with the symbol for second appearing twice in m/s2—first for velocity and again for the time that velocity changes. Hence the second squared. Or, remind them of a rule of arithmetic that says when dividing a fraction by a number (m/s ÷ s), invert the number and change the division sign to a multiplication sign. Then you have m/s × 1/s = m/s2. If you still have some puzzled students, my advice (nurtured by many years of teaching) is to NOT devote more class time to it. In the spirit of “wisdom is knowing what to overlook,” tell your class that in their study of physics, for some students, all will not be fully understood, and that to keep on your scheduling quest to advance to other physics goodies, you’ll not spend time on what could better be spent in a math class. Move on! An aha! is that your course can get up to rainbows and other physics goodies before the course-time bell rings!
A follow-up to speeds of fall is assigning an odometer to the falling speedometer. Then you can treat the distances covered in free fall.
Why?
Why objects accelerate is answered by Newton’s second law, sometimes called the law of acceleration. It tells us that the acceleration of an object is directly proportional to the net force on the object, and is inversely proportional to the mass of the object. In summarized form, this is
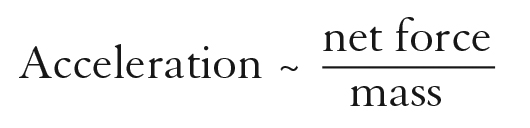
With appropriate units of a, F, and m, we can express this as the exact equation:
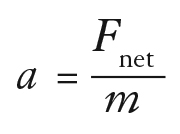
The acceleration is always in the direction of the net force.
The gems are found with its applications. For example, the acceleration of the falling speedometer of Figure 1 is a constant, whatever its mass. We know a feather and a rock will accelerate equally in a vacuum—when air drag is negligible, any two different-mass balls will fall with equal accelerations, g. Whatever the mass, gravitational net force mg, divided by m, equals g (Figure 2).
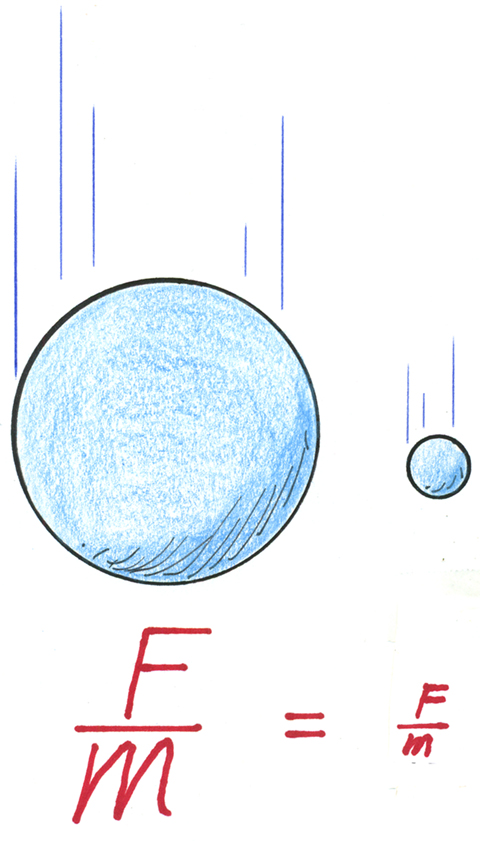
Why does the heavier ball not fall faster than the lighter ball?
Acceleration examples
The equation a = F/m tells us why an automobile with a full tank of gas will accelerate less then when the tank is nearly empty. For the same applied force, greater mass means less acceleration. This physics is enormously important for rockets. Their initial mass before launch is mostly the mass of its fuel. Initial acceleration is sluggish, but with time, fuel turns to exhaust and the mass of the rocket decreases with a correspondingly increasing acceleration that puts it into orbit. A big aha! Now we know why rocket launches that seem so slow gain enormous speeds when high and out of sight.
Acceleration “at the top”
Distinguishing between related concepts is a challenge in physics. One such distinction is between velocity and acceleration. A test question for understanding this distinction is this scenario with a tossed pet (Figure 3): What is the acceleration of a vertically tossed pet dog at the top of its path? The common response is zero. An aha! is awarded to those students who correctly and rarely answer g. More students will answer correctly if the question is posed: What is the acceleration of a vertically tossed pet dog at the top of its path at the moment its velocity is zero? How you ask a question influence how it is answered.
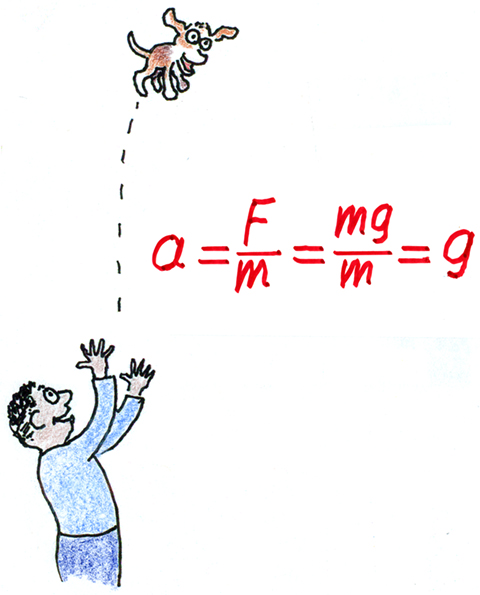
Figure 3. What’s the pup’s acceleration at the top of its trajectory?
If zero, then what?
In my decades of teaching, I find this question the most incorrectly answered the first time it is presented. I think most teachers and professors would agree. I’ll always remember my first exposure to this question on an exam in my undergraduate years when Professor Block wrote a large red X over my wrong answer—to my disbelief. Professor Block asked “if both acceleration and velocity are zero, then what?”—an unforgettable gem and a bright aha! moment. Follow your explanation with this punch line: Speed and velocity are not acceleration, which is the time rate at which speed or velocity undergo change. No change, no acceleration!
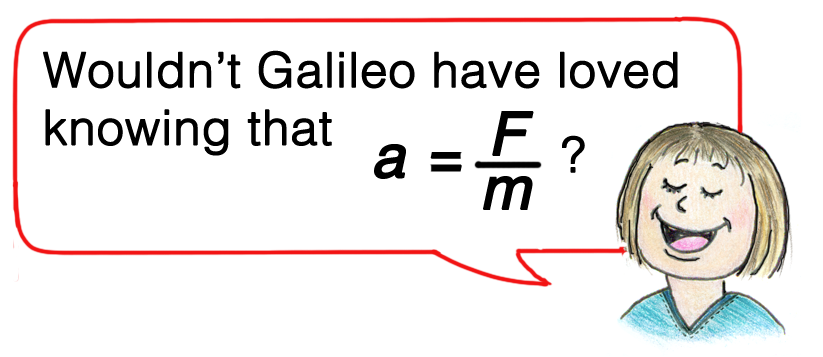
Learning
We began with the acceleration of the falling speedometer. Galileo told us what acceleration is, Newton told us how we get it. We learned that if the only force acting on a falling object is gravity, then whatever its mass, its acceleration is g. And we’ve learned to distinguish between the closely-related ideas of velocity and acceleration.
Central physics topics
These topics are central ones. Most dedicated teachers will emphasize them. Some others, perhaps not. I think of my physics friend and colleague Dave Wall, also an amateur magician, who delights in pulling pennies out of children’s ears. When bystanders ask why he doesn’t tire of doing so, Dave replies that he doesn’t tire of it because each time it’s with a new kid. Similarly, we may be asked if we tire of teaching the fundamentals of physics over and over, term after term. Wouldn’t it be more interesting to teach the latest findings in physics with our classes? Or show off our latest method of solving algebraic problems? I’m with Dave Wall: Each semester we’re committed to teach physics fundamentals, and the beauty of it is that we do it each term with a new class. If we don’t teach the physics, then who will?
On the web
For more on acceleration see tutorials 18 – 23 on www.HewittDrewIt.com. Also are two screencasts for teachers, 148 student-oriented tutorial lessons covering a broad swath of physics, and links to related materials. See also www.ConceptualAcademy.com.
Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, new 13th edition; Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.
Physical Science Physics High School


