Equations are important in a physics course, whether it’s oriented toward science and engineering students or nonscience students in a survey course. For physics students at all levels, equations—when viewed as shorthand statements of nature’s rules—should not be minimized or avoided. Rather than being used as recipes for working algebraic and numerical problems, equations best serve as guides to thinking. Minimizing number crunching and placing greater emphasis on the meaning of the symbols in equations can be a breath of fresh air for most students. 

Let’s begin with Newton’s universal law of gravity in proportion form: 

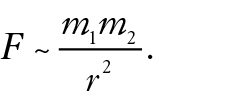
Gravitational force 

Introduce the proportion and discuss its symbols, noting in particular that r (sometimes written d) represents the distance between the centers of mass of the objects. After discussing the historical importance of this proportion, pose a series of questions. Ask what change occurs in the force between two planets if the distance between them is doubled? Tripled? 

Then go the other way: Ask about the force when the distance between planets is halved. Decreased to one-third? Then ask how force is affected when their masses are increased or decreased. And so on. Encourage them to answer out loud (assuming your classroom doors are closed). Learning that takes place in your class may be indicated by its noise level—one of delight. You are teaching your students to read equations and impart meaning to their symbols. Your students are learning the mathematical foundations of physics without crunching numbers. Your students are enjoying themselves.

More questions

Does the attractive force between a pair of planets in space depend on their color? Their temperature? The answers are no, for there are no terms for color or temperature in the proportion. Color and temperature do not affect mass or distance between the planets. Does the speed of a planet affect the force acting on it? We see that symbol v isn’t in the proportion, and there is no compelling reason to expect speed to affect mass (excepting special relativity). Unless v affects distance r, then speed isn’t involved. The point of these questions is to see that an equation’s symbols tell us what does, and what doesn’t, affect gravitational force. 

Gravitational constant G

About a century after the time of Newton, careful measurements of gravitational force in the laboratory showed that for a pair of masses at a precisely measured distance, the ratio of gravitational force F to the product of their masses divided by distance squared produced a number that we now know to be, 6.67 × 10^-11 N·m²/kg² (SI units), which we call the universal gravitational constant G. The proportional formula for gravitation becomes the exact equation 

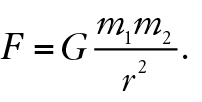
Helpful analogies 

New knowledge is best learned when it is analogous to familiar knowledge. Your class likely knows that the circumference of a circle C divided by its diameter d always produces the same number, 3.14, which we call π. C/d = π for all circles. Likewise, G is the same for all bodies that attract gravitationally. 

Celebrating science

In the eighteenth century, when G was first measured, people across the globe were excited about it. Newspapers everywhere announced the discovery as the measurement of the mass of planet Earth. With all its oceans, mountains, and inner parts yet to be discovered, Newton’s equation gives the mass of Earth. Previous to G, the law of gravitation was a proportion, allowing comparisons of forces. With the exact equation, forces could be expressed in their units, newtons for example. 

The Newtonian synthesis

The legend of Newton and the falling apple has historical support. As an old man, Newton told friends that the universality of gravitation occurred to him when he saw an apple fall from a tree in his mother’s garden many years earlier (Figure 1). He had the grand insight that the downward force on the apple is the same as the force holding the Moon in its orbit around Earth, and furthermore, the force holding Earth in its orbit around the Sun. This insight is called the Newtonian synthesis—the union of terrestrial and cosmic laws.

Figure 1. The Newtonian synthesis began with a falling apple. 

Physics equations are universal

When your course gets to Coulomb’s law, which is very close in form to the law of gravitation, a briefer but similar set of questions will extend the value of being able to read equations. For now, however, let’s skip ahead to Georg Ohm and the law that bears his name.

Georg Ohm

The life of Georg Ohm, a German physicist, mathematician, and teacher who discovered the law in the 1820s makes an interesting story. His hobbies in youth included dancing, ice skating, and playing billiards. These nonacademic activities didn’t please his strict father, who sent him to Switzerland, where at age 16 he became a math teacher. He continued his studies of mathematics, his main passion, and earned a doctorate at the age of 22. He wrote a book on elementary geometry that impressed King Wilhelm III of Prussia, who offered him a teaching position in Cologne. It was there that his passion switched to physics. In Cologne’s well-equipped lab, he found a remarkable relationship between voltage, electric current, and electric resistance. 

Ohm’s law

Traditionally, Ohm’s law is presented as V = IR. This plug-in formula is not very enlightening. Think how much better the student will “get” the meaning of the law if it is written

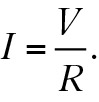
Voltage is an electric pressure in a circuit. Therefore it makes sense that more voltage means more current (I ~ V) and more resistance means less current (I ~ 1/R) (Figure 2). So, just as Newton’s second law is often more meaningful when expressed as a = F/m, Ohm’s law is better understood as I = V/R. Ratios of concepts make good pedagogical sense.

Your students will probably be amused (and Ohm himself would no doubt have been amused) to learn that the inverse of resistance, called conductance, was assigned the unit mho (pronounced MO), or ohm spelled backwards. The SI unit, however, is the siemen. Real-life examples of Ohm’s law include birds sitting unharmed on high-voltage wires, a person walking unharmed on the third rail of an electric train, but harmed indeed if one foot touches the ground—and the inadvisability of using electric appliances in the bathtub.

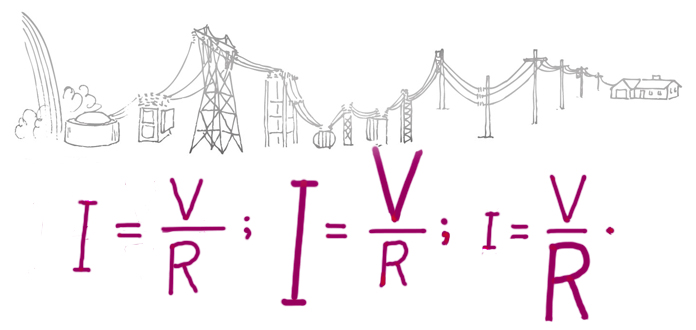
Figure 2. Current is greater when voltage is greater. Current is less when resistance is greater. 

Max Planck

As a youth in Germany, Max Planck was a gifted musician who became enamored with physics and earned his doctorate in 1879 at age 21. In 1900 he hypothesized that the emission of radiant energy from matter is not continuous but is in discrete amounts or lumps, which he called quanta. He also proposed that the quantity of energy in each quantum is proportional to the frequency of the radiation. Five years later Einstein took the next step, proposing that light itself exists as quantum lumps or “corpuscles,” later named photons. 

Photons

Light is emitted by atoms when their electrons jump from one energy level to another. The carriers of light are photons, which we envision as throbbing corpuscles of vibrating energy. The energy carried by each photon is proportional to its frequency of vibration, E ~ f. The constant of proportionality (dividing E by f) is Planck’s constant, h, named in honor of Max Planck. So, 

E = hf.

Relevant number crunching

Isn’t relating this equation to the photon energy emitted by smartphones (Figure 3) a better case for introducing numbers than kinematic number crunching at the beginning of your course? Your students could find out, for instance, that the low radiation frequency (relative to the frequencies of ultraviolet light or X-rays) means correspondingly low energy for each photon of radiation emitted in a mobile phone—energy that is far less than is needed to eject an electron from an atom.

Figure 3. E = hf : Radiant energy emitted by a smartphone. 

Energy and DNA

Some numbers are of value here. When photons transfer energy to a material and break chemical bonds, they can dislodge one or more electrons from an atom in the material. This is ionization, which can cause cell damage. Damage to DNA in our cells is serious and can lead to cancer. The minimum energy to damage DNA is at least 4 electron volts per photon. This corresponds to a radiation frequency of 10¹⁵ hertz, about tens of thousands of times greater than the microwave frequencies of mobile phones. So we learn that the photons that make up mobile phone radiation are only a tiny fraction of an of an electron volt per photon. Although mobile phones continue to be tested for adverse health effects, how nice that your students know that the radiation associated with mobile phones cannot produce the ionization that causes cancer. 

Course coverage

Mechanics, heat, and electromagnetism are the most “equation heavy” topics in introductory physics. Some teachers therefore opt to begin a course with waves, light, and color. For students intimidated by equations, this makes pedagogical sense. The “more-math” part of the course is then postponed until confidence in learning physics has grown. I make the point that an early introduction of carefully explained equations can also work. The important thing is to focus on the meaning of equations, and to treat them as guides to thinking. 

It is also important to remember that when most of the facts, diagrams, and equations have been forgotten, the flavor of your course will linger. It should be a positive one. You can help to make it happen by teaching equations—the rules of nature—in a meaningful way. ■

On the Web

See complementary student tutorial screencasts 16, 19, 45, 91, and 121 on www.HewittDrewIt.com, and on www.ConceptualAcademy.com. 

Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, 12th edition; Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, new 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.