focus on physics
Calculating Distances Via Flagpole Shadows
The Science Teacher—September/October 2020 (Volume 88, Issue 1)
By Paul G. Hewitt
In the February 2020 issue of The Science Teacher, my article “Measuring Shadows to Calculate the Size of Earth” examined Eratosthenes’ 240 BC achievement in measuring Earth’s circumference. In the concluding paragraph I suggested reversing the process—to use Earth’s circumference as a known quantity to find the unknown distance between far-apart flagpoles. Assuming that every school has a flagpole, I want to guide student calculations of distances between far-apart schools. A meterstick and a smartphone are all that are needed.
Shadows
Any vertical structure in sunshine casts a shadow. We’ll focus on the shadows cast by flagpoles. The length of the shadow depends on the height of the flagpole and the angle of incident sunbeams. That angle and its corresponding shadow will vary throughout the day due to the Sun’s apparent motion in the sky. Due to Earth’s curvature, the shadow cast at one location at a given time will differ from the shadow cast by another flagpole at a distant location at the same time. (Figure 1).
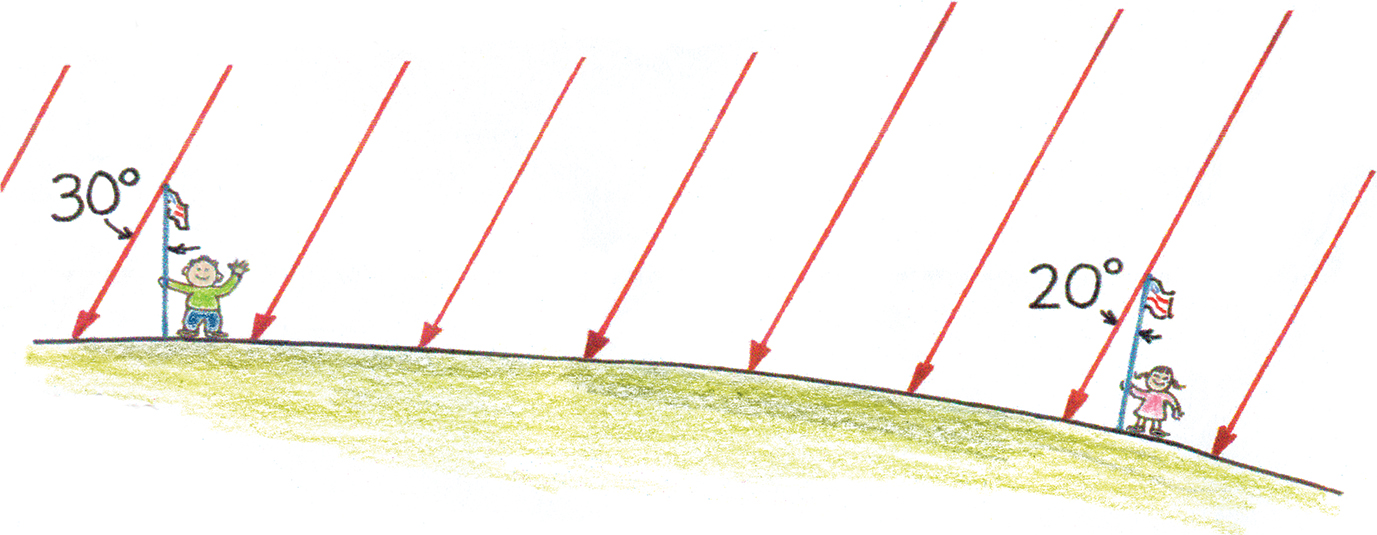
Flagpoles in sunlight cast shadows
Distances
We’ll explore a fascinating connection between flagpoles in sunlight and the distance between those flagpoles. The distance may be between a school in one state and a school in another state, or between flagpoles on far-apart islands such as in Hawaii. Simple measurements and calculations of such distances present an interesting cooperative activity for students in different locations. The distance between two teams of student investigators is the arc distance subtended by some angle at Earth’s center—a distance that relates to their common great circle.
Great circle
A great circle is the largest possible circle that can be drawn through any two points on a sphere such as is approximated by Earth. Figure 2 shows examples of great circles. One great circle at the equator is shown in red. Another, along a line of longitude, is shown in blue. A random great circle is shown in green. Again, any two locations on a sphere define a great circle. There are an infinite number of great circles about Earth. What they have in common is that they all have centers at Earth’s center.
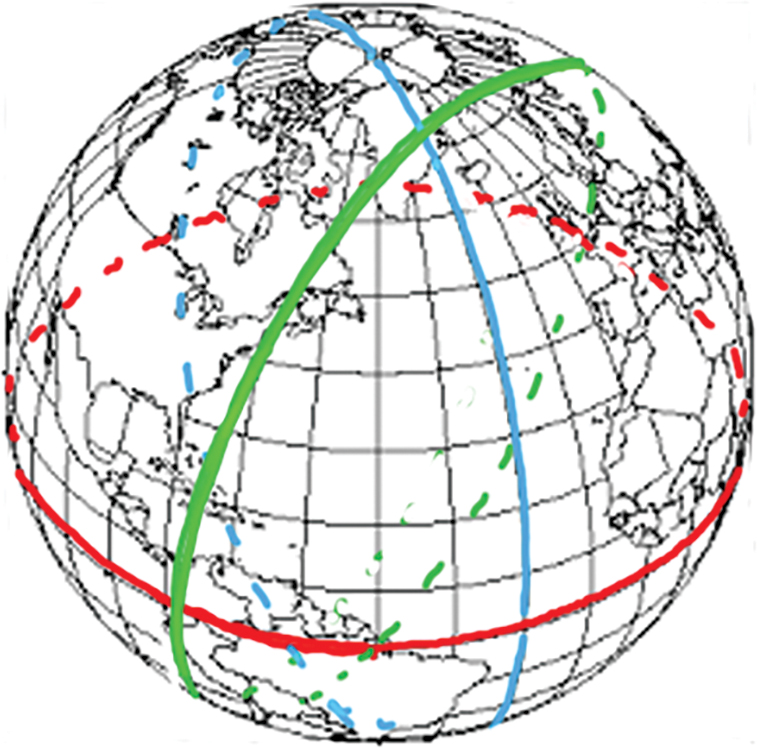
Three examples of great circles.
Flagpole locations
A point at one team’s location and a point at the second team’s location define a great circle. That’s right, the teams occupy two points on their common great circle. If imaginary vertical lines are extended beneath each of the flagpoles, they will intersect at Earth’s center at an angle α (Figure 3).
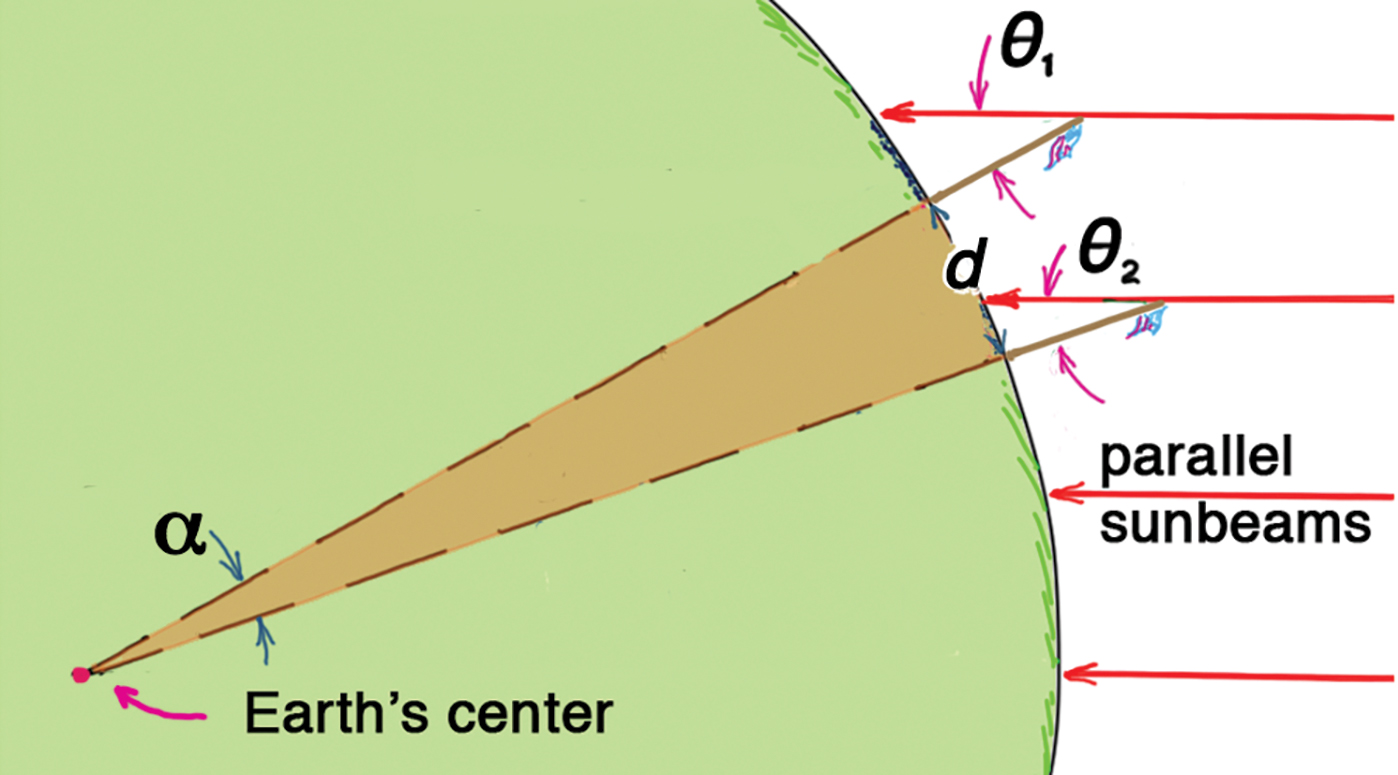
Extended vertical lines beneath two flagpoles form an angle α at Earth’s center
A piece of pie
If angle α were known, it would be easy to calculate the arc distance d between the flagpoles. Think of the tan-colored sector in the figure as a piece of pie. How many such pie pieces are needed to make up a whole circle (a whole “pie”)? The answer is 360°/α°. So that number of “pie pieces” multiplied by distance d is Earth’s circumference. Turned around, the known circumference of Earth divided by the number of pie pieces is the unknown distance d. So students need to determine α. Here’s where the shadows cast by the school flagpoles come into play.
Flagpole shadows
We are not interested in random shadows cast by flagpoles. Our concern is flagpole shadows that specifically fall along the two-flagpole great circle, which occurs when the shadow at one flagpole points directly to (or directly away from) the other flagpole. When that occurs, the sunbeams will be parallel to the plane of the great circle (Figure 4). Only then will α directly relate by way of simple geometry to the sunbeam angles θ1 and θ2 at the flagpoles.
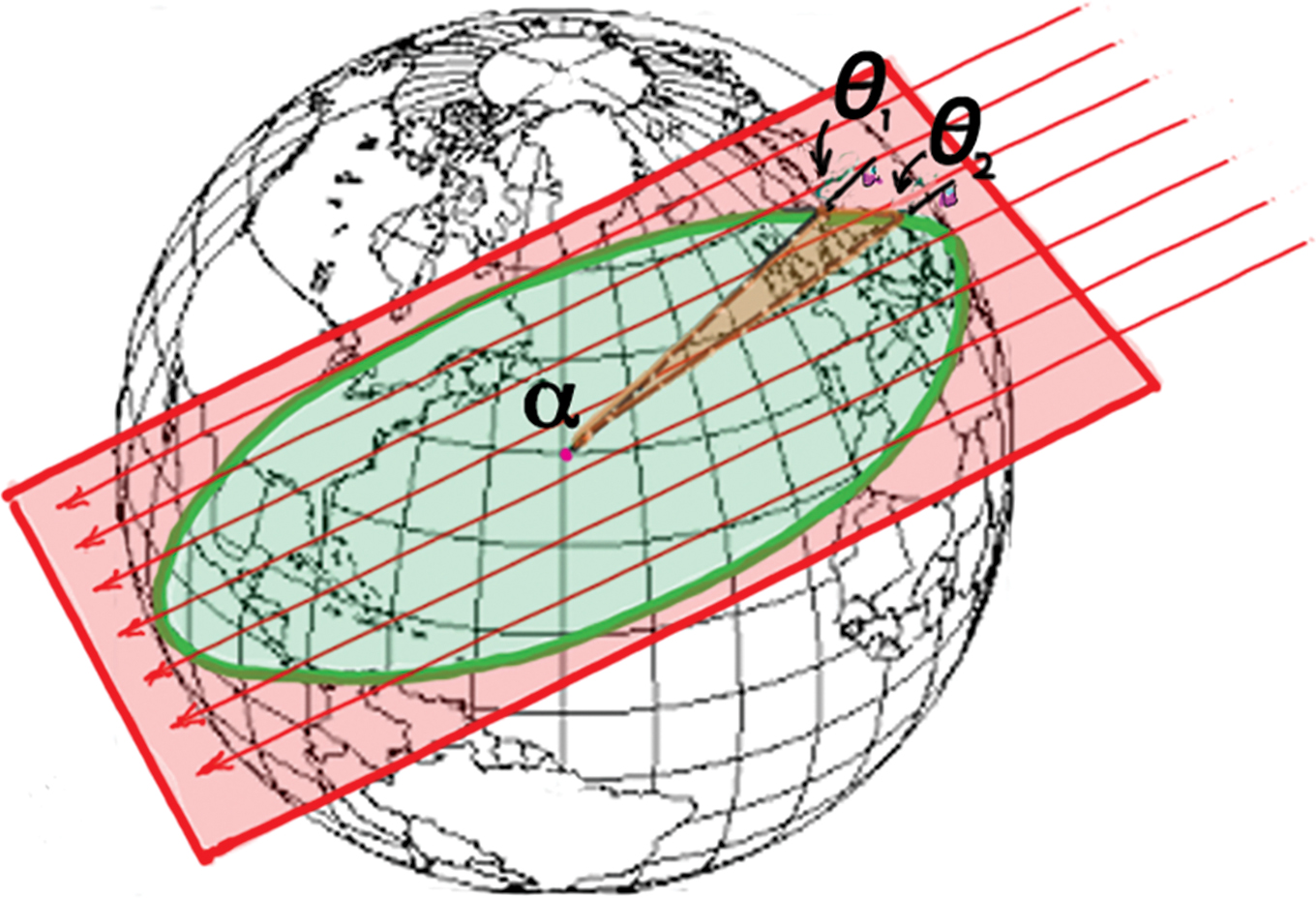
When the plane of the great circle and sunbeams are parallel, θ1 - θ2 = α
At that special time, α at Earth’s center will be equal to θ1 – θ2. (When the Sun is directly above a point between the two locations, the shadows point away from each other; α is then equal to θ1 + θ2.) When flagpole shadows do not fall on the great circle the difference in (or sum of) angles θ1 and θ2 will not equal α at Earth’s center. Then spherical trigonometry is required. Fortunately, the special condition where plane geometry suffices occurs more often than you might think.
Timing
Anywhere on Earth, with rare exceptions, the shadows of a pair of vertical structures in sunlight will align along their great circle at some time on some day. The students’ task is to find a date and time when the shadow cast by one school flagpole points directly toward or directly away from the flagpole in the other location. Numerous smartphone apps provide the latitude and longitude at each location, and there are web sites that enable students in each location to find the direction toward the other location.
This direction should be somehow “marked”—perhaps by some feature that lies in the direction of the sought-after shadow. When the shadow falls along the predicted direction (along the great circle), a measure of its length compared with the flagpole’s height yields the angle θ1. Simple trigonometry makes this easy to do. Measurements at the other flagpole should occur at nearly the same time. The lengths of the shadows change slowly, so timing needn’t be exactly simultaneous.
Numerical example
Suppose at the time when the flagpole shadows align with the two-flagpole great circle, one team calculates a 20° angle for the sunbeams at their flagpole. This is where a phone connection between the student teams is important. Further suppose that the first team alerts the second team, and those students calculate a 30° angle with the sunbeams at their flagpole. Going back to our piece of pie, the difference in angles ∆θ is 30° – 20° = 10°, which coincides with α at Earth’s center (Figure 5). Dividing the whole pie by 10° gives us 36 pieces of pie. Dividing Earth’s circumference by 36 gives us the distance d between the two flagpoles: 40,000 km/36 = 1,111 km. More conservatively, because of measurement uncertainties, you could say that the schools are about a thousand kilometers apart.
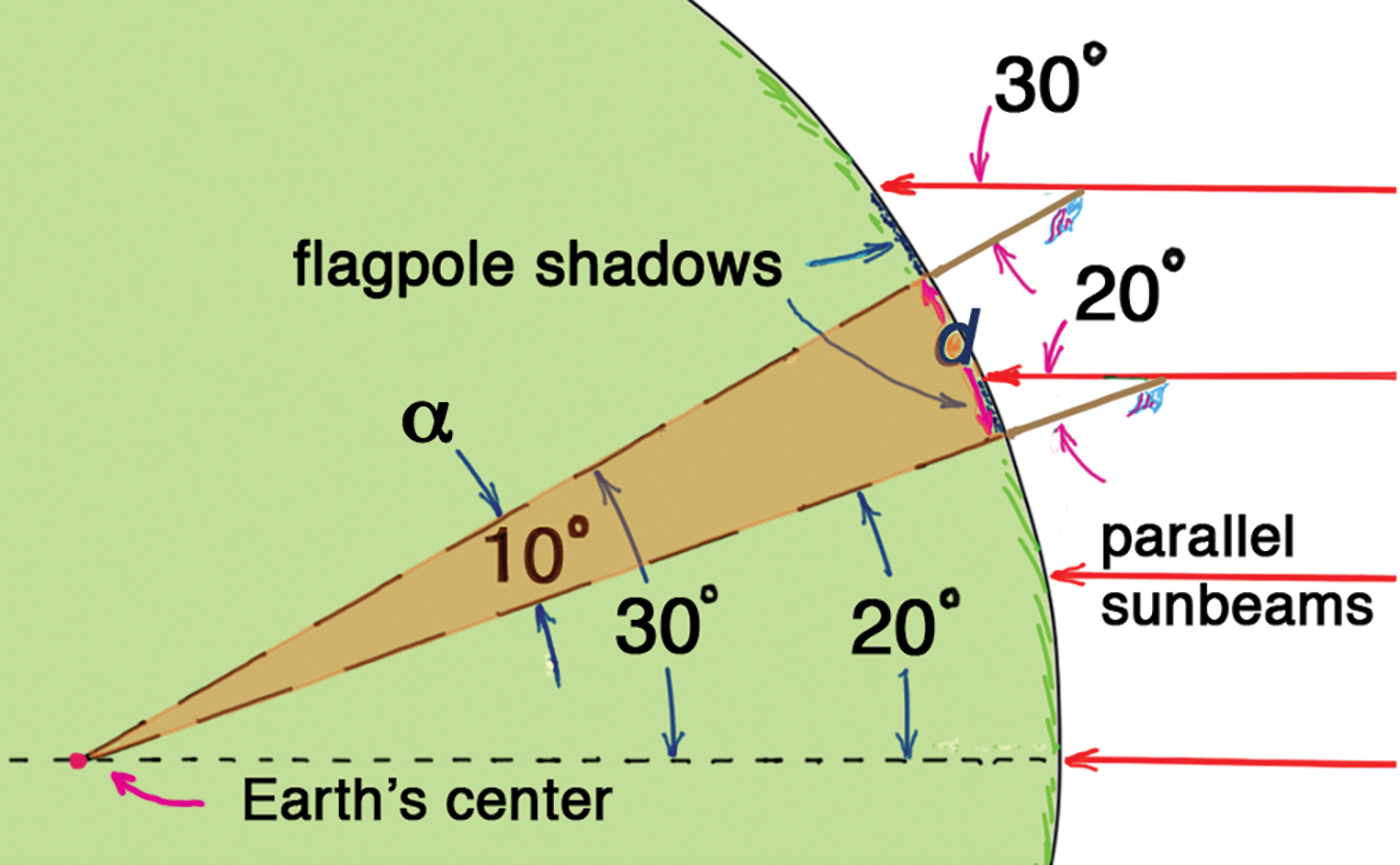
Numerical view
Wrapping it up
In summary, the activity begins with finding the direction from one flagpole shadow to a distant flagpole. This is the direction in which (or opposite to which) the flagpole shadow should point when the sunbeams that strike the flagpole are parallel to the plane of the shared great circle. At that special time, each team calculates the angle that sunbeams make with their flagpoles. Students then find the difference (or, in special cases, the sum) of these sunbeam angles. What fraction is ∆θ of a complete 360° great circle? That fraction of Earth’s circumference is the distance between the flagpoles. With a bit of arithmetic, mission accomplished.
This is a purposeful and cooperative student activity. The time waiting for the shadow of the flagpole to fall along a predicted direction will challenge student patience. If the weather is cloudy or rainy, or if it’s a weekend, just a little more patience is needed. Very nearly the same conditions will apply for several days running. After that, the rest is easy! Go for it!

Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, 12th edition (and upcoming 13th edition in early 2021); Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, new 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.


