Over the years at professional physics meetings I’ve cringed when encountering teachers pleading for ways to make physics more interesting. Whoa! Isn’t physics jam-packed with fascinating nuggets of information? And isn’t physics, the study of nature’s rules, greatly relevant to daily life? If a physics course is seen as uninteresting, perhaps the culprit is the way it’s taught. This can be corrected. To boost class interest, it is important that high-interest nuggets of physics be clearly presented—with gusto.

Delightful gems

A nugget of high-interest information can be thought of as a “gem.” A physics course is ripe with them. Whatever the means of delivering information, gems can and should be presented with a gusto that can elicit “aha!” moments in students. Sadly, even the most interesting gems fall short of the appreciation deserved when emphasis on them is missing.

A potential gem

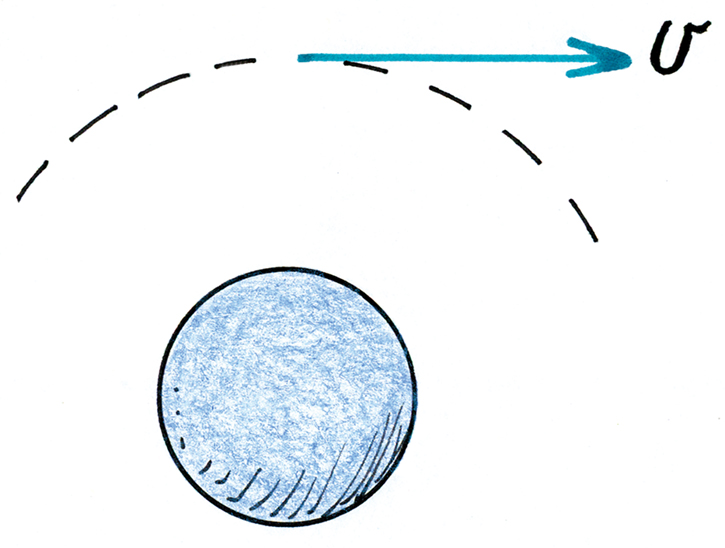
Several years ago Steve, a struggling new teacher, approached me asking my advice in giving a short talk to physics teachers he hoped to impress. An analogy that occurred to me was a lecture I had given on rotational motion, preceded by a student discussion of a well-publicized launch of the space shuttle. My presentation included the popular demonstration of vertically swinging a bucket of water at arm’s length overhead without a spill (Figure 1). I realized the circular motion of water in the bucket is akin to the circular motion of a satellite in orbit. Aha! I suggested that Steve perform the bucket-swing demo, but go further and relate it to satellite motion.

The “trick” of this demonstration is to pull the bucket down as fast as the water falls so the water and the bucket both travel in unison—too slow a swing results in a wet teacher. Although the bucket swing and its explanation would be known to Steve’s audience, I stressed he emphasize that both the water and an orbiting satellite are continuously falling—at just the right speed for the water, and at just the right speed for a satellite to match the curvature of Earth’s surface. Articulating an emphatic connection of these two ideas would surely impress his audience.

A lost gem

But Steve blew it. During his explanation his voice dropped. There was no emphasis whatever on the connection to satellites. He instead nervously mumbled in a monotone that the circular path of the water-filled bucket is akin to the path of a satellite following Earth’s curvature. Mumbles and barely audible delivery don’t elicit aha! moments.

The point of this story is to acknowledge the importance of enunciation and timing. With poor delivery, the best of ideas can fall flat. The gems that follow in this article can elicit aha! moments only if articulated with bold emphasis. Being able to communicate gems with proper emphasis characterizes a successful teacher. (I’ve lost touch with Steve, who was beginning his teaching career. Few of us, including myself, don’t always start with a bang. Teaching skills are acquired with patience and experience.)

Falling satellites

The water in Steve’s bucket was forced to curve by his swinging motion. Similarly, the path of a satellite in orbit is forced to curve by gravity. This is a great analogy. Your students have learned earlier that when only the force of gravity acts on an object, that object is in a state of free fall. Likewise with Earth satellites that are in the grips of Earth’s gravity. They’re all in a state of continuous free fall.

Then comes the common question: Why don’t they crash to Earth’s surface? The answer involves tangential velocity: Each satellite has a tangential velocity great enough to send it over the horizon and continually miss hitting Earth’s surface. Satellites fall beneath the straight-line path they’d experience if there were no gravity. Your wrap-up punch line: Yes, satellites are falling, but they fall around Earth rather than into it. (Be sure to emphasize “around.”)

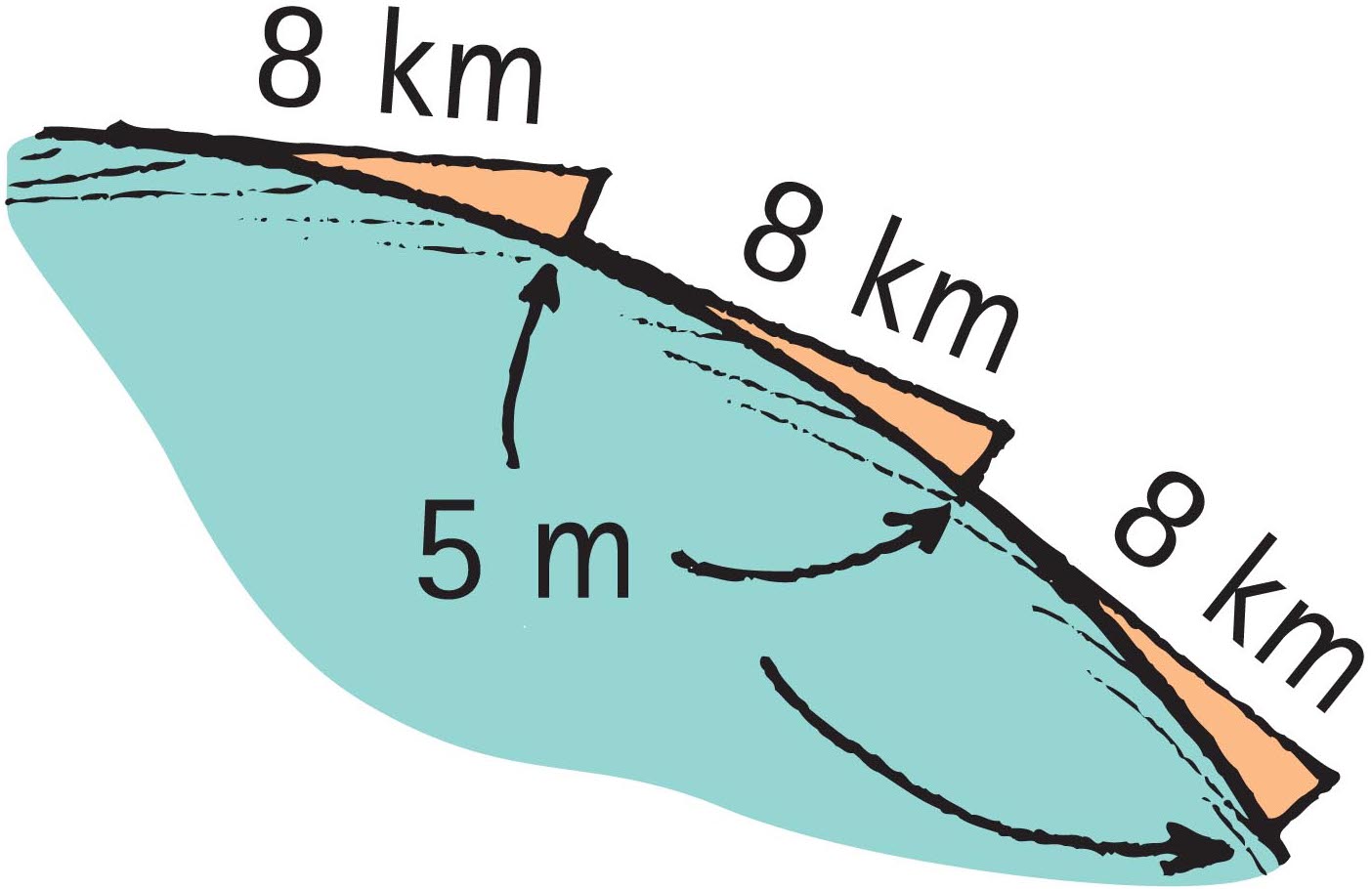
How much tangential velocity must a satellite have to remain in orbit? This question was never answered by Isaac Newton.* With some guidance on your part, your students can calculate the solution. That’s right, calculate the solution without lifting a pen or pencil. First, you assume they’ve learned about projectile motion—that a projectile’s horizontal motion is not affected by its vertical motion. Second, call attention to a geometrical fact: Earth’s surface drops a vertical distance of 5 m for each 8,000 m tangent (Figure 3).

Baseball toss

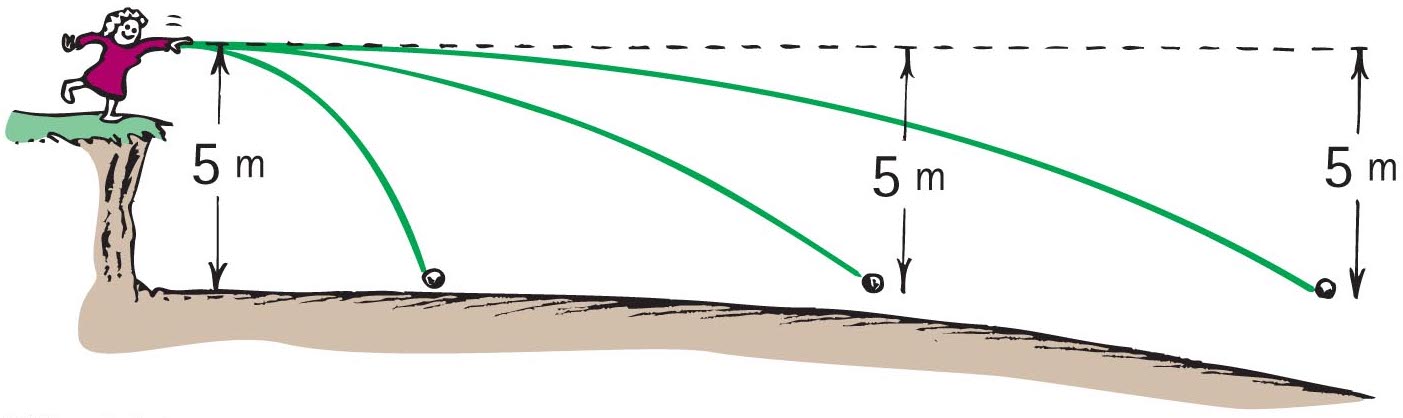
Let’s investigate the 5 m drop of Figure 3 more closely. Consider the horizontal pitch of a ball at a 5 m elevation (Figure 4). Notice that whatever speed imparted to the ball, it will drop a vertical distance of 5 m in its first second of fall. This becomes important when the curvature of Earth’s surface comes into play.

Calculating tangential velocity

Referring to the pitches in Figure 4, ask your students to calculate the pitching speed of a tossed ball that covers a horizontal distance of 8 m in one second. We use this formula: Speed = (distance covered)/(time to fall 5 m). Importantly, the key here is that the time to fall 5 m is 1 second! Guide all students in your class to the answer: Speed = (8 m)/(1 s) = 8 m/s.

When the class is comfortable with that, ask what pitching speed would be needed to cover other similar distances in the same time. After your class seems on board, make this huge jump that refers to Figure 3: Calculate the hypothetical speed if the ball covered 8 km in the time to drop 5 m. Aha! Can your class see the speed would be 8 km/s? Get this: If there were no air drag and no obstructions to motion, the ball would continue making 5 m drops all around the world (Figure 5). It would be an Earth satellite!

Student congratulations

If your presentation is unhurried and your students are in agreement with the 8 km/s answer, congratulate them! They have calculated what Isaac Newton was unable to do more than 300 years ago! They have calculated the minimum speed needed for a satellite to circle Earth. This IS a big aha! Historically speaking, it’s an enormous aha!

Satellite misconceptions

Before leaving this topic, try to correct a widespread misconception held by the general public—that above Earth’s atmosphere is a gravity-free region where artificial satellites orbit. Whoops! Very untrue, for satellites in a gravity-free region would travel in straight-line paths, not the curved ones caused by gravitational attraction to Earth. Gravitational strength follows the inverse-square law, which tells us that the strength of Earth’s gravity in the satellite territory of the International Space Station (ISS) is about 90 percent as strong as at Earth’s surface—not zero.

Do the opposite of Steve’s weak presentation and pronounce with gusto: Satellites that orbit Earth are fully in the grip of Earth’s gravity that causes them to continuously fall around Earth, rather than into it.

Public confusion

Your students have learned what is not generally known: Earth satellites do not occupy a gravity-free zone above Earth’s atmosphere. Public confusion about this may stem from TV coverage of astronauts freely floating inside the ISS. Why they appear to be without gravity, experiencing zero g, is because in free fall they lack a support force, a topic I had the great pleasure of discussing with the first woman to experience outer space.

A conversation with Sally Ride

In 1987, flying home from a meeting of physics teachers, I found myself sitting one seat away from Sally Ride, America’s first female astronaut. How astounding to be sitting so close to this awesome woman! At the time I was revising my high-school textbook and she graciously autographed the page where I discussed satellite motion.

During our conversation she related something that normally isn’t reported in the media—the ordeal that astronauts experience when acclimating to being in space—puking. This occurs due to the absence of a support force. When on the ground, food in our stomach is gravitationally pulled downward. We’re quite acclimated to that. In orbit, there is no up and down. Our stomachs take some time to adjust to what appears to be a zero-g environment.

My meeting with Ms. Ride was at a time when I enjoyed giving guest lectures in elementary and middle schools. A favorite topic with plenty of gems to catch students’ interest was satellite motion. I suggested that by the time they became adults, they may have the opportunity to take an orbital ride in space. Asked for a show of hands, most students indicated they would take such a ride. But when I told my Sally Ride story, with the unfortunate vomiting that went with orbiting, the students changed their minds. Puking is not something kids wish to experience!

* The traditional way to solve for satellite speed in circular orbit is to equate gravitational force F_G to centripetal force F_c. Solving for speed, v = √(GM/r), where G is the universal gravitational constant, M the mass of Earth, and r the radial distance of the satellite from Earth’s center. In Newton’s time, both G and M were unknown, and had to await the experiments of Cavendish in 1798. The present geological method involving Earth’s curvature (Figure 3) awaited this author.

On the web

On www.HewittDrewIt.com are two screencasts for teachers, 148 student-oriented tutorial lessons covering a broad swath of physics, and links to related materials. See also www.ConceptualAcademy.com.

Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, new 13th edition; Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.