Feature
Incorporating Programming, Modeling, and Data Analysis Into an Introductory Biology Course
Journal of College Science Teaching—January/February 2021 (Volume 50, Issue 3)
By Eliot C. Bush, Stephen C. Adolph, Matina C. Donaldson-Matasci, Jae Hur, and Danae Schulz
This paper describes an introductory biology course for undergraduates that heavily incorporates quantitative problem solving in activities and homework assignments. The course is broken up into a series of units, each organized around a motivating biological question or theme. Homework assignments address the theme or question, and typically include a computer programming section as well as a number of written questions. Assessment based on course evaluations suggests that the course was effective in increasing engagement with Biology in a population of STEM-oriented students who are mostly nonmajors.
Over the last several years we have developed an introductory biology course with a strong emphasis on quantitative problem solving. There are several reasons why such an approach is of interest. First among these is the nature of modern biology. Biologists of all types, ranging from wildlife biologists to bench scientists, frequently deal with large volumes of data. It is widely appreciated that this reality needs to be reflected in how we teach (for example, see Vision and Change in Undergraduate Biology Education, AAAS, 2011). While skills such as programming and modeling are most often introduced in mathematics and computer science courses, it is increasingly clear that, given their importance, they should also be included in the biology curriculum itself (Steen et al., 2005; Eaton & Highlander, 2017).
Another broad motivation is the fact that students learn best by doing (Freeman et al., 2014). Work in the laboratory and the field is a classic method for doing biology. However, in today’s world, computational work represents an increasingly common additional method. This raises the possibility of using computation as a medium to help students learn by doing.
Some of our motivations stem from our setting. Our course is taught at Harvey Mudd College (HMC), a small liberal arts college focused on science and engineering. All students at HMC major in one of the STEM disciplines. The course is part of the common technical core, and is taken by all freshmen in their second semester. However, because biology is one of the smaller majors at HMC, the clientele of the course mostly consists of students not intending to major in biology. A chief motivation for the course is to increase the engagement of technically minded nonmajors with biology.
Course description and design
Our goal is to increase student engagement by presenting students with consequential problems from modern biology, and then giving them the tools and biological background to approach those problems.
Structure
We use human health as a unifying theme to bring different topics together in a single semester introductory course, the official title of which is Genes, Genomes and Human Health. We cover topics ranging from evolution and molecular genetics to computational biology. This is broken up into four units: (1) Evolution, Trees, and HIV, (2) Cholera Comparative Genomics, (3) Receptors, Signals, and Immunity, and (4) Disease and Selection in the Human Genome.
Students attend two 50-minute lectures plus a 50-minute recitation (problem-solving session) each week. There is also weekly homework, which typically includes a coding portion (in Python) and a written portion.
A schedule and syllabus for the 2018 course can be found on the website for that offering, which is publically available (Bush 2018a).
Background assumed
The course assumes students have had a one semester introduction to programming in Python (Dodds et al., 2008; Dodds et al., 2010; Dodds et al., 2012). To do the coding homework assignments, they should be comfortable with functions, conditionals and loops, as well as the basic Python data types (strings, lists, dictionaries). A familiarity with recursion is also useful.
Several of the topics make use of concepts from probability and statistics. Thus, having some basic comfort with probability is helpful.
An example unit: Evolution, trees, and HIV
The course is divided into four units. Where possible, these are built around a focal question that provides cohesion and motivation. The first unit of the course begins with the question: Why has HIV/AIDS killed so many people? Over a period of four weeks, we cover concepts and methods that make it possible to approach this question, and students solve related problems on the weekly homework.
Initially, the focus is on mechanisms of evolution. In class we cover the population genetic forces, and on the coding portion of the homework students implement a population genetic simulator. Then for their written homework, students use the simulator they coded to explore how various population genetic processes influence allele frequencies. What they learn can be connected to HIV—for example, that HIV’s large population size inside a patient allows it to efficiently explore the space of possible mutations, and thus evade the immune system. The take-home message of the section is that a grasp of evolution is important for understanding and treating HIV.
In the second half of the HIV unit we discuss the fact that nonhuman primates have a set of related viruses called SIV viruses. Having already introduced phylogenetic trees, we ask what the relationship might be between a primate species tree and the tree for the viruses that infect them. But instead of giving students a phylogenetic tree for HIV/SIV, we have them build one themselves over the course of several homework assignments. The first step is to calculate a set of genetic distances between sequences. In class we derive the Jukes-Cantor model (Jukes & Cantor, 1969). Students then implement this model on the coding homework to calculate genetic distances between sequences (Bush 2018b). The following week, we cover the neighbor-joining algorithm (Saitou & Nei, 1987), and students implement it on the coding portion of the homework (Bush 2018c). Students then use their code and the genetic distances from the previous week to reconstruct a tree for HIV/SIV. Ultimately, they are able to compare this tree with the primate tree and infer that HIV has entered the human population multiple times independently.
The following week, we provide students with a much larger tree containing a number of sequences from group M of HIV 1. They write code to extract the cumulative branch lengths from this tree, and plot them against the collection date for each virus sample. Based on this they can infer that HIV has entered the human population very recently (Bush 2018d). Because new pathogens tend to be more virulent, this connects to our larger question of why AIDS has killed so many people.
One of the features of the unit is homework assignments that build on each other. In the ideal case, to engender a sense of accomplishment and discovery, students would use their own output from the previous week as a starting point for the next week. However, because some students will have problems on one assignment or another, and because we do not want this to interfere with subsequent assignments, we do provide them the input files they need for each assignment.
Highlights from other units
The second unit, Cholera Comparative Genomics, is organized around the question: Why do some strains of Vibrio cause epidemic cholera, while others do not? We take a modern approach to this question, comparing genome sequences from strains that do cause cholera, and strains that do not. In the service of this, students learn about molecular methods such as sequencing and computational methods such as gene finding and alignment. One of the assignments on the homework involves implementing a probabilistic gene finder (Bush 2018e). Students then compare the genes they find in the two strains, and the final assignment offers an opportunity for some discovery. By researching the NCBI annotations for several of the genes that are unique to the pathogenic strain, they can infer something about its transmission. In particular, students can learn that the entire genomic island is part of a prophage embedded in the genome, and that the epidemic-enabling genes (such as cholera toxin) can be transmitted from one Vibrio strain to another by that phage virus (Waldor & Mekalanos, 1996).
The final unit is called Disease and Selection in the Human Genome. It provides an opportunity to see how the concepts and methods we learned about earlier in the course apply to the human genome. One method we discuss is the population genetic measure Fst that measures the amount of genetic variation between populations in a species. On the coding portion of the homework students write functions to calculate Fst given single nucleotide polymorphism data from a set of populations (Bush 2018f). Then, on the written portion, students use this to look for potential cases of positive selection related to alcohol metabolism in humans (Bush 2018g).
From our experience of putting these units together, we conclude that it is possible to use problem solving with quantitative methods as a vehicle for teaching introductory biology. Such methods are another way of “doing” biology, and one which is quite cost effective compared with a traditional laboratory course.
Assessment methods
Assessment of the new course involved comparisons with previous offerings of introductory biology at our institution. In the past the Harvey Mudd core also contained a single semester introduction to biology, organized loosely around the topic of genetics, including Mendelian, molecular, and population genetics. We took two approaches to assess the redesign.
Our first method was to compare course evaluations prior to and following the introduction of the new course. In particular this involved comparing pre-revision course evaluation responses (from 2013 and 2014) with post-revision responses (from 2016–18). This is especially useful for looking at the question of student attitudes toward the course and toward biology as a result of the course.
Our second method was to compare the performance of students on test questions before and after the redesign of the course. We have two test questions that we used on the final exam in the years leading up to and following course redesign. This allowed us to assess how the course redesign affected learning outcomes. The pre-revision data consist of 165 exams sampled from students in the 2014 version of the course. The postrevision data consists of 166 exams randomly sampled from the years 2016–18.
Table 1 shows a comparison of average pre- (2013–14) and post- (2016–18) course redesign evaluation responses. Results from 2015, which was a transition year between the old version and the new version of the course, are also included. Scores are on a seven-point scale (1–7). Post-revision scores are higher for all questions. The p-values for a Wilcoxon test comparing 2013–14 versus 2016–18 were all highly significant (p < 5e-7).
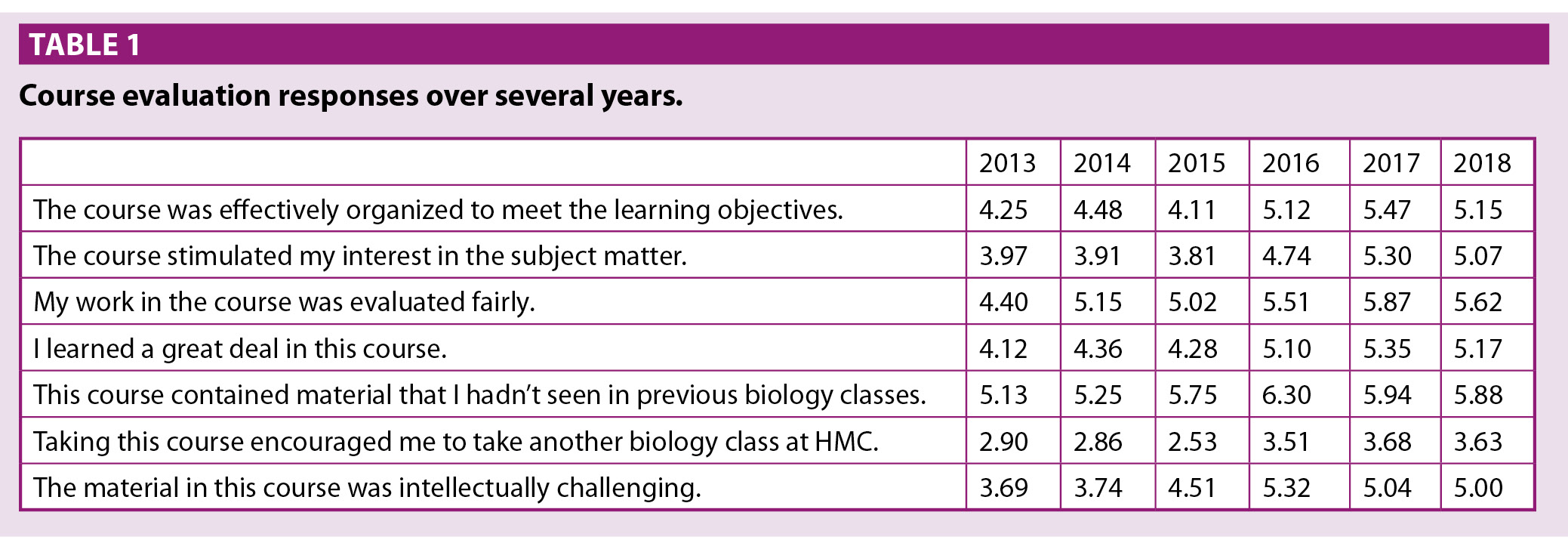
Course evaluation responses over several years.
In developing the course, we had a particular goal of increasing interest and engagement among students. The responses to “The course stimulated my interest in the subject matter” and “I learned a great deal in this course” both increased by about one point, suggesting some success toward our goal. This increased engagement may partially reflect the presence of material that is novel to many students. Responses to the question “This course contained material that I hadn’t seen in previous biology classes” increased by more than a point in the post- versus prerevision periods. It may also relate to the level of difficulty. Scores for “The material in this course was intellectually challenging” also increased substantially. This may be an avenue by which our addition of more quantitative problem solving increased the level of student engagement.
Our final exam-based assessment had two questions. One assessed learning in an area of molecular genetics, focusing on the processes of transcription and translation. The second assessed understanding of molecular evolution, relating to substitution rates at different codon sites. Both of these topics were covered in the course before and after the change. In revising the course to have a more quantitative emphasis, we hoped that students would nevertheless keep learning these topics effectively. The boxplot in Figure 1 shows that student performance pre- and post-revision is nearly identical. This suggests that the increases in engagement and interest we have observed do not entail sacrifices in performance on topics such as these.
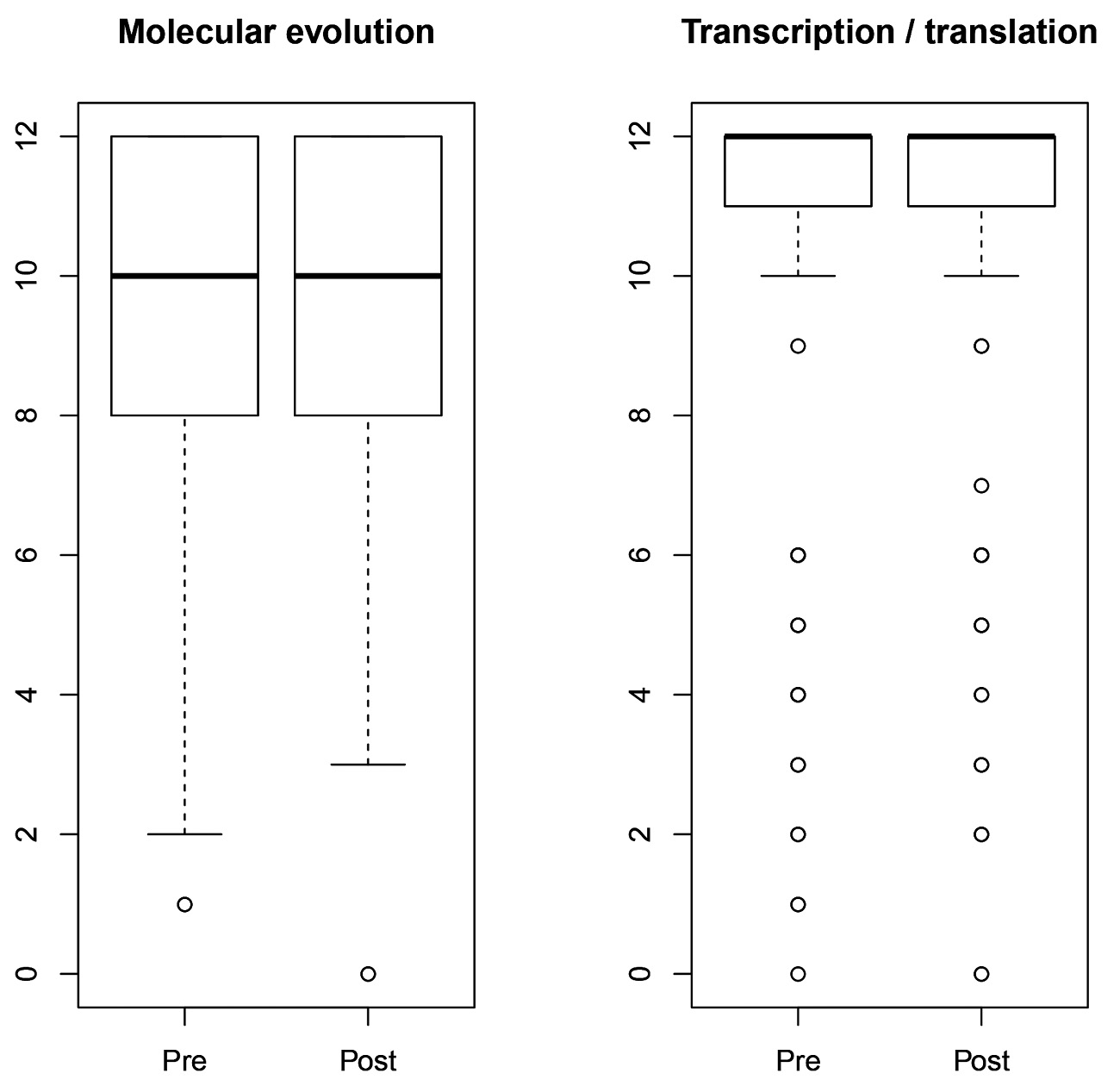
Boxplots showing pre- and postrevision performance on two final exam questions. These questions were graded on a 12-point scale and given on the final exam both before and after the course was revised.
Overall our results suggest that use of programing and quantitative problem solving can be useful in engaging STEM-oriented introductory biology students. While having a population of students with the necessary programming prerequisite is unusual, we think there are other settings where this sort of course might be possible (e.g., in bioengineering programs where a course of this type could be offered as an alternative to more traditional introductory biology class).
The homework assignments and supporting data files for our course are freely available (see Bush 2018a). PowerPoint slides and autograding scripts for the homework are also available upon request. We hope that either our materials, or the spirit of what we have done might be of use to others.
Conclusion
We developed an introductory biology course for undergraduates that makes heavy use of programming, modeling and data analysis. Our assessment efforts suggest this approach was effective in increasing engagement with biology in a population of STEM-oriented students. ■
We would like to thank Laura Palucki Blake, Eric Ditwiler, and Molly Stoykovich for help with the assessment of this course.
Eliot C. Bush (bush@hmc.edu), Stephen C. Adolph, Matina C. Donaldson-Matasci, Jae Hur, and Danae Schulz are all professors in the Department of Biology at Harvey Mudd College in Claremont, California.
Biology Interdisciplinary STEM Teaching Strategies Postsecondary


