Feature
Practice Makes Better
A Classroom Investigation of Practice Effects
Practice effects are ubiquitous human phenomena that have been scientifically studied for over half a century. They are also among the most directly applicable psychological phenomenon, holding broad implications for any domain involving human expertise, and especially for education. Yet the details of how practice works to improve performance are often poorly understood by the users of this phenomenon, such as teachers and coaches. In this paper I describe a simple classroom activity, The Seeker Game, which introduces students to the basics of practice effects, and to some of its complexities. After describing the game I suggest directions for discussion, focusing on “Microgenetic Analysis,” a method that exposes the sources of performance change in detail. This analysis reveals the multifactorial nature of change, demonstrating that performance change often takes place not primarily in participants’ heads, but spanning the cognitive, physical, and social domains.
Practice makes perfect, or at least better. One of the most well-documented phenomena in cognitive psychology is that the speed (or accuracy, or fluency) of an activity improves with practice, that is, as the activity is repeated. This phenomenon, sometimes called the “Practice Effect,” is ubiquitous, and has been scientifically studied for over a half century (Crossman, 1959). It is also among the most important of psychological phenomena, holding broad implications for any domain involving human expertise (e.g., Martin et al., 2011; Côté et al., 2007).
The Seeker Game is a simple activity that introduces students to the most important and interesting aspects of practice effects. The game can be played with almost no preparation, and is easily modified for a wide range of ages and abilities. After describing the game, I suggest directions for discussion, focusing on the “microgenetic” analysis of change—that is, looking in detail at exactly what changes from round to round, leading to the observed practice effects. In these discussions I emphasize how change is multifactorial; that is, it does not take place only, nor even primarily inside the players’ heads, but rather straddles the cognitive, social, and physical domains. I also touch on some topics for more advanced discussion around the game.
The Seeker Game
I use The Seeker Game in my applied cognitive science course at Stanford, after students have been introduced to the basics of applied cognition, especially the concepts of problem-solving and cognitive strategies. However, I have used the game with children as young as seven years old, and one can introduce the relevant cognitive concepts through the activity itself. Below I describe the game in its simplest form. For younger students I add an adventure-style cover story.
Setup: The game requires only cardstock (or manila folders), several sets of stick-on numbers (e.g., 1–10), and a second timer that goes up to a few minutes. Nothing here depends upon high precision. I break up the class into teams of about three students each, distribute a page and sticky numbers to each team, and ask them to each create a random pattern of numbers on their page. The only requirement is that the lowest number must be placed in the upper left-hand corner of the page. The rest of the numbers should be distributed randomly about the page. Figure 1 depicts one such pattern.
Play: Team members distribute the roles of “Seeker,” “Guide,” and “Timer” among themselves. The main phase of the game is played in about six rounds or trials. The goal of the seeker is to touch each of the numbers in order, beginning at 1 and ending at 10. The timer will time how long each round takes. What makes this interesting is this: The seeker must keep their eyes closed the entire time, therefore the guide must help the seeker reach the goal. However, the guide may not touch the seeker or the page, so the seeker and guide must collaborate to get the seeker through the pattern, touching each number in order, using voice direction or some other sort of auditory signal.
In practice, each round works like this: At the beginning of the round, the guide moves the seeker’s hand to the first number, on the upper left of the page. This is the only case where the guide can touch the seeker. When signaled by the timer to start, the guide then guides the seeker to touch each number, in order, as quickly and accurately as possible, interacting only in voice or auditory signals. If the seeker misses a number, the guide must get the seeker to loop back to it so that the numbers are touched in order. When the seeker reaches the last number, the timer records the time for that trial, and the team sets up for the next round. The seeker must not look at the pattern until all rounds are completed.
After ensuring that everyone understands the instructions, I ask all the seekers to close their eyes. At this point I ask the teams to trade their pages around, so that each team now has a new pattern that their seeker has not seen. This minimizes the seeker being helped by a latent memory of the pattern that their own team created.
Recording results: While the teams work, I prepare a graph on the board where the independent (x) axis indicates the round or trial number, and the dependent (y) axis records time in minutes/seconds (Figure 2). Rarely does a trial take more than three minutes. Although there are only five or six rounds in the game, my x axis goes out several additional rounds. These will be used in a transfer phase, described below.
As each team finishes all the rounds, plot their times. Eventually the graph should look something like the left part of Figures 2 and 3.

An example of a Seeker game pattern.
Microgenetic analysis and open discussion
Inviting students to observe the data, the most obvious phenomenon will be that every team overall gets faster, although their paths will, of course, differ, and there are likely to be some points of slowing. The greatest speedup is usually in the early trials, with the speedup decelerating as practice progresses. This is the famous “power law of practice,” although, as discussed later, practice effects may not really fit a power function. I often emphasize this by drawing an “eyeball power curve” through the data (dashed blue curve in Figure 2).
What changes from round to round, leading every team to speed up, and why does the learning take the observed shape? To explore these questions I lead the class in a microgenetic analysis (Siegler, 1987, 1995; Agre & Shrager, 1990) by eliciting detailed descriptions of how each team’s procedure changed from one round to the next.
The first things that will come to mind are cognitive changes in the seeker. For example, the seeker’s memory of the pattern is building up, and they are learning to anticipate where to go next; they are “getting it into their head and hands,” so to speak, a phenomenon sometimes (too simplistically) called “motor memory.” However, it can easily be observed that learning is multifactorial; there are many changes in the strategy employed by the seeker and guide, both individually and as a team. Some of the most obvious changes will be in the communications between seeker and guide. For example, players commonly run into a “left ↔ right” confusion, resulting from the seeker and guide having different points of view, especially if they are sitting across from one another. Most teams facing this sort of problem quickly figure out how to resolve it by using compass points, for example, or more simply moving to a shoulder-to-shoulder arrangement. Another class of common strategic improvements surrounds how the team resolves errors. Importantly, even changes that appear to take place purely in the head (or “hands”) of the seeker rapidly lead to changes in the structure of team collaboration. For example, some seekers learn to use several fingers, or even their whole hand, to find the next number by feel. The discovery of this new sensory facility enables improved efficiency in the guide’s directions. For example, the guide may now only have to give rough direction, being able to lean on the seeker’s new capability.
Open-ended microgenetic analysis, that is, discussion of other changes experienced by the participants, should be encouraged, and occupy a significant period of time. Given space constraints, I cannot go into very many of the changes that will commonly be discovered once the class becomes engaged in microgenetic analysis, but it is worth drawing out the core concepts that should arise:
- Multifactorial change: As previously mentioned, microgenetic analysis will lead to the observation that many things are changing from one trial to the next, including changes in memory, individual actions, communicative acts, and many others. Although the seeker’s memory of the pattern undeniably improves, albeit slowly, many other things change from trial to trial, such as the structure of the collaboration between the seeker and the guide, and the three-way interaction between seeker, guide, and setting, that is, the pattern, how the paper is positioned, what the seeker feels with their fingers, and so on. Early on, the changes in the structure of the team’s strategy generally overwhelm improvements in memory (Haider & Frensch, 2002). Later on, learning is driven by changes that seem more “internal” or cognitive, such as improvements in the seeker’s “motor memory” of the particular path.
- Unpredictability (“contingency”) of learning: At the microgenetic level, each team proceeds along a particular path whose details are due to many kinds of change. There are many, many possible paths to similar end-states. Which particular path a given team takes is highly “contingent,” that is, it depends upon many details of their experience, and of the context, and often of just sheer randomness. As discussed below, teaching, coaching, and parenting are ways that we rein in this sort of unpredictability. Importantly, performance can sometimes slow (become worse). It is interesting to try to understand why this is when it takes place in a given team’s efforts.
- The value and dangers of averaging over individual data to create “laws”: I try to highlight the value of each type of analysis. Average the paths together into “laws” of change can be valuable for prediction, and in design, but such abstractions hide the multiple root causes at the detailed (“microgenetic”) level. Analysis at the microgenetic level is useful in understanding errors, as well as in creating hypotheses about what leads to the overall structure of learning. Both types of analysis have important implications for practice and teaching, some of which are discussed below.
- The limits of learning: There is, of course, a limit to how much one can improve; any action or communicative act takes time, no matter how much you practice, as do cognitive processes. However, in most activities people keep improving, even if in tiny ways, asymptotically heading toward this limit (Crossman, 1959). Although the instructions for the seeker game encourage speed and accuracy, and so explicitly optimize their strategies, people will tend to do so even without instruction (Agre & Shrager, 1990).
- The shape of the average learning curve: Although any setting in which there are diminishing returns will have the sort of sublinear shape approximated by a power function (with a negative exponent), Heathcote et al. (2000) found that an exponential function fits practice effect data better than a power function. However, the observation that many things change from trial to trial suggests the interesting possibility that there are several simultaneous linear functions operating (Côté et al., 2007). The simplest formulation of this hypothesis involves the convolution of two linear functions: a high negative slope “fast” function associated with strategy change, and a less negatively sloped “slow” function, associated with memory improvements. Both of these operate all the way through the task, but early on, strategy change dominates, whereas later on memory phenomena dominate. Sometimes a new discovery at the strategic level can cause a step function later in the task.
Transfer phenomena
An additional phase that I generally add to the basic activity, time allowing, is an exploration of transfer effects. That is, how performance changes when aspects of the task are changed. One could ask the teams to swap the seeker and guide roles, and/or have the teams swap patterns. These manipulations will have a greater or lesser effect of making the activity temporarily more difficult, increasing the rate of mistakes, and the time it takes to complete the task.
I usually do only two or three additional trials with the new configuration, and the right part of Figure 3 depicts actual results in one class. Roughly, the task completion times increase, but not all the way back up to where they were at the start, and rapidly return to their asymptotic march toward the physical limit. This happens because the new task shares much in common with the former task. The advantage deriving from reuse of learnings supported by common elements between tasks is variously called “savings,” “learnings,” or “positive transfer,” and the extra load, and thus lag, resulting from changed, uncommon elements is variously called “loss” or “negative transfer” (Singley & Anderson, 1989).
A typical savings across changes is that the team has already figured out a good communicative strategy, although the particular players might not have practiced these in their new roles. Also, even if the roles are swapped, if the patterns are not swapped between teams, the former guide (who now becomes seeker), will have some memory of the pattern having guided the previous seeker through it several times, although they will not have the “motor memory” that the original seeker had. Notice that if the pattern is changed, the seeker’s memory of the pattern is likely to actually interfere with learning the new one, a source of “loss” (sometimes called “interference”). The more the elements of the task are changed, the more error-prone and slower the activity will become, although learning continues to operate, and performance will continue to improve from the change point forward.
The role of teachers, coaches, parents, and designers
Having observed that strategy change constitutes the greatest part of the practice effect, at least early on, it is natural to ask where strategy changes come from. Unfortunately, like the path contingency observed above, strategy change is also fundamentally contingent. Just as there are many paths to similar endpoints, and which path a person or group takes will depend on tiny details of the participants’ experience and of the learning context, how and when these paths are discovered is fundamentally unpredictable.
People might invent new, efficient strategies on their own, as the teams do in this activity. But in the real world, it is much more common to have strategies culturally communicated: Your piano teacher tells you to hold your hands a particular way, and organizes the pieces you play to build up certain skills; a baseball coach tells you to keep your eye on the ball; your flight instructor tells you to scan your instruments in a particular order; coaches tell us not to practice our mistakes; tutors teach us to use spaced practice; your parents teach you to say “please” and “thank you,” and to look both ways before crossing the street; and so on. Indeed, teaching, coaching, and parenting are all about offering us strategies and guiding us through experiences in an order that will make learning safe and efficient.
Topics for advanced discussion
Here are some ideas for more advanced discussion, given more time or a more advanced course:
- As previously mentioned, Heathcote et al. (2000) found that an exponential function fits the data better than a power function. (For a constant, c, cx is an exponential function, whereas xc is a power function. Additional parameters control the shape and location of the curve.) How could one design experiments to tease apart the power function versus other mathematical forms, and versus more complex models, such as the multilinear model discussed earlier? What statistics would you use to test these hypotheses? Can such an experiment be done without damaging the fundamental interactive nature of the activity?
- What does the universal nature of learning curves tell us about people, either individually or regarding collaboration, and about teaching, coaching, and parenting? How do these practices differ in regard to how they lead students along the learning curve? Is it necessary to pass through a specific series of interim stages in order to reach a desired final strategy? How does this differ for different domains? How does individual discovery interact with “received” (taught) strategies?
- In the seeker game we observe increased speed and accuracy, whereas in other domains, such as musical performance, the goal is not speed so much as accuracy, fluency, and expression. In domains such as mathematics or art, speed apparently does not play any role at all, yet we still see movement toward improvement, whatever the goal. Do similar processes of change underlie all of these? What differs among them?
- How do the structure and interactivity of the team influence learning? Sun et al. (2020) describe a model of collaborative problem solving that has three major subcomponents: (1) Constructing shared knowledge (expressing one’s own ideas and attempt to understand other ideas); (2) Negotiation/coordination—agree upon and execute shared plans of action; (3) Maintaining team function. How do these roles and functions influence practice effects in these sorts of settings?
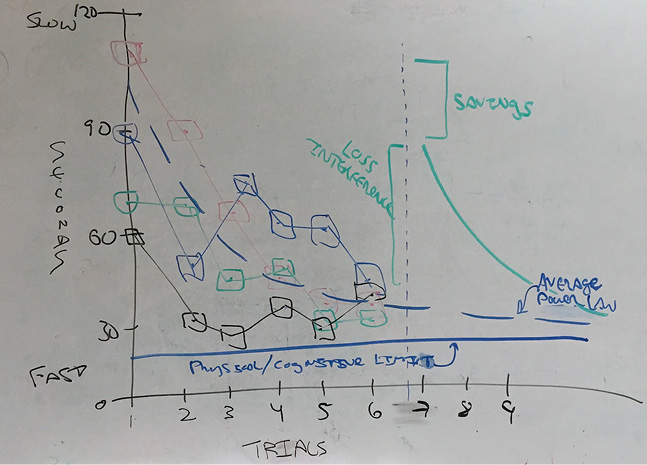
Example results, in addition to the per-team plots. The blue dashed line is an “eyeball average,” and the blue horizontal line at the bottom is an eye-ball asymptotic limit, estimating the fastest possible tour through the numbers.
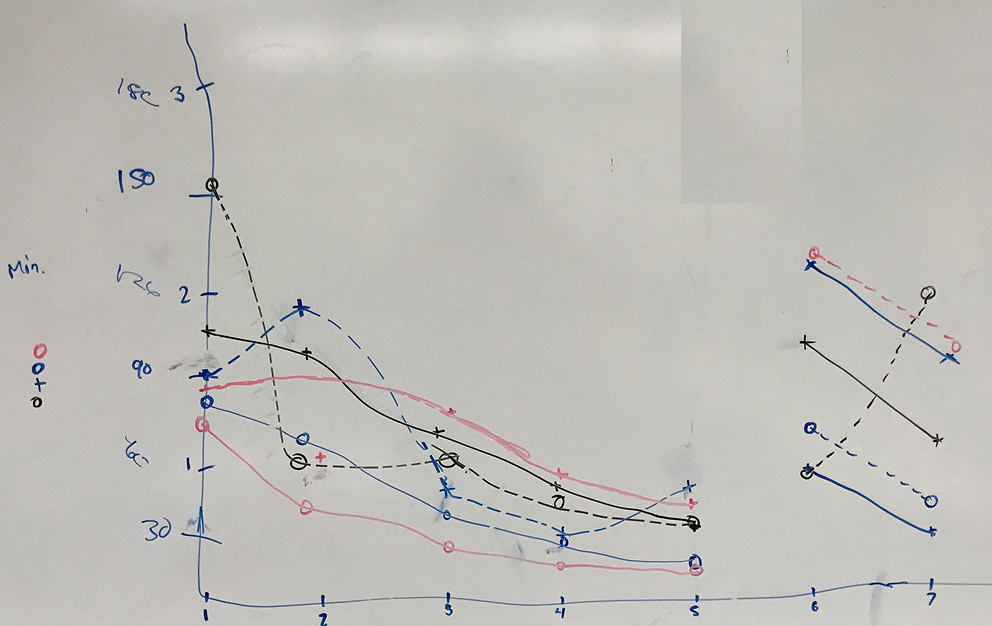
A different in-class run of the experiment. The rightmost two repeats depict savings/loss results after exchange of patterns and roles.
Conclusion and prospectus
Humans are incredible; with only a few simple instructions, even young children are able to succeed and improve in novel, complex activities. We often think of learning in simple terms: “Practice Makes Perfect,” or asserted “laws” such as “The Power Law of Practice.” Microgenetic analysis, looking closely at the sources of change, reveals a complex interaction among the cognitive, physical, and interpersonal elements of human activity. The models that arise from these sorts of analyses have important implications for human performance, as well as in the practical design of educational and coaching interventions, and the engineering of any sort of system that involves people.
The phenomena of practice effects are directly applicable to any domain involving humans. Not only do we communicate strategies to one another through teaching, coaching, and parenting, we design them into our engineered world. Every engineered system embodies a preferred mode of use, and it is expected by the designers that either people can immediately use the device efficiently, or, more commonly, that they can efficiently learn to use it. Indeed, the course that uses this activity is called “Interaction Analysis,” and it is a capstone seminar in the Human-Computer Interaction track within the Symbolic Systems Program—approximately the Cognitive Science department—at Stanford. This course is generally attended by senior and early graduate students in symbolic systems, computer science, psychology, engineering design, and a smattering of students from the “hard” sciences.
Microgenetic analysis of The Seeker Game helps us to see how change straddles the psychological, physical, and social context; when something changes in human activity, the change may be in one person’s head, but most changes involve both individuals and the world, and often involve social connections. The fact that psychological phenomena often occupy a middle-ground between the cognitive, social, and physical domains is one of the aspects that makes psychology a particularly difficult science. Indeed, modern statistics was, in large part, invented to deal with the complexity of psychology. I sometimes joke with my colleagues that the richness and complexity of important human phenomena, such as the practice effect, and the dangers of abstracting “laws” over complex behavioral phenomena, is what makes the “soft” sciences the hard ones! ■
Acknowledgments
I thank the students in my Symbolic Systems 245 course at Stanford, over many years, for their patience and good humor in putting up with playing The Seeker Game, and in helping to improve it. I thank two anonymous reviewers, as well as Dr. Matthew Lewis, and Dr. David Wojnowski for guidance that significantly improved this paper.
Jeff Shrager (jshrager@stanford.edu) is co-founder and director of research at xCures, Inc. in San Francisco, California, and an adjunct professor in the Symbolic Systems Program at Stanford University in Stanford, California.
Biology Phenomena Teaching Strategies Postsecondary


