RESEARCH AND TEACHING
Measuring Computational Thinking Teaching Efficacy Beliefs of Preservice Elementary Teachers
Journal of College Science Teaching—July/August 2020 (Volume 49, Issue 6)
By Erdogan Kaya, Anna Newley, Ezgi Yesilyurt, and Hasan Deniz
With the release of the Next Generation Science Standards (NGSS), assessing K–12 science teachers’ self-efficacy in Computational Thinking (CT) is an important research gap to study. Bandura defines self-efficacy as awareness of the individual’s potential and capabilities to accomplish a goal. Teaching efficacy beliefs is a significant identifier of teachers’ performance and motivation in teaching the specific content successfully; however, K–12 science teachers’ CT teaching efficacy beliefs are rarely discussed. Participating preservice elementary teachers (PSET) were enrolled in an undergraduate elementary science teaching methods course during the spring and summer 2018 semesters in a southwestern state university. We administered a CT teaching efficacy beliefs survey at the beginning and end of the related unit (i.e., the intervention). During the intervention, the PSET followed the CT practices by building educational robots, coding visual block-based programs, and solving puzzles in the video game “Zoombinis.” In this paper, we report the impact of the intervention on teaching efficacy beliefs of PSET. We used SPSS software to analyze our quantitative results. We performed paired samples t-test for the two teaching efficacy beliefs subscales, Personal Computational Thinking Teaching Efficacy (PCTTE) and Computational Thinking Teaching Outcome Expectancy (CTTOE), to measure if there is a significant difference in teaching efficacy beliefs. Our research findings suggest that introducing CT increases PSET CT teaching efficacy beliefs. Furthermore, based on the results of our exploratory research with PSET, we propose implications of the study for K–12 CT teaching efficacy beliefs and CT education research.
It is crucial for the United States to prepare students as early as possible for the jobs that do not exist yet in Science, Technology, Engineering and Math (STEM) and Computer Science (CS) (CSTA, 2013; Google, 2015). While many initiatives have made gains for the STEM pipeline, according to research, the largest industrial growth is in computer science, and yet computer science is still not taught in most schools (Angeli et al., 2016; Blikstein, 2018; Code.org, 2019). Due to the exponential integration of CS into all science fields, there are few if any careers that will not be affected by computing. For example, the fields of neuroinformatics, computational statistics, bioinformatics, mathematics, science, and CS have been seamlessly blending to create new STEM+CS careers (Blikstein, 2018; Code.org, 2019; Sahami et al., 2011).
CS courses require money, infrastructure adaptations, and specialty teachers, however, a more feasible solution that can still meet comparable student outcomes is to integrate computing and coding under the computational thinking (CT) umbrella in science classrooms (Qualls & Sherrell, 2010; Weintrop et al., 2016; Yadav et al., 2016). Integrating CT in elementary is critical to the overall development of STEM+CS literacy in the United States. STEM+CS literacy can be defined as making informed decisions in science and technology-based issues and being engaged in STEM+CS fields (Lu & Fletcher, 2009; Qualls & Sherrell, 2010; Yadav et al., 2011). The Computer Science Teacher Association (CSTA), The International Society for Technology in Education (ISTE) standards, and the Next Generation Science Standards (NGSS) include CT and accept it as an integral part of the curriculum during the elementary grades (CSTA, 2018; ISTE, 2018; NGSS Lead States, 2013). This means that elementary teachers must have the knowledge and skills necessary to integrate CT into their teaching. Preparing preservice elementary teachers (PSET) in developing appropriate pedagogical content knowledge (knowing the ways of how to teach a discipline and knowledge of that discipline) (Shulman, 1986) with regard to CT is a difficult undertaking. It requires professional development to modify current teaching methods and designing high-quality courses to prepare PSET for integrating CT into their teaching (Yadav & Berges, 2019; Yadav et al., 2011).
In the literature, we could not find any research investigating changes in PSET CT teaching efficacy beliefs before or after an intervention within the context of a science teaching methods course. Without the proper training, it can be assumed that elementary teachers lack sufficient confidence to teach CT. However, it has been shown that elementary teachers’ and PSET pedagogical content knowledge and teaching efficacy beliefs can be improved after a well-designed professional development program (Deniz et al., 2018; Jarrett, 1999; Kaya et al., 2019a; Wingfield et al., 2000). The goal of this research is to investigate the changes in PSET CT teaching efficacy beliefs after their exposure to CT activities, including coding with visual block-based programming, integrated engineering with robotics challenges, and playing the Zoombinis video game in an elementary science teaching methods course.
Literature review
It is essential to have early detection of low self-efficacy in teaching because teachers’ self-efficacy beliefs are strongly correlated to their teaching attitudes (Tschannen-Moran et al., 1998). Bandura defines self-efficacy as “beliefs in one’s capabilities to organize and execute the courses of action required to produce given attainment” (Bandura, 1977). There are many research studies that highlight the positive correlation between teaching efficacy beliefs, improved teaching methodologies, and student achievement. On the other hand, teachers with low teaching efficacy beliefs in a certain subject area may neglect or minimize teaching for that subject. For prospective teachers, teaching efficacy beliefs is an important construct that influences their teaching strategies and decisions (Bandura, 1993; Bandura, 1997; Betoret, 2006).
Similarly, science teacher education has many goals, and with the recent adoption of the NGSS, teaching CT is one of them. Based on Bandura’s self-efficacy theory, PSET confidence in their ability to teach CT successfully is an important concern. Without holding high CT teaching efficacy beliefs, PSET may be less likely to teach CT. Therefore, it is important that instructors provide training to improve PSET CT teaching efficacy beliefs and assess the influence of the training on PSET CT teaching efficacy beliefs in science teaching methods courses. To be able to successfully measure PSET CT teaching efficacy beliefs, we employed a modified version of Science Teaching Efficacy Belief Instrument-Preservice (STEBI-B) (Enochs & Riggs, 1990).
Enochs and Riggs (1990) developed the STEBI-B based on Bandura’s theory of social learning. STEBI-B is a 23-item, 5-point Likert type scale (1: Strongly Disagree, 5: Strongly Agree), a valid and reliable instrument, and it contains items such as, “I know the steps necessary to teach science concepts effectively” and “I will typically be able to answer students’ science questions” (Bleicher, 2004; Enochs & Riggs, 1990). STEBI measures two components of teaching efficacy based on Bandura’s self-efficacy theory: personal science teaching efficacy and science teaching outcome expectancy. Personal teaching efficacy is teachers’ beliefs about the effectiveness of their teaching and outcome expectancy is their belief that their teaching will have an influence on students’ understanding. STEBI-B has been modified and successfully administered frequently to assess these two subscales: personal teaching efficacy beliefs and teaching outcome expectancy of PSET in different domains (e.g., engineering, math) without losing its validity and reliability (Yesilyurt et al., 2019a).
There is a substantial amount of research about teachers’ teaching efficacy beliefs (Betoret, 2006; Skaalvik & Skaalvik, 2007; Tschannen-Moran & McMaster, 2009), however, we were able to find only one paper about CT teaching efficacy beliefs (Özçınar & Ozturk, 2018). This paper reported about an instrument designed to measure Turkish preservice computer science teachers’ CT teaching efficacy beliefs. Some theoretical articles inform us that teachers hold naïve views and incomplete knowledge about CT teaching (e.g., Barr & Stephenson, 2011; Yadav et al., 2011). However, research also underscores that, with professional training provided by experts, teachers’ pedagogical content knowledge and teaching efficacy beliefs increase in the content area they teach (Deniz et al., 2017; Jarrett; 1999; Kaya et al., 2019b; Wingfield et al., 2000).
We can benefit from earlier teaching efficacy beliefs research in PSET and in-service elementary teachers. For example, Deniz et al. (2018) organized an engineering professional development in which elementary teachers showed significant improvement in both personal engineering teaching efficacy and engineering teaching outcome expectancy sub-scales after the intervention. Similarly, Kaya et al. (2019b) also found that PSET engineering teaching efficacy beliefs improved as a result of an engineering design intervention including 3-D design and printing. Research indicates that professional development programs that provide firsthand experience in engineering design, information about the NGSS, and sharing best teaching engineering methods and pedagogies have the potential to improve teachers’ engineering teaching efficacy beliefs (Deniz et al., 2018; Kaya et al., 2019b). Because of the improvement described with engineering teaching efficacy beliefs, professional development programs including CT challenges may improve teachers’ level of CT teaching efficacy beliefs. Current teaching efficacy beliefs literature reveals that teachers believe that they can teach the related discipline more effectively when they are equipped with the right materials and have participated in training to improve their teaching efficacy beliefs (Deniz et al., 2017; 2018; Kaya et al., 2019b). In line with this thinking, the goal of our undergraduate level course was to provide opportunities for PSET to improve their CT pedagogical content knowledge and teaching efficacy beliefs in order to transfer and apply CT in their classrooms.
Computational thinking
The term computational thinking (CT) has recently become a common phrase in STEM education. However, among educational stakeholders there is frustration about what it means and its worth in instruction. While it is important to include CT in standards, and the description of the term in CSTA, ISTE, and the NGSS includes CT practices that are fundamental in science classrooms (e.g., data collection and analysis), the descriptions are vague and there is no consensus on CT integration or assessment (Barr & Stephenson, 2011; Weintrop et al., 2016).
Definitions of CT relevant for K–12 education can be summarized as, but not limited to, “solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science” (Wing, 2006, p. 33). The following aspects (see Table 1) have been highlighted during the intervention. These CT principles have been chosen based on their ease of integration into other elementary subjects (e.g., STEM, language arts, history) (Cuny et al., 2010; Newley et al., 2018a, Newley et al., 2019). For example, decomposition can be used in decoding multisyllabic words or completing mathematical word problems. Algorithms and debugging can be applied to the writing process in addition to the applications to science and life skills provided (see Table 1). Abstraction can be used to develop understanding in literature motivations and comparisons between historic and current events. While further examples exist, it is important to note that without training, elementary teachers may not even comprehend the significance of CT or how to develop CT in their students.
| Table 1. Computational thinking aspects related to intervention. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
Introducing CT is essential in K–12 science education due to its power as a significant analytical problem-solving methodology. Integrating CT in K–12 science education requires training all preservice and in-service teachers in CT aspects and instructional practices. Although the lack of consensus about the definition and assessment of CT creates a challenge when planning instruction, it should not prevent any teacher from teaching CT aspects. If we want to address CT in science classrooms, we need to train teachers in CT knowledge with proper instructional methods.
Research question
Recent K–12 STEM education literature emphasizes that exposing teachers to CT as a firsthand experience in professional development or methods courses coupled with reflections can improve teachers computing pedagogical content knowledge (Yadav & Berges, 2019; Yadav et al., 2014). Additionally, studies have found that pedagogical content knowledge correlates with higher teaching efficacy beliefs in that content area (Deniz et al., 2017; Deniz et al., 2018; Jarrett; 1999; Wingfield et al., 2000). Therefore, the goal of our current research is to investigate the following research question:
To what extent will PSET computational thinking teaching efficacy beliefs change after an intervention including the basics of coding, building educational robotics, and playing an educational video game as part of an undergraduate-level science teaching methods course?
Methods
Participants
Our research was designed to examine the CT teaching efficacy beliefs of PSET teachers. Thirty five PSET participants (30 female, five male, ranging in age from 21 to 61 with an average age of 30) were all from a public university of a southwestern state. The PSET took at least two science courses before enrolling in our elementary science teaching methods course as a requirement (minimum = 2 classes, maximum = 4 classes, mean = 2.3 classes), but none of their previous classes included engineering or CT. The participants did not have prior experience in programming, educational robotics, playing Zoombinis, or background knowledge in CT.
Intervention
In our 2018 spring and summer course, we provided modeling, scaffolding, NGSS alignment, and application of CT. This unit aimed to prepare PSET for CT integration in their future science teaching, to increase PSET CT teaching efficacy beliefs, and to improve understanding of CT instruction. The intervention took place twice a week for the last three weeks of a 15-week course (9 hours of a 40-hour total course time). During the unit, the robotics challenges, programming activities, Zoombinis video game, and puzzles allowed PSET to engage in thinking and problem solving. Additionally, the instructors of the course, a science education professor and a computer science educator, explicitly addressed the CT aspects through readings and discussions of the pedagogy of teaching CT in elementary science education (e.g., Yadav et al., 2017). All the resources for the intervention can be accessed by contacting the authors.
Educational robotics
In the first two weeks of the unit, PSET were introduced to the basic components of the Mindstorms EV3 educational robots and they worked in teams to construct their robots by following the building instructions. Then, PSET were introduced to visual block-based programming language, Lego EV3, to command their robots and ultimately accomplish CT tasks. Throughout the robotics sessions, PSET were expected to solve progressively more challenging problems with the theme of space and planet exploration. Using the NGSS engineering design process (EDP) (see Figure 1) and CT aspects in each challenge, PSET were engaged in iterative testing and refinement processes when working on each task. They designed their programs and optimized them to meet the specified criteria. The first challenge taught the PSET basic movements of their robots. In the next robotics challenge, PSET programmed their robots to navigate through a maze autonomously, pick up a box, carry it, and drop the box in a designated square at the end of the maze. While simultaneously working with their team and testing, PSET documented their findings, observations, and reflections in cumulative science notebooks, just as elementary-age students would.
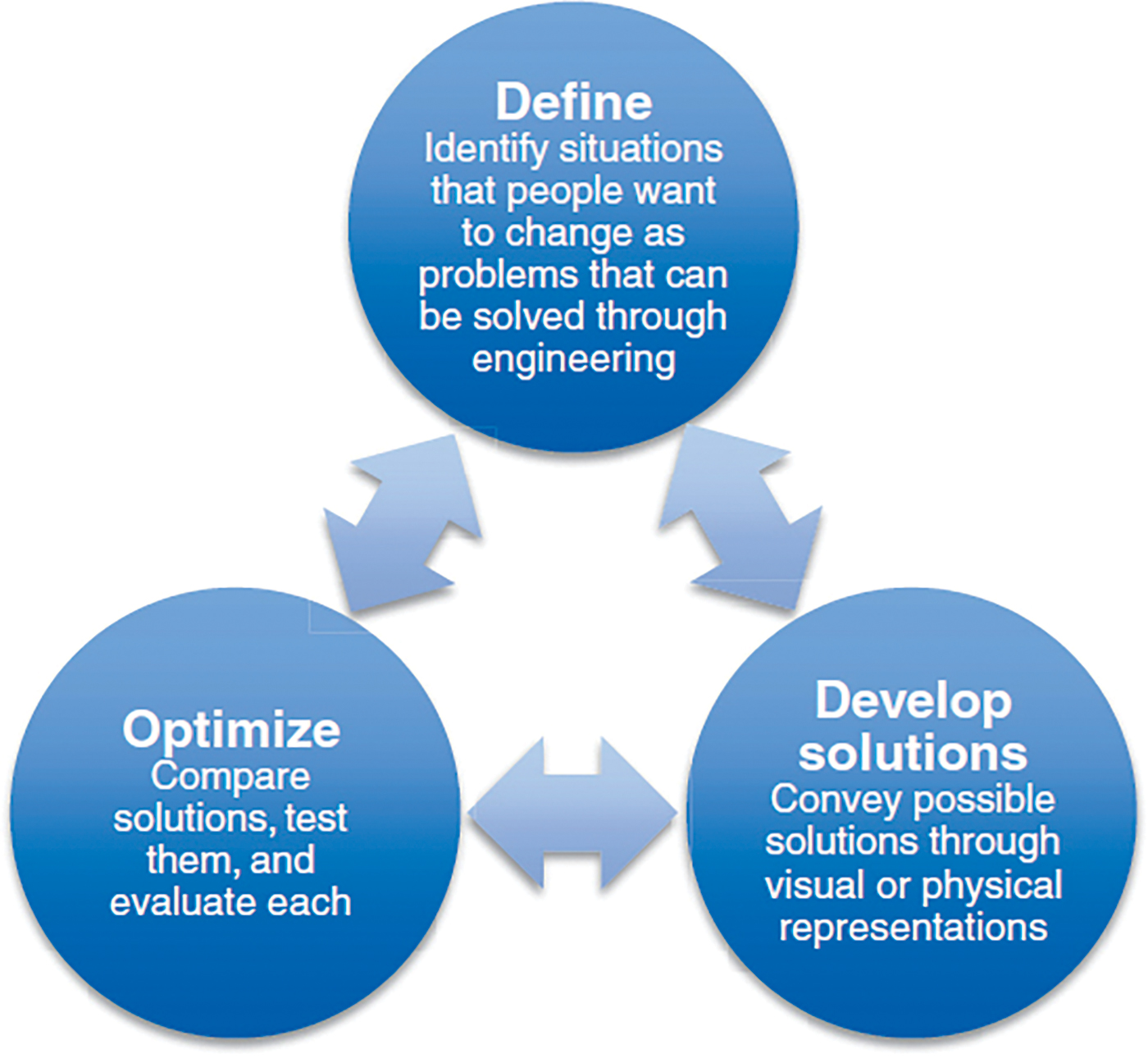
NGSS engineering design process (nextgenscience.org).
Code.org
Throughout the intervention, PSET have applied CT skills through multiple activities (as recommended by Voogt et al., 2015). Following the weeks of robotics, the PSET spent a week building CT skills through a free, browser-based coding curriculum resource: . We applied coding into our CT intervention because this popular method of digital learning provides students with the opportunity to develop and share games and apps with their peers (Brennan & Resnick, 2012) and programming is a great tool to teach CT (Pérez-Marín et al., 2018).
elementary curriculum helps teachers manage student pacing, feedback, and supervision. For students, the drag-and-drop programming and character graphics make the assignments feel like games. When using text-based programming, focusing on syntax errors or technical jargon can be intimidating for novice coders. To help bridge the gap between text-based and block-based coding, curriculum provides users with an option to see their block codes in text. It can encourage students to increase practical skills rather than memorizing coding routine. This site is also an important future resource for PSET because values student privacy, collaboration, educational customization of coded projects, and provides ideas for “unplugged” activities to differentiate learning (Code.org, 2019).
The PSET signed up as elementary students and followed the interactive curriculum. In the next session, we introduced the unplugged activities published in the teacher dashboard. Each PSET team picked a different unplugged activity (e.g., Loops, Algorithms, Functions, Functions with Parameters) and worked in groups to prepare and present the activities to the rest of the class.
Zoombinis
Playing video games can be a natural instrument to instruction (Bruder, 2015; Kafai & Burke, 2016; Smaldone et.al., 2016). Students that can feel so much excitement and joy while playing for hours on PlayStation or Xbox are generally lacking this level of motivation during classroom instruction. While there are some exceptions, most educational games are limited in providing entertainment value. We believe that Logical Journey of the Zoombinis is one of those exceptions. The game provides all the playful elements of entertainment games without losing educational benefits (Newley et al., 2018b).
Zoombinis are spherical blue figures that have distinct eyes, hair, and different colored noses and feet. In the game, Zoombinis’ village is invaded by Ogres, and Zoombinis need to find a new place to live. During their journey, they need to solve different logic challenges until they reach their new town (Hancock & Osterweil, 1996). For example, in the Allergic Cliffs challenge, students need to figure out the bridge’s allergy to solve the puzzle. Any of the Zoombinis’ physical attributes might cause the allergy, such as nose color or hair style. Clues may help, but if students do not follow a systematic approach by using CT, too many mistakes cause the bridges to collapse. In the game, there are 12 different challenges, each challenge needs to be completed three times to advance to the next level, and each level of challenges becomes more complex and requires a different solution strategy. The challenges are a perfect fit to introduce CT in elementary classrooms because it requires finding patterns, debugging, collecting data, and analyzing to be able to systematically solve the challenges. The most unique CT feature of the game is that players are expected to solve the challenges only by observing the clues and finding the patterns, which makes it relevant and aligned with real-life problems.
During the last class of the intervention, the PSET played Zoombinis in groups of two to solve the puzzles. To guide and model CT, PSET completed the Zoombinis worksheet to explain their problem-solving approach to completing the challenges. In our discussion on how to integrate Zoombinis in science classrooms, PSET underscored that Zoombinis can be a great tool for CT, problem solving, EDP, math and science, as well as teaching teamwork and collaboration.
Data collection
To assess the PSET’s pre- and postCT teaching efficacy beliefs, we modified the STEBI-B (Enochs & Riggs, 1990) by replacing “science” with “computational thinking” and relied on the already established validity of the original instrument. PSET were given the adapted Computational Thinking Teaching Efficacy Beliefs Instrument (CTTEBI) (see Table 2). CTTEBI is a 23-question, 5-point Likert-type assessment (1: Strongly Disagree, 2: Disagree, 3: Neither Disagree nor Agree, 4: Agree, 5: Strongly Agree) that measures two subscales of participants’ CT teaching efficacy beliefs. These subscales are: Personal Computational Thinking Teaching Efficacy (PCTTE) beliefs (has 13 items in the instrument), which can be described as teachers’ confidence in introducing CT with knowledge, materials, and methods. The other subscale is Computational Thinking Teaching Outcome Expectancy (CTTOE) beliefs (has 10 items in the instrument), which can be explained as teachers’ belief on how much of teachers’ applied strategies will be effective in increasing achievement in students’ CT knowledge and skills. CTTEBI also includes reversed items to increase validity. We measured PSET CT teaching efficacy beliefs prior to and at the end of our CT unit.
| Table 2. Computational thinking teaching efficacy beliefs instrument items. | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Data analysis
We used SPSS 25 for MAC to analyze our quantitative results. We performed the paired samples t-test for the CTTEBI. We reported the scores for the two subscales of computational thinking teaching efficacy beliefs: PCTTE and CTTOE to measure if there is a significant difference in teaching efficacy beliefs of PSET at the beginning and at the end of the intervention. Cronbach’s alpha values for two subscales were also calculated (see Table 3).
| Table 3. Means, standard deviations, maximum and minimum scores, and subscale reliability. | ||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||
The difference between PSET’s pre- and postPCTTE beliefs (t = -7.036, p < .01) was statistically significant. PSET’s PCTTE beliefs did improve as a result of the intervention but PSET’s CTTOE beliefs (t = -1.228, p =.228) did not significantly change despite that PSET postCTTOE beliefs score was higher than their preCTTOE score. We also calculated effect sizes for PCTTE and CTTOE. Cohen’s d values for PCTTE and CTTOE were 0.95 and 0.22 respectively.
Discussion
Expanding teacher motivation through K–12 STEM+CS education triggered the research toward PSET professional development and teaching efficacy beliefs toward introducing CT. In this research, CT teaching efficacy beliefs of PSET was targeted to be improved in the context of an elementary science teaching methods course. We collected data in a pre- and postfashion by using the CTTEBI. Our analyzed statistical reports revealed that there is a significant increase between pre- and postassessment after PSET are exposed to the aforementioned intervention. Our research findings suggest that introducing CT increases PSET CT teaching efficacy beliefs. This can lead PSET to increase CT instruction in elementary classrooms.
We did address the importance of teaching PSET to improve CT teaching outcome expectancy, however, our PSET did not have an opportunity to introduce CT to their elementary students. As a result, it may have affected nonsignificant positive change in regard to CT teaching outcome expectancy. A larger sample size study coupled with factor analysis to establish the validity of the modified instrument and true significance of the study will continue to be our goal for future work.
Limitations
In our pilot study, we used a modified version of the STEBI-B (Riggs & Enochs, 1990) to investigate PSET computational thinking teaching efficacy beliefs out of necessity because we could not locate any validated quantitative instrument that measures teacher’s computational thinking teaching efficacy beliefs. Additionally, our sample size was too small to carry out appropriate exploratory and confirmatory factor analysis to assess the validity of the modified instrument. Komperda et al. (2018) highlight that when an instrument is modified (i.e., changing its words), it may influence its structural validity and researchers should conduct a rigorous psychometric analysis of the modified instrument. However, due to small sample size in our exploratory research, we did not have a chance to employ any factor analysis. Nevertheless, STEBI was modified for disciplines such as math (Enochs et al., 2000) and engineering (Yesilyurt et al., 2019b). These cited research evaluated the validity of the instrument on a large scale and found similar factor loadings reported by Enochs and Riggs (1990). For these reasons, we relied on the already established validity of the original instrument.
Conclusion
In this study, we reported the findings of our exploratory research with 35 PSET. The overall goal of our research was to train PSET in CT by providing comprehensive CT instruction and sharing resources for their future elementary classrooms. CT teaching efficacy beliefs of teachers is an emerging construct in K–12 science education. This work-in-progress aims to understand PSET teaching efficacy beliefs about CT and could also offer beneficial science teaching methods to higher education instructors who strive to modify their current methods and update their curricula. Measuring and improving PSET CT teaching efficacy beliefs may positively influence their future students and STEM instructional decisions.
These preliminary results suggest that PSET are likely to improve their CT teaching efficacy beliefs after being exposed to CT training. Teachers with higher teaching efficacy beliefs perform better in teaching and learning (Gibson & Dembo, 1984). Professional development opportunities and proper training in teaching methods courses can provide teachers with the opportunity to increase their pedagogical content knowledge and are important ways to improve teachers’ teaching efficacy beliefs (Deniz et al., 2018; Jarrett, 1999; Wingfield et al., 2000).
At this time, our work has great potential to increase the teaching efficacy beliefs of PSET, however, our preliminary research is limited with a small sample size. Despite the small number of participants, anecdotal feedback from the PSET has also encouraged us to continue this work. PSET reported that this unit in CT was engaging and fun, as well as challenging, and could be a perfect fit for elementary classrooms.
Future research
Current studies on CT and computing have not consistently focused on teaching efficacy beliefs. CT teaching efficacy beliefs and pedagogical content knowledge are both essential for teacher professional development and they both need to be emphasized. Possible research ideas for future studies include: the robust validation of the CTTEBI, methodologies that enhances PSET and in-service teachers’ CT teaching efficacy beliefs, correlation between CT pedagogical content knowledge and CT teaching efficacy beliefs, and development of a computer science teaching self-efficacy beliefs instrument for preservice and in-service teachers.
Erdogan Kaya (ekaya3@gmu.edu) is an assistant professor of K–12 computer science education in the Division of Elementary, Literacy, and Secondary Education at George Mason University, in Fairfax, Virginia. Anna Newley is a science teacher at Sonoran Science Academy in Phoenix, Arizona. Ezgi Yesilyurt is an assistant professor in life science education at Weber State University in Ogden, Utah. Hasan Deniz is a professor of science education and director of the Center for Mathematics, Science, and Engineering Education at the University of Nevada Las Vegas in Las Vegas, Nevada.
Assessment Curriculum Postsecondary


