feature
Justice-Centered STEM Education With Multilingual Learners
Computational Modeling to Address COVID-19 Disparities
Pressing societal challenges, such as COVID-19 and climate change, disproportionately impact racial and ethnic minority groups. Traditionally, pressing societal challenges have been left out of science instruction (Lee and Grapin 2022). When science instruction fails to bring pressing societal challenges into the classroom, it fails to affirm and leverage the interests, experiences, and knowledge of minoritized student groups, thus perpetuating injustices in society (National Academies of Sciences, Engineering, and Medicine [NASEM] 2021).
We advocate for justice-centered STEM education that engages students in addressing pressing societal challenges, helps them explain how these challenges disproportionately impact minoritized groups, and guides them to design justice-centered solutions (Lee and Campbell 2020; Lee and Grapin 2022). We focus specifically on justice-centered STEM education with multilingual learners (MLs), a minoritized student group that represents a fast-growing subset of the U.S. K–12 student population. While MLs have been traditionally denied meaningful STEM learning experiences, these students bring a wealth of cultural and linguistic resources that can be harnessed as assets for STEM learning (Grapin et al. 2019, 2021; NASEM 2018).
Given the complexity of explaining and solving pressing societal challenges, justice-centered STEM education calls for leveraging the knowledge and tools of multiple STEM subjects (e.g., science, computer science, engineering). In particular, computational modeling sits at the intersection of computer science and the science and engineering practice of developing models in A Framework for K–12 Science Education (National Research Council 2012) and the Next Generation Science Standards (NGSS Lead States 2013). Computational modeling offers affordances for simulating how the behavior of different agents in a system (e.g., how different people interact in a community) produces the behavior of the system as a whole (e.g., how a virus spreads through a community; Sengupta et al. 2013). Thus, computational models can be powerful tools for explaining the underlying causes of systemic injustices faced by racial and ethnic minority groups and designing systemic solutions that address those underlying causes. Moreover, computational models afford all students, especially MLs, multiple ways to interpret and express ideas (e.g., code blocks, dynamic visualization, graphs; Haas et al. 2021).
In this article, we present a pair of middle school lessons that embodies our approach to justice-centered STEM education with MLs. In these lessons, students engage in computational modeling to explain the disproportionate impact of COVID-19 on racial and ethnic minority groups and then design systemic, justice-centered solutions. As students explain the phenomenon and design solutions to the problem, they use science and engineering practices and crosscutting concepts along with disciplinary core ideas in engineering for middle school (see “Connecting to the Next Generation Science Standards” in Supplemental Materials). To illustrate the lessons, we present examples of student work from Ms. Dudek, who implemented the lessons in her linguistically diverse sixth-grade science classroom in New York City (NYC). We also describe adaptations that Ms. Dudek made to the lessons in her classroom, which offer insights into how the lessons might be enhanced as part of our ongoing design-based research with teachers as co-participants (Barab and Squire 2004). Finally, Ms. Dudek shares tips that can help other teachers bring the lessons into their own classrooms.
Throughout the article, we highlight instructional practices for implementing the lessons with MLs. While valuable to all students, these research-based instructional practices are particularly useful for leveraging the assets and meeting the needs of MLs (NASEM 2018). The complete set of lessons, including the computational models and all accompanying materials (e.g., student handouts), are available as NSTA Daily Do Lessons (see link in Online Resources).
Lesson 1: How are different groups of people impacted when COVID-19 spreads through a community?
In the first lesson, students looked for patterns by racial and ethnic group in COVID-19 data from the Centers for Disease Control and Prevention, or CDC (see Figure 1). The teacher began by orienting students to the rows (i.e., COVID-19 metrics) and columns (i.e., racial and ethnic groups) of the data table. Then, students recorded their noticings and wonderings about the data, which was followed by small-group and whole-class discussions. Small groups consisted of about four students and were intentionally heterogeneous to include both MLs and their peers. During the small-group discussions, the teacher provided examples of how to read a rate ratio: “As of November 2021, Hispanic or Latino persons were 1.6 times more likely than White, non-Hispanic persons to be infected with the virus.” These examples helped all students interpret the data while scaffolding MLs’ use of language for making a comparison (e.g., “ . . . times more likely than”). Overall, students identified patterns related to how racial and ethnic minority groups have been disproportionately impacted by COVID-19.

Sample student noticings and wonderings about CDC data (Lesson 1).
To begin explaining the patterns, students worked with a partner in their group to explore a computational model (developed by our research team). The model represents a community of people at the beginning of a virus outbreak (see Figure 2). This community has implemented a stay-at-home order instructing its residents to stay close to home, to the extent possible (as was the case in many cities at the beginning of the COVID-19 outbreak). At the top of the model, students observed two different shape agents, spheres and pyramids, which represent two different groups of people. Whereas spheres appear as single agents and always stay close to their starting point, pyramids appear in clusters, with one or more of the pyramids traveling out and back from their starting point to random locations (see magnified view of pyramids and spheres in Figure 2). At the bottom of the model, students examined the computer program that tells the agents what to do (see code blocks of different colors snapped together in various arrangements in Figure 2). To guide students’ exploration of the computational model, the teacher projected a series of questions on the board (e.g., “What shapes appear in the model?”; “What patterns do you notice in how the two different shapes are arranged?”; “What patterns do you notice in how the two different shapes move?”).
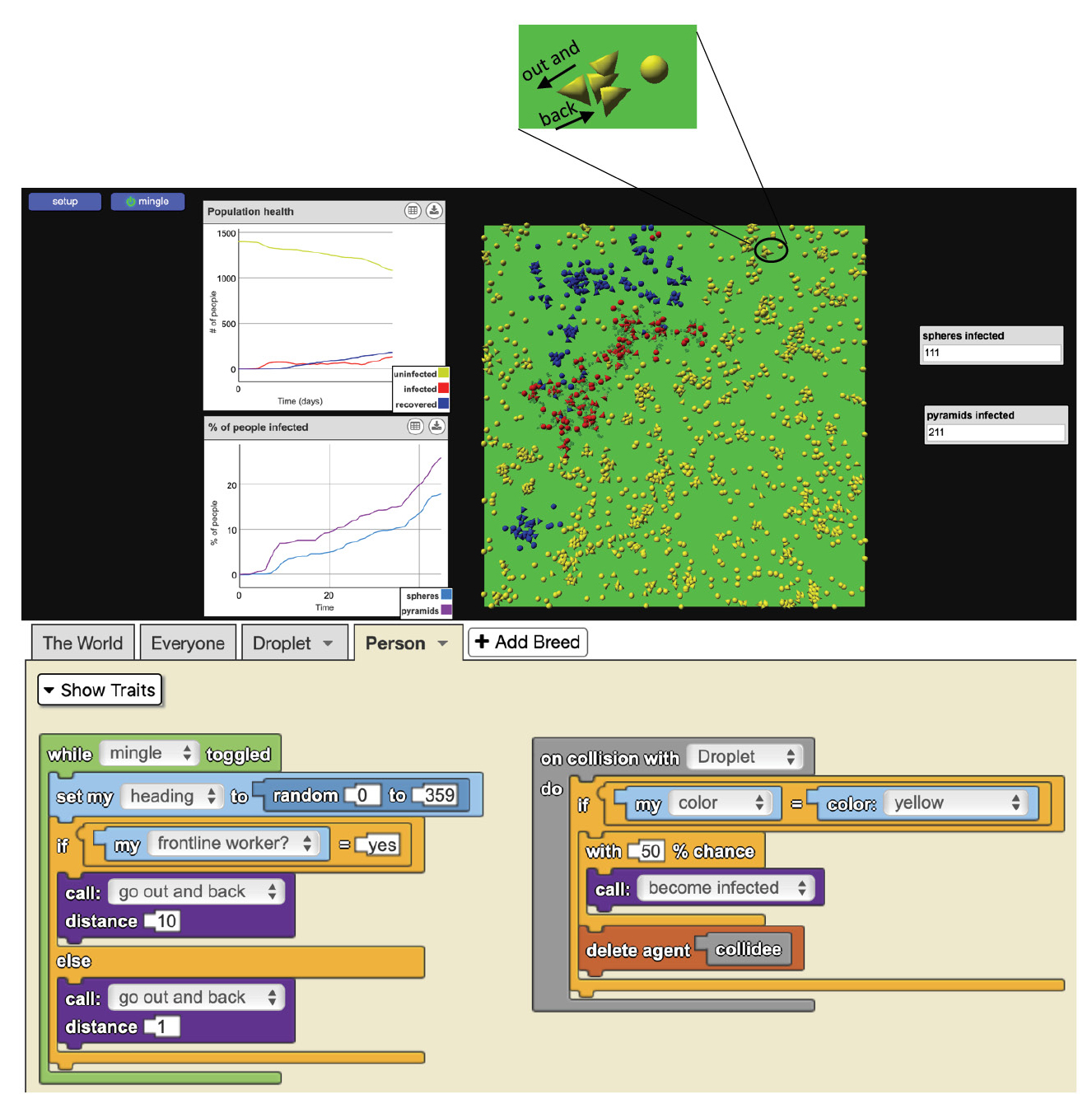
Computational model to explain how different groups of people are impacted by the spread of a virus (Lesson 1). The computational model that appears in this figure is available at https://bit.ly/3YxzrDx
After exploring the model, students made predictions about how the two different agents (spheres and pyramids) would be impacted by the spread of the virus. Then, students tested their predictions by running the model three times and, for each model run, taking a screenshot of the graph that displays the percentage of speres and pyramids infected (see left side of Figure 2).
As students recorded their data, the teacher engaged in formative assessment by listening to partner discourse and asking probing questions to gauge students’ sense-making and push their thinking forward. For example, the teacher asked, “What patterns do you notice across the three graphs?” and “What could the two different shapes represent in the real world?” As students analyzed the data, they identified a key pattern: Pyramids tend to be infected at a higher rate than spheres (see the gap between purple and blue lines in the graph in Figure 2). At the end of this task, students completed an exit ticket in which they summarized their observations and brainstormed reasons why the pyramids moved around more than the spheres. This formative assessment enabled Ms. Dudek to get a sense of the patterns that students were able to identify and what they thought were the reasons for the patterns (see “Sample student response to exit ticket in Lesson 1” in Supplemental Materials). As students related the pyramids to frontline workers in their local community, such as firefighters and grocery store clerks, Ms. Dudek planned to capitalize on students’ local knowledge in subsequent activities.
To explain why pyramids are infected at a higher rate, students interpreted the code underlying the computational model (see bottom of Figure 2). They figured out that while spheres in the model represent households with people who can stay at home (e.g., people who have the option of remote work) and whose living arrangements allow them to maintain distance in their households, pyramids represent households with frontline workers who cannot stay at home and whose living arrangements may prevent them from maintaining distance in their households. Finally, the teacher facilitated a class discussion about limitations of the model (e.g., all agents recover from the virus) and how the model does not include many features of more complex models of COVID-19 developed by scientists.
Throughout Lesson 1, the teacher leveraged the assets and met the needs of MLs. First, the teacher maximized productive talk by having students work in pairs and small groups around data and a computational model. MLs benefit from interactions in which they can use resources in the situation to communicate their observations (e.g., pointing at the model and saying to a partner, “These [i.e., the spheres] don’t move around, but those [i.e., the pyramids] do!”; Haas et al. 2021). Second, the teacher used probes to elicit MLs’ rich knowledge and experiences from their homes and communities (e.g., “In your community, have you noticed that people experience COVID-19 differently?”). These probes, which go beyond general-purpose talk moves typically used with MLs (Grapin et al. 2019), leverage students’ funds of knowledge to enrich their sense-making (González, Moll, and Amanti 2005).
Lesson 2: How can we explain and design solutions to the disproportionate impact of COVID-19 on racial and ethnic minority groups?
The second lesson consists of two parts: (a) explaining the disproportionate impact of COVID-19 on racial and ethnic minority groups and (b) designing solutions to the problem of disproportionate impact.
Explaining the disproportionate impact
This part of the lesson focuses on two conditions that contributed to the disproportionate impact of COVID-19 on racial and ethnic minority groups: (a) frontline work and (b) household living arrangements. The teacher decided to focus on the first condition (frontline work), since the students in her sixth-grade class vividly recalled the stay-at-home order implemented in NYC during spring 2020. It was during this time that the essential services provided by frontline workers became readily apparent to all NYC residents. (To access materials related to the second condition, household living arrangements, readers can visit the NSTA Daily Do Lessons; see link in Online Resources).
Students began by obtaining information and analyzing data from a report about frontline workers in NYC (see link in Online Resources), including who they are, where they live, and how they get to work (see “Tips from Ms. Dudek’s sixth-grade classroom” for further details on how she scaffolded this task for her students). Students figured out that racial and ethnic minorities are disproportionately represented among frontline workers, who often travel long distances to their work where they provide essential services. Students combined evidence from the report with the computational model from Lesson 1 (see Figure 2) to construct written arguments that frontline workers in NYC, who are disproportionately members of racial and ethnic minority groups, are susceptible to COVID-19 infection because of various aspects of their work (e.g., commute on public transportation, lack of health care coverage).
Figure 3 shows an argument developed by one group of students, including the data they used to support their claim. Students were particularly interested in making arguments relevant to their local context in NYC. For example, one student group argued that frontline workers from certain NYC boroughs, such as Brooklyn, might have been particularly susceptible to COVID-19 infection because of the distances they traveled on public transportation to other boroughs, such as Manhattan. Another student group argued that a lack of health care coverage among frontline workers could exacerbate the consequences of COVID-19 infection. This argument, in particular, reflected students’ awareness of the pervasive discourse around universal health care in the NYC political arena, which became a recurring topic of discussion during the lessons. The teacher’s decision to give students agency in determining what claims to make based on the data is a hallmark of differentiation in diverse classrooms (Tomlinson 2014; see “Tips from Ms. Dudek’s classroom” for further details on how she differentiated the argument writing for her students).
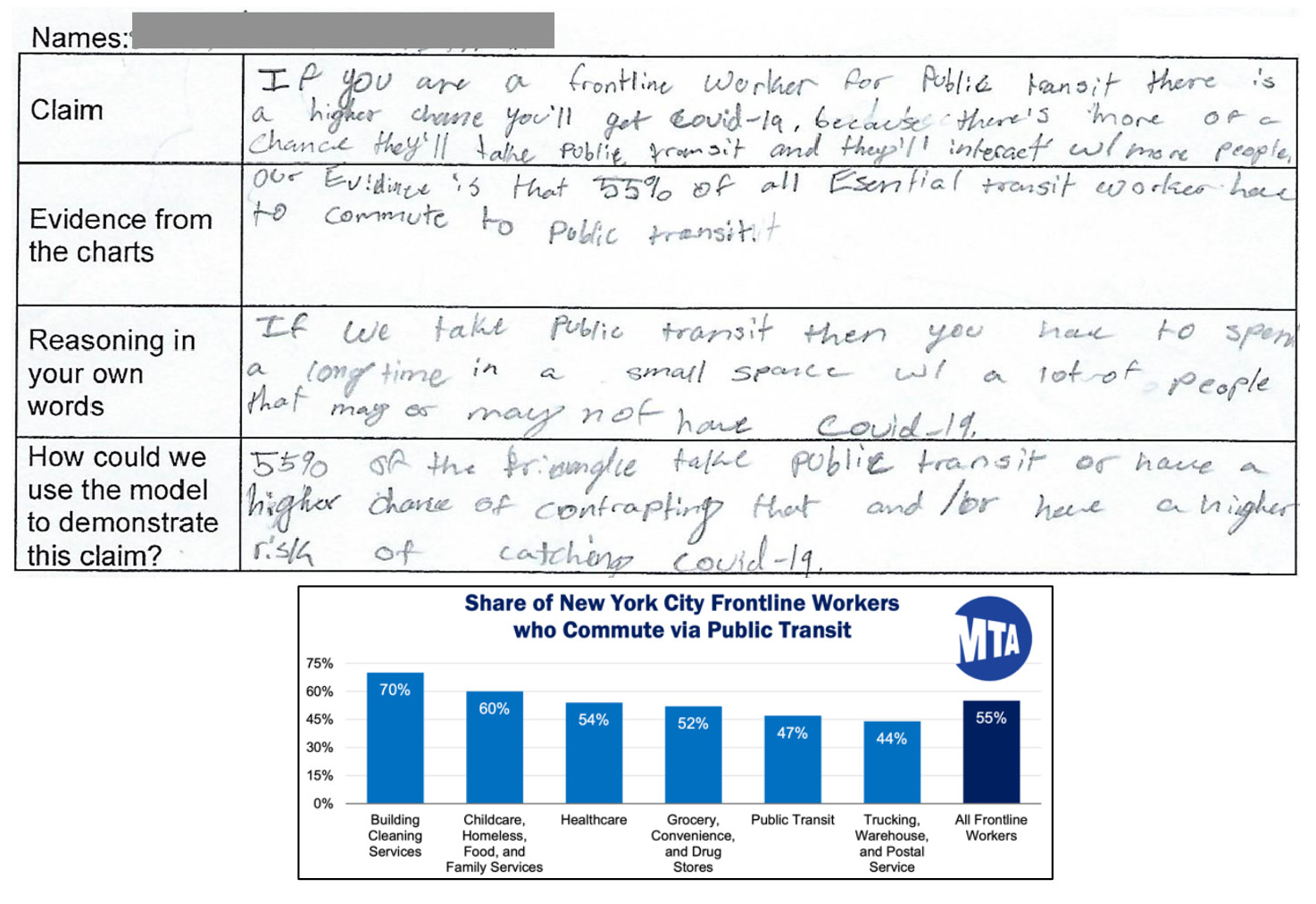
Sample student argument about frontline work (Lesson 2).
Our research team, in consultation with Ms. Dudek, developed a rubric to guide the assessment of students’ arguments (see “Rubric to assess students’ arguments about frontline work” in Supplemental Materials). Ms. Dudek used the rubric to identify areas for improvement in her students’ arguments and provide feedback via conferences with each group. Based on the rubric, key areas for improvement included (a) explicitly addressing the representation of racial and ethnic minority groups in frontline work, (b) strategically combining evidence from the report about frontline workers and the computational model, and (c) coherently organizing different parts of an argument. While future iterations of the lessons will address these areas, students’ arguments illustrate how they leveraged their local knowledge to engage in STEM practices (e.g., computational modeling, analyzing data, arguing from evidence) and to explain a societal challenge that resonated with their lives.
Designing solutions to the disproportionate impact
Having investigated one condition that contributed to the problem of disproportionate impact (i.e., frontline work), students were ready to design solutions. They began by using another computational model (see Figure 4) to test whether mask wearing, a common recommendation for preventing the spread of COVID-19, helps address the disproportionate impact of the virus on different groups of people. In the model, mask wearing is represented on a continuum (see slider for mask effectiveness in the bottom right of Figure 4), since the effectiveness of a mask depends on a variety of factors, including the type of mask (e.g., cloth mask vs. N95 mask), location of contact (e.g., inside vs. outside), and duration of contact (e.g., long vs. short amount of time). As mask effectiveness increases from 0 (not effective) to 3 (very effective), the agents are less likely to be infected by the virus when they come into contact with it.
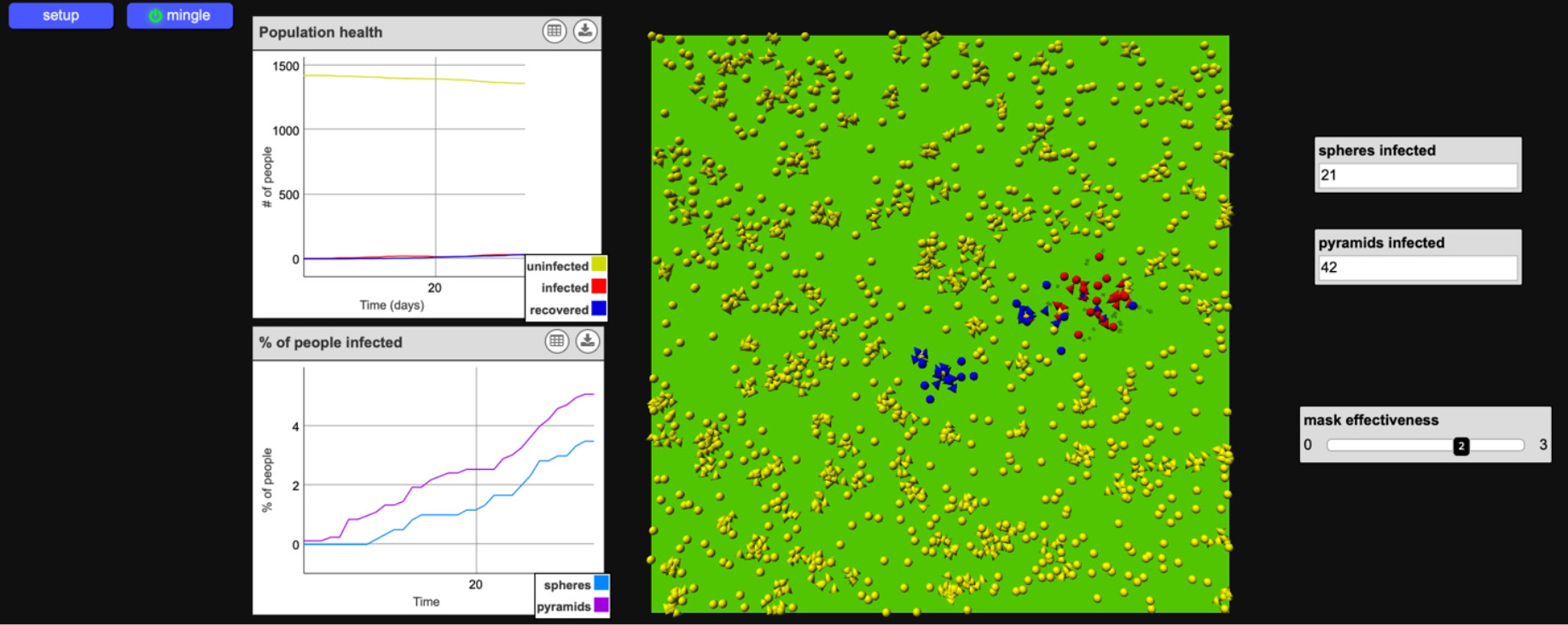
Computational model to test mask wearing as a solution to the problem of disproportionate impact (Lesson 2). The computational model that appears in this figure is available at: https://bit.ly/3JqulVA
As students tested different levels of mask effectiveness, they figured out that while mask wearing results in an overall decrease in infections, there is still a disproportionate impact on the pyramid agents (see persistent gap between purple and blue lines in the graph in Figure 4). Thus, mask wearing is necessary but not sufficient for solving the problem. This is because mask wearing focuses on the behavior of individuals. But the problem of disproportionate impact results from systems that, historically, have failed to meet the needs of certain groups of people. For example, underfunded and inadequate public transit systems have made it difficult for frontline workers to travel safely to work. Systemic problems require systemic solutions.
Students returned to the data sources from earlier in the lesson to identify systemic solutions, such as ensuring safer public transit for frontline workers (from the frontline worker report). These systemic solutions attempt to change systems (e.g., transit systems), which can in turn improve the conditions for individuals.
As a culminating assessment, students worked in their groups to research different systemic solutions from the data sources. Then, each group prepared a PowerPoint presentation for their local city or town council and made arguments for their systemic solution. To support their arguments, groups presented evidence from the computational models and data sources they used throughout the two lessons. While all group members contributed to the conceptualization of their group’s proposed solution, Ms. Dudek differentiated the task by inviting group members to contribute to the presentation in different ways based on their unique interests, experiences, and knowledge (e.g., interest in graphic design, knowledge of data representation). In the Supplemental Materials, we provide a link to a slide from one group’s presentation that proposed several plans of action (e.g., fundraiser, protest) aimed at increasing pay for frontline workers.
As a challenge, groups could also test their systemic solutions using the computational models. For example, they could test whether affordable housing that ensures less crowded living arrangements (represented by smaller clusters of pyramid agents in the model) helps address the disproportionate impact of the virus on different groups of people. Students’ excitement about their proposed solutions was evident from the fact that they continued discussing the merits and trade-offs of different solutions even as they left the classroom and headed to their next class.
Throughout Lesson 2, the teacher leveraged the assets and met the needs of MLs. First, the teacher scaffolded MLs’ argument writing (WIDA 2020) by providing a graphic organizer that included boxes for claim, evidence, reasoning, and connections to the computational model. This graphic organizer makes explicit for MLs the discourse features of a science argument (e.g., evidence is data to support a claim; see “Graphic organizer for argument writing” in Supplemental Materials). Second, for the culminating assessment, the teacher encouraged both MLs and their peers to communicate their systemic solutions using multiple modalities, including graphs, code blocks, and oral/written language. All students, and especially MLs, are able to demonstrate their science learning more fully when they are invited to leverage their full repertoire of meaning-making resources in the science classroom (Grapin et al. 2021).
Tips from Ms. Dudek’s sixth-grade classroom
After implementing the lessons in her sixth-grade science classroom, Ms. Dudek shared the following tips for teachers, which also offer insights into how the lessons might be enhanced:
- As students analyze COVID-19 data at the beginning of Lesson 1, pay close attention to what they notice and wonder. This informal formative assessment will help teachers identify students’ initial ideas about why racial and ethnic disparities exist and then address those ideas productively over the course of instruction. This will also position students’ initial ideas as valuable for sense-making (González, Moll, and Amanti 2005).
- When introducing the computational model in Lesson 1, give students time to explore the model in an open-ended way. This will help orient students to the model (e.g., what agents are included, what happens when different buttons are clicked) and will make the guiding questions that follow more meaningful. This will also give students agency in determining what aspects of the model to focus on (Tomlinson 2014).
- Differentiate the data analysis and argument writing in Lesson 2 for students at your grade level. For example, divide the report about frontline workers into multiple parts and then assign a different part to each student group. After writing an argument based on the data in their group’s part (see Figure 3), students can circulate the classroom and add sticky notes with comments and suggestions to improve the other groups’ arguments (see Figure 5). This way, rather than simplifying the task for MLs, a common practice rooted in a deficit view of these students, teachers can amplify the task (Walqui and Bunch 2019) by having each group analyze a part and then engage in purposeful interactions with their peers. By inviting students to evaluate each other’s arguments, teachers are also engaging students in peer assessment.

Students writing an evidence-based argument and providing feedback on another group’s argument (Lesson 2).
Conclusion
When pressing societal challenges are sidelined in science instruction, minoritized student groups and their communities are sent the message that their interests, experiences, and knowledge are outside the purview of school science. Justice-centered STEM education represents a fundamental shift from centering the knowledge of STEM disciplines (e.g., “follow the science” solutions to COVID-19, such as mask wearing, which overlook minoritized groups) to centering the interests, experiences, and knowledge of groups who have been systemically marginalized in schools and in society. The lessons presented in this article leverage the power of computational modeling to engage middle school students, including MLs, in explaining and designing solutions to the pressing societal challenge of COVID-19, with the ultimate goal of inspiring students to be agents of change toward creating a more just society.
ONLINE RESOURCES
NSTA Daily Do Lessons—https://bit.ly/40bWPYA
Frontline workers in NYC report—https://on.nyc.gov/3TqCZ9Q
Sample student response to exit ticket in Lesson 1—https://bit.ly/40Gd5Se
Graphic organizer for argument writing in Lesson 2—https://bit.ly/3K8QOp8
Rubric to assess students’ arguments about frontline work in Lesson 2—https://bit.ly/3GkybgS
Slide from group presentation advocating for higher pay for frontline workers in Lesson 2—https://bit.ly/3m9HcT0
Connecting to the Next Generation Science Standards—https://bit.ly/3ZKnvPq
Scott E. Grapin (sgrapin@miami.edu) is an assistant professor in the Department of Teaching and Learning at the University of Miami in Coral Gables, Florida; Sharon Dudek is a teacher at Lyndhurst Middle School in Lyndhurst, New Jersey; and Okhee Lee is a professor in the Department of Teaching and Learning at New York University in New York, New York.
Computer Science Engineering English Language Learners Equity STEM Middle School Grades 6-8



