feature
The Fram Polar Expedition and Determining Latitude From Stars
An Earth science student-learning exercise
Before contemporary navigation aids, mariners used astronomical sightings to navigate. This article references the 1893–1896 Fram polar expedition described in the book Farthest North (Nansen 1897). The expedition’s astronomical observations provided the basis for part of a teaching unit on star and constellation identification in high school Earth science classes: a sighting of the star Capella. Basic concepts early navigators used to determine latitude from stars are suitable for students in grades 9–12. This article shares an example of applied astronomy in which students determine latitude from star sightings in a high school astronomy unit.
The Fram polar expedition
The Fram polar expedition was an attempt by the explorer Fridtjof Nansen to reach the geographical North Pole by freezing the ship into the ice and waiting for the Arctic Ocean east–west current to carry the ship toward the pole. During the expedition, there was concern whether supplies would last. With this in mind, the navigator regularly determined the ship’s position from star sightings. However, inclement weather interfered with observations, sometimes for a week or more. During that time, the expedition had no way of knowing its progress. Each day lacking progress to the North Pole consumed more supplies that needed to be used to achieve the objective. Since the ship was locked in sea ice, it couldn’t be resupplied.
The teaching unit
Based on student interest and performance, this star and constellation identification unit was the author’s most successful Earth science unit. The major objective included learning 30 stars and constellations as well as basic concepts and applications involved in that initiative. Students learned concepts through repetitious teaching, including use of astrophotography; a worksheet; and the educational game “Astro-bingo” (Reed 1972). The student worksheet consisted of
- determining star coordinates of selected stars;
- identifying stars from selected coordinates;
- making horizon diagrams to show the relationship between the celestial equator, the North Celestial Pole, star altitudes, and latitude;
- determining the range of circumpolar and rise-and-set stars at a known latitude;
- identifying star magnitudes and other concepts.
The concepts are best described in Naked i Astronomy (Reed 1976).
The student exercise—general information
Ideas and concepts for the exercise are from a National Science Foundation (NSF) course for Earth science teachers. It assumes students can perform simple subtraction and understand a few basic concepts (described in the next section).
Learning tools include a star chart showing star coordinates; a horizon diagram (Figure 1); a 360-degree protractor; and a straight edge, such as a ruler. The author used star charts known as SC1 and SC2 constellation charts. Alternatively, a star atlas or the internet can give star coordinates. However, a star chart shows star and constellation positions relative to others, which is important for star sightings. After students discuss basic concepts, determining latitude from a star sighting takes only minutes to complete.
Horizon diagram.
The referenced star charts were used as a teaching tool in the NSF course and in Naked i Astronomy (Reed 1976), which is a reference that best introduces concepts used in this student exercise. SC1 and SC2 constellation charts are available at Sky.com for $1.65/copy. Enter “SC1 & SC2 constellation charts” into the search function. For a class of 30, that is $49.50 for either star chart. Keep in mind, this student exercise can be done without using star charts since star coordinates are available on the internet. A circular protractor, 3.5 inches in diameter, is also used. These are available from Amazon at $1.77 each. Cost for a class of 30 is $53.10.
Basic concepts
Stars are located using coordinates analogous to latitude and longitude. On Earth, latitude is either above (north of) or below (south of) the equator. In space, declination is equivalent to latitude. A star either has north (positive) or south (negative) declination, depending if it is above (north of) or below (south of) the celestial equator (CE), which is an extension of Earth’s equator out into space. For stars, right ascension is equivalent to longitude. Only declination is considered for this student exercise. The North Celestial Pole (NCP) is an extension of Earth’s North Pole. On Earth, the equator is 90° from the poles. In space, the CE is 90° from the NCP.
The altitude of Polaris, the North Star, above the northern horizon equals your latitude if you are in the Northern Hemisphere. For example, at north latitude 41°, Polaris is 41° above the northern horizon. At the North Pole (north latitude 90°), Polaris is directly overhead (at your zenith). Finally, at the equator (latitude 0°), Polaris is on the northern horizon.
Methodology
The initial step in determining latitude from star sightings is identifying a specific star. Star charts assist in this. For the Northern Hemisphere, Polaris (the North Star) is often the star of choice for this purpose. This is because, as previously stated, the altitude of Polaris above the northern horizon equals your latitude. From this, a navigator can tell the ship’s latitude. However, if clouds obscure Polaris, alternative star identifications are needed. Therefore, early navigators needed to know basic stars and constellations, which was applied astronomy.
After identification, a sextant measures a star’s altitude above the horizon. This information is used in conjunction with an ephemeris (star atlas), a star chart, or an online source that gives star coordinates. This data is plotted on a horizon diagram (Figure 1).
Horizon diagrams
Horizon diagrams (Figures 1–3) are useful tools that illustrate introductory astronomy concepts and applications, including determining latitude from star sightings. These diagrams are semicircles depicting Earth’s horizon and the celestial sphere (sky). Because the Fram polar expedition attempted to reach the North Pole, horizon diagrams in this discussion show the Northern Hemisphere. Such a diagram also includes north and south compass directions, position of an observer (X), and the observer’s zenith (Z) directly overhead. As basic concepts are considered, a horizon diagram will then also include the North Celestial Pole (NCP), the celestial equator (CE), and the location of the sighted star.
Sighting Capella
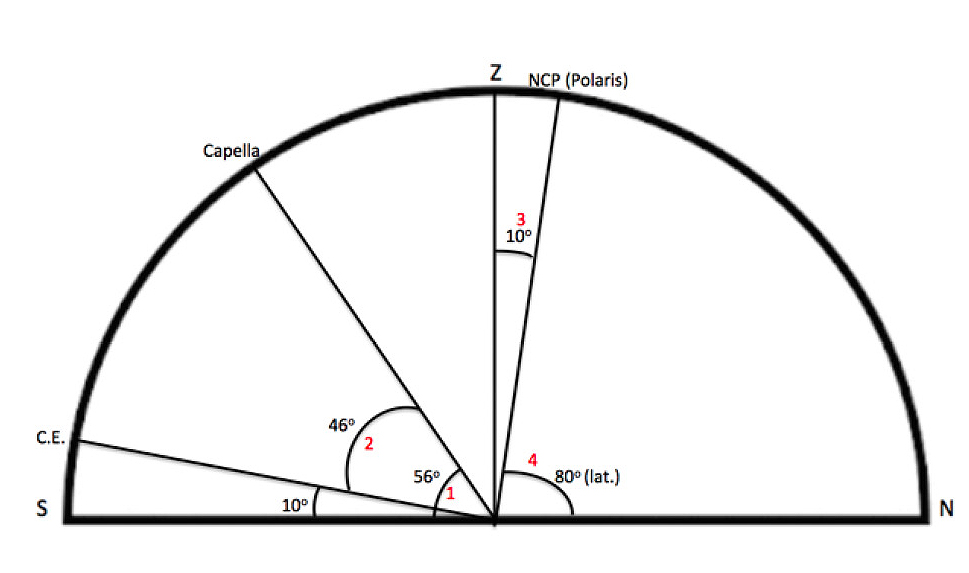
Capella is the alpha (α, brightest) star in the constellation Auriga. Although less familiar than Polaris to most people, its importance to the Fram polar expedition is noted in an entry from the leader’s diary: “An observation of Capella taken in the afternoon [during polar “night”] would seem to show that we are in any case not farther north than 80°11’” (Nansen 1897, p. 214). It was a series of observations like this over days that revealed the expedition’s progress, or lack thereof. Why was Capella sighted and not Polaris? It is assumed clouds blocked the Fram’s view of Polaris. How was latitude determined? Figure 1 shows Capella’s altitude and declination plotted on a horizon diagram. Red numbers (1–4) show steps in determining latitude from this star.
- A sextant shows Capella 56° above the horizon.
- An ephemeris, a star chart, or the internet gives a declination of +46° for the star. By definition, this means Capella is 46° above the CE. Therefore, the altitude of the CE (10°) is known. A question might be: “Above which horizon—north or south—is the CE?” It has to be above the southern horizon because it is always 90° from the NCP. By name, the NCP has to be above the north horizon (Figure 1) in this discussion.
- The position of the NCP (Polaris) above the northern horizon is easily determined because it is 90° from (right angle to) the CE.
- Using a protractor (or plane geometry), the altitude of Polaris is determined to be 80°. From the relationship “the altitude of Polaris above your northern horizon equals your latitude,” the latitude is north 80°.
A quicker solution
It should be obvious there was a quicker solution. Had Polaris been visible, sighting that star would have given the expedition’s latitude. This is because, in the Northern Hemisphere, the altitude of Polaris above your northern horizon equals your latitude. As mentioned, it is assumed clouds obscured Polaris when Capella was sighted.
Other examples
The internet is replete with websites using Polaris to determine latitude. These assume Polaris is visible. They fail to discuss alternative stars a navigator might use should Polaris be obscured. Nautical Almanac lists 58 navigational stars, one of which is Capella. These special stars are among the brightest.
The Capella sighting discussed in this article is from a historical document. Such examples are not readily available for general use. However, based on basic concepts previously discussed, a teacher can make up examples that are equally useful for students. To do so, the altitude above the horizon and declination of a selected star are needed. The former is made up; the latter is from a star chart, an ephemeris, or the internet. Two examples, using horizon diagrams, are shown below. In each example, the altitude of the sighted star is made up. If making actual measurements from the night sky, a sextant would be used.
Example 1
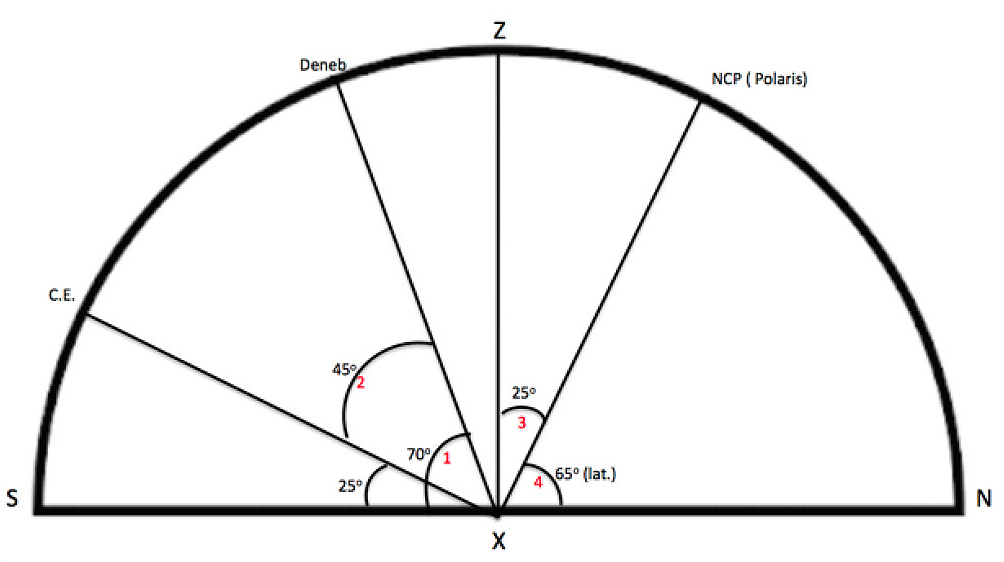
Inclement weather makes sighting Polaris impossible. However, a break in clouds allows a ship’s navigator to sight Deneb (Cygnus) at 70° above the southern horizon. What is the ship’s latitude?
The solution: Look up the declination of Deneb. Steps 1–5 are shown in red on Figure 2.
- On a horizon diagram, show Deneb’s altitude of 70° above the southern horizon.
- Since Deneb has a declination of +45°, the CE is 45° below it.
- The CE is 90° from the NCP (Polaris).
- The altitude of the NCP (Polaris) is determined from simple geometry or from using a protractor.
- Use this rule: “The altitude of Polaris above your northern horizon equals your latitude.”
Answer: 65° N. latitude
Example 2
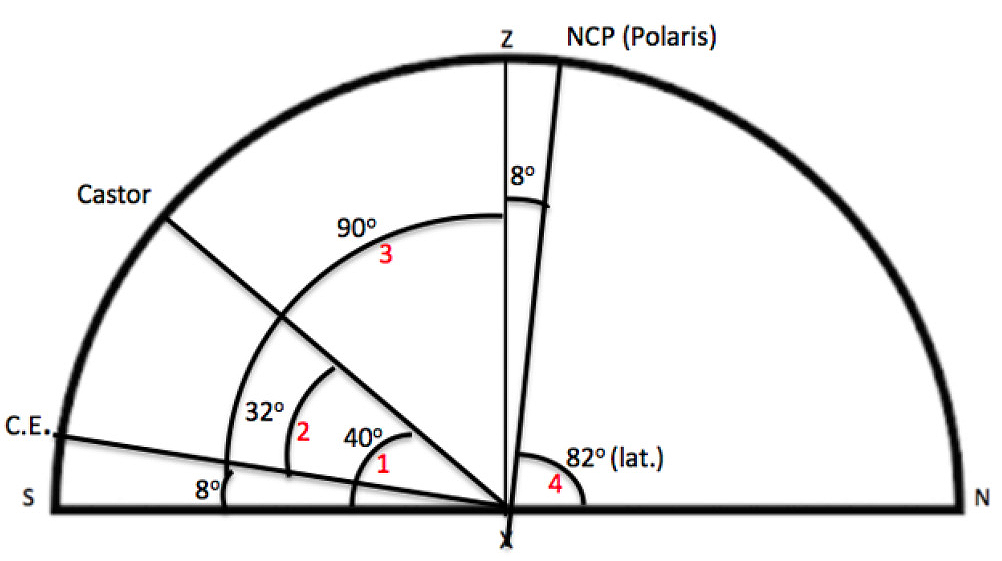
A ship’s navigator sights Castor (Gemini) as being 40° above the southern horizon. What is the ship’s latitude?
The solution: Look up the declination of Castor. Steps 1–5 are shown in red on Figure 3.
- On a horizon diagram, show Castor with an altitude of 40° above the southern horizon.
- Since Castor has a declination of +32°, the CE is 32° below it.
- The CE is 90° from the NCP (Polaris).
- The altitude of the NCP (Polaris) is determined from simple geometry or from using a protractor.
- Use this rule: “The altitude of Polaris above your northern horizon equals your latitude.”
Answer: 82° N. latitude
Conclusion
The Fram polar expedition was successful in that the ship’s innovative design withstood rigors of sea ice and the expedition made scientific observations. At the same time, it was unsuccessful in reaching the North Pole. Star sightings showed ocean currents were not sufficiently advancing the Fram northward. After 18 months aboard ship, the expedition leader and a companion set off on dog sleds, hoping to achieve the goal. They failed in their attempt but advanced to a farthest-north latitude of 86°. Eventually, they reached safety and much acclaim; the Fram drifted into the Atlantic Ocean, intact.
Determining latitude from star sightings puts students nearly on par with early navigators. Star sightings to determine latitude were crucial to the expedition. They are an example of applied, practical astronomy.
Charles Miller Jr. (ch.triassic@gmail.com) is a retired geologist and teacher, State College, PA.
Astronomy Earth & Space Science Instructional Materials Interdisciplinary High School



