Some very worthwhile physics can be taught with just a pair of metersticks and a blob of modeling clay. Here I’ll suggest a few intriguing activities using these materials. We begin with a review of Newton’s second law and free fall.

Free fall

Hold a meterstick horizontally above your head and tell your students that you’re going to drop it. But to make the drop more interesting, compare it to the drop of a glob of clay. Ask which will hit the floor first when both are dropped at the same time. You drop them, and sure enough, your students will see them hitting the floor simultaneously. This is no surprise.

Free fall explained

From an initial rest position, dropping distance is related to dropping time by the equation y = ½ at². Display this equation and point out that since the stick and the clay fall the same vertical distance y in the same time t, acceleration a must be the same too. Then display Newton’s second law equation for acceleration, a = F/m, and ask if the mass of the meterstick or the glob of clay affects acceleration a. The answer is no, for a = F/m = mg/m = g; mass m makes no difference. This simple demonstration highlights some powerful physics, as discovered by Galileo in his famous (although possibly apocryphal) experiment at the Leaning Tower of Pisa more than three centuries ago, and was used to get humans to and from the Moon back in 1969.

Reflex time

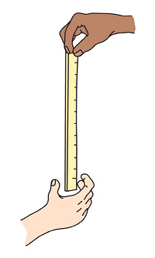
A key feature in most sports is reflex time—the time between hearing or seeing something and reacting to it. Have a student drop a dollar bill between a classmate’s fingers (Figure 2). Even with wide-open eyes and focused attention, can the bill be caught as it drops? With rare exceptions, the answer is no. (Some students may be sure they can catch it, so perhaps let a couple of others try it as well.)

Here’s why the bill is unlikely to be caught: From y = ½ gt², the bill will fall a distance of 15.5 cm (the length of the bill) in a time of about ¹⁄6 second. A common visual reaction time is a little longer, about ¹⁄4 second. That’s the time required for the necessary impulses to travel from the eye to the brain to the fingers. For most people, visual reaction time is longer than the dropping time. Except for a lucky accidental catch, the bill is not caught. This personal and valued activity can be one of many Aha! moments with your students.  Perhaps suggest that they try this activity at home with family members. The result is likely to be a surprise to most people, including adults. It’s nice when students can show off their new knowledge.

Measuring reflex time

Follow up the dropped-bill activity with measurement. After you ask for a few student volunteers, drop a vertically-aligned ruler or meterstick instead of the paper bill (Figure 3). A measure of the distance y of the ruler when caught lends itself to solving for time t, again, with the equation y = ½ gt². When rearranged, it’s t = √(2y/g) = 0.045√y, where y is the distance of fall in centimeters. Comparing one’s value of t with the common ¹⁄4-second reaction time produces yet another Aha! moment. How many students would consider this personal activity irrelevant?

A quick review of free fall is in order before moving on to new material. You’ll want your students to know, and be able to explain, why the weight of the measuring stick has no effect on its rate of fall. As with the meterstick–clay drop, it’s important to know that the weight mg divided by mass m, produces the same acceleration because mass m cancels. Cheers to Newton’s second law! Although repetition can be a teaching no-no, it’s a good thing for cases where central knowledge is being learned.

Center of Mass

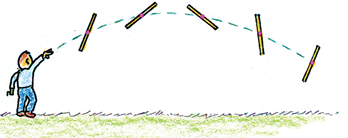
Toss a meterstick haphazardly at an upward angle into the air. Its path is not smooth and it seems to wobble all over the place. In fact, it wobbles about a very special place, a point called the center of mass (CM), which moves as if all the stick’s mass were concentrated there. It is the CM of a thrown object that follows a smooth parabolic path (Figure 4).

Balance

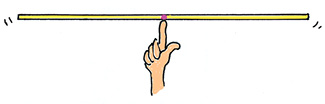
The CM of a meterstick, not surprisingly, is at its geometric center, at the 50-cm mark. That’s why a horizontally-held meterstick will nicely balance when supported by your finger at the 50-cm mark (Figure 5) as you can demonstrate. The CM is a property of the stick, and remains fixed no matter how the rigid stick is oriented.

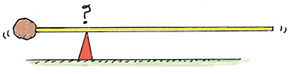
Now consider a pair of metersticks attached end-to-end, perhaps with a piece of tape. One stick is horizontal and the other dangles vertically from the 0-cm mark of the horizontal stick (Figure 6). The sticks are at right angles to each other. Where on the horizontal stick should you place your finger for balance? This is a good time for students to check with their neighbor. After students offer suggestions, have one student try them out. The student will find that the 25-cm mark is the correct place.

Clay–stick balance

To better understand the CM of the two-stick combination of Figure 6, consider a single horizontal stick with a glob of clay stuck at its 0-cm end (Figure 7). For simplicity, the glob has the same mass as the meterstick. (Weigh some clay ahead of time if you want to demo this.)

Questions: Where is the CM of the system consisting of the meterstick and the equal-mass glob of clay? Stated differently, where along the meterstick should the fulcrum be placed for horizontal balance? Can your students see that Figures 6 and 7 employ the same physics?

Vectors

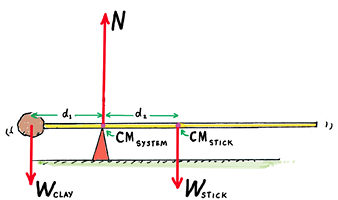
In Figure 8 we show force vectors to add clarity to Figure 7. Downward vectors are shown for the weights of W_clay and W_stick. For the meterstick in equilibrium, the upward normal force N is equal to the magnitude of W_clay + W_stick. The meterstick is also in rotational equilibrium, which tells us that the torque (W × d) produced by the clay’s weight on the left side of the fulcrum is equal and opposite to the torque produced by the weight of the meterstick on the other side. Distances d₁ and d₂ will be equal when both the clay and meterstick have equal weights, as indicated in the figure. You can see there are two centers of mass to consider here: one of the lone meterstick, CM_stick, and the other of the system of meterstick and clay, CM_system. Note that the CM_system occurs at the point of balance, where vector N acts.

Rotational Inertia

Balancing a vertical meterstick on the palm of your hand requires some skill. It is interesting to compare balancing a lone stick and one with a glob of clay at its top end (Figure 9). Experience soon shows that the clay-topped stick is considerably easier to balance. Why this is so involves the property called rotational inertia.

Inertia is the property of a body to resist change. Rotational inertia is the property of a body to resist changes in rotation. The rotational inertia of a vertical stick, or of any rigid object, depends on the axis about which it rotates. The farther the bulk of an object’s mass is from the axis of rotation, the greater is its rotational inertia. So we see that a clay-topped stick on your hand is easier to balance than an empty stick. Circus acrobats who balance a long vertical pole have an easier task when their friends are at the top of the pole. A pole empty at the top has less rotational inertia and is more difficult to balance.

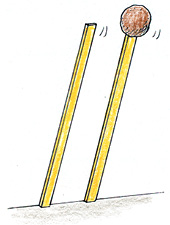
Formulas for rotational inertias of various shapes rotating about certain axes are illustrative. We’ll skip the formulas here because they’re more meaningful if treated after student intuition is nurtured. We’ll instead ask the question posed by Figure 10. When a pair of nearly vertical metersticks are placed against a wall and allowed to rotate to the floor, they’ll do so in the same amount of time. But what if one stick has a glob of clay at its upper end? Which rotates more quickly to the floor?

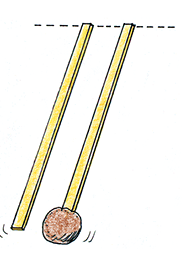
Here we see rotational inertia in action. The clay-topped stick has the greater resistance to a change in motion and lags behind the empty stick that more quickly rotates to the floor. The stick with the clay clearly has more rotational inertia.

Torque

A complete explanation of Figure 10 involves torque. Although greater torque acts on the clay-topped stick than the empty stick, its effect is offset by the greater rotational inertia of the clay-topped stick. Interestingly, if the clay were located at the middle of the stick, the effects of greater torque and greater rotational inertia would balance each other and both sticks would rotate to the floor together.

Pendulum motion

Suspend the two vertical sticks, one with clay, from their ends and you have a pair of pendulums (Figure 11). If they are allowed to swing freely to and fro, is it a challenge to predict which will swing more frequently—that is, with the higher frequency? Won’t the stick with the greater rotational inertia be lazier in its to and fro motion? Which is to say, won’t the empty meterstick swing with greater frequency? Intuition says yes, and watching their swinging motion verifies good intuition. Observing one situation helps to develop intuition to understand other situations.

Stick and slide

My nephew Travis Hewitt rests a horizontal meterstick on his two fingers (Figure 12). As he slowly brings his fingers together, one finger will get a bit closer to the center than the other, where it will press with a bit more force on the meterstick and momentarily stick. Then the opposite finger will slide—until the situation is reversed. The process alternates, a “stick and slide” sequence that always concludes—guess where? That’s right. At the middle of the stick, at its CM. This is true no matter where you initially place your fingers. Demonstrate this, and then let a couple of students try it. Then help the class explain why it operates as it does.

Common sense with structure

How nice that so much physics can be taught with the intriguing behavior of metersticks and globs of clay. The demos are not too shallow, and not too deep—just a good balance to provoke and maintain class interest. With few formulas and no “plug and chug” number crunching, the focus is on student intuition. Let’s not exclude that from our teaching. Physics, after all, is common sense with structure.

On the Web

See complementary student tutorial screencasts 35, 39, 40 and 41 on www.HewittDrewIt.com, and on www.ConceptualAcademy.com.

Paul G. Hewitt (pghewitt@aol.com) is the author of the new fifty-year celebration 13th edition of Conceptual Physics; the 6th edition of Conceptual Physical Science, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.