feature
How Are They Connected?
Teaching electric circuits and Nature of Scientific Knowledge aspects to 11th-grade students using a black-box activity
The Science Teacher—May/June 2022 (Volume 89, Issue 5)
By Anna Koumara, Katerina Plakitsi, and Norman Lederman

For questions like “How is the interior of the Earth structured?” the scientific answers do not come from direct observations. How do scientists make inferences for something they cannot directly observe? The Black Box approach seems ideal to help students understand how scientists work.
Black Boxes are sealed units; their interior is not accessible. The effort to determine their possible content (internal structure) demands successive modifications in hypothesis, measurements, and observations, without opening the Box. There can be more than one suggested inference for its internal structure, compatible with all observations.
One of the first Black Box applications in science education was from Wray (1974), in which first-year university students were asked to specify the connections of electric circuits—this is a creative activity for demanding problem-solving in physics. Similar applications are presented in the works of Terry (1995); Kao, Cina, and Gimm (2006); Rode and Friege (2017) and Harrison (2018). Also, Black Boxes have been used in the experimental part of Physics Olympiads (Chakrabarti et al. 2013).
In recent years, there has been a growing trend to use Black Boxes to teach Nature of Scientific Knowledge aspects through inquiry-based activities (Lederman and Abd-El-Khalick 1998; Aydin and Hanuscin 2011; Miller 2014; Briggs 2019).
This lesson asks students to identify Nature of Scientific Knowledge aspects using a Black Box problem-based activity on electric circuits, and was part of a greater project on the Nature of Science in an 11th-grade science class in Greece.
The Nature of Scientific Knowledge
For the past 100 years, the definition of Nature of Science (NOS) and its aspects have been a matter of constant debate between philosophers/historians/sociologists of science and educators. There is no consensus among them, but they all agree that NOS is a necessary component of science teaching (Lederman, Antink, and Bartos 2014; Piliouras and Plakitsi 2015). Here we prefer to use the term Nature of Scientific Knowledge (NOSK) to refer to the characteristics of scientific knowledge that are inherently derived from scientific inquiry and that are suitable for K–12 students to learn about. Those characteristics are defined below.
Scientific knowledge is empirical; observations and inferences are different
Scientific knowledge is based on/derived from empirical data. Observations are descriptions of natural phenomena that are directly accessible to the senses, or expansion of them. They are subject to limitations of existing equipment and dominant theories, but observers usually reach consensus on what they see/hear/feel, etc. Inferences are the explanation of observations and the same observations could lead to different inferences, according to researchers’ background.
Scientific knowledge is creative
Scientific research, contrary to common belief, is not a rational and orderly procedure. It requires scientists’ creativity and imagination in all parts of research: design, data collection, and invention of explanations, similar to the creation of an artistic work.
Even though objectivity is the goal, subjectivity is unavoidable
Each individual scientist is affected—during interpretation of results, observations, and research design—by his/her personal commitments, previous knowledge, training, expectations, etc. Although throughout history of science, objectivity has been the goal (through standard scales and precision in measurement), subjectivity is present. Also, science is a social activity; scientists interact with each other through scientific publications. Their consequent criticism and continuous testing enhances its objectivity.
Scientific knowledge is durable, but subject to change in light of new evidence
Scientific knowledge is reliable and durable, however, it is not absolute and certain. There is always the chance to alter, either due to evolution in technology and new instruments that lead to new evidence, or because old evidence is reinterpreted.
Science’s sociocultural attributes
Science is a human endeavor that affects and is affected by all societal, cultural, philosophical, religious, political, and economic factors.
Scientific laws and theories are different kinds of knowledge
Laws are generalized descriptions of relationships among observable phenomena and are based on many observations. They describe what happens in the (usually idealized) natural world, but never explain why. Those inferred explanations are given by theories (Lederman et al. 2014).
Survey Sample
The Black Box described below is a NOSK resource, designed by the authors to take place over 90 minutes (two class periods) at a high school in Thessaloniki, Greece, in a class of 26 students of 11th grade (12 boys, 14 girls, age 16), who specialized in Mathematics and Science in November, 2019. The teacher was given instructions (see Design and Implementation of the activity below) while being observed by the author.
Design and integration of the activity
An external view of the Black Box is shown in Figure 1, and its internal structure is shown in Figure 2.

The external view of the Black Box.
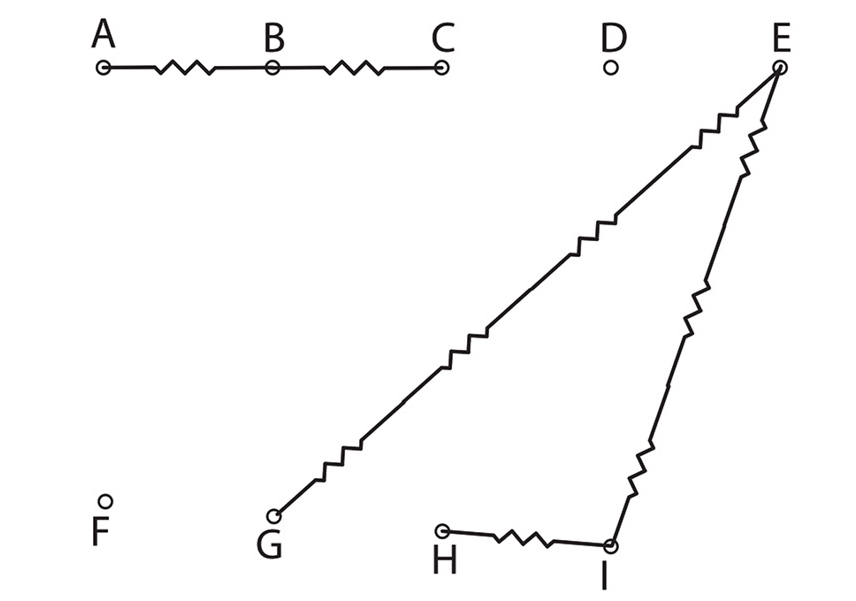
Structure of the Black Box.
AB = BC = CD = DE = FG = GH = HI = 5cm, EI = 15cm and EG = 20cm. Resistances of all resistors are 8.2Ω.
Materials
- The Black Box
- 4.5V cell
- 3.6V bulb
- piezoelectric buzzer
- three cables
- ohmmeter
- ruler
- compass
The problem
Introduce the problem to students: Some of the points A, B, C,… shown in Figure 1, are connected to each other, either directly or through other points. Find the exact way they are connected. Solve the problem working like a scientist who plans his/her investigations for a new discovery. Also, review your own work and search for NOSK aspects during your problem-solving. Think of the problem as more general, for example in proportion to a contemporary research problem, where (a) new instruments provide new data, (b) probable mathematical solutions are rejected and, finally, (c) creative thinking provides the answer through seemingly irrelevant/random observations.
Guidelines
- Students record their observations, using the instruments in the following order:
- Assemble the tester circuit shown in Figure 3, using your given materials. Place cables’ terminals 1 and 2 on points A, B, C,… and define which points are interconnected to each other.
- Replace the bulb with the piezoelectric buzzer on the tester circuit and repeat your previous investigation.
- Repeat the process, using the ohmmeter (±0.1Ω measurement uncertainty).
Notice: the ruler and/or the compass can be used if you consider doing so. You can ask for anything else you need.
The teacher divided the students into 6 groups, 4 groups of 4 students and 2 groups of 5. He started the lesson with a quick reminder of NOSK aspects for 5 minutes, that were taught in detail in a previous lesson. In the next 10 minutes, he explained the problem and gave the guidelines; the goals were to design the interior of the Black-Box and to recognize NOSK aspects that arise from the activity. He asked the students to start working, using the bulb as an instrument for 15 minutes, moving on to the buzzer for another 10 minutes, and then for 20 minutes to use the ohmmeter.
For each instrument, he asked students to discuss in their group and write down their observations and inferences. He informed them that their notes were necessary for the plenary discussion, which took place in the last 30 minutes of the lesson. To achieve the goals of the activity, the teacher directed the discussion and set the appropriate questions (see Online Connections, 4th and 6th column of Figures 4–6 respectively). During the inquiry, the teacher was available for technical support and reminded students to switch to a different instrument when the time came.
Students followed the instructions, discussed in their groups, and kept notes on their group decisions. Then, they discussed in the plenary their findings and exchanged arguments with their peer students, following the teacher’s questions.
In order to provide a full description and highlight the connections between observations, inferences, questions during discussion, etc. the entire implementation is presented in Figures 4, 5, and 6 (see Online Connections), one per instrument used (bulb, buzzer, ohmmeter). For each figure:
- Column 1 lists the points combination for which at least one of the three instruments show an indication.
- In column 2, those indications are presented when connected to respective points. The bulb’s illumination is altered due to the resistor between the two connected points. It was decided to use 8.2Ω resistors to achieve gradation on the bulb’s illumination. The buzzer’s sound intensity does not change by adding a few ohms in series (on the direction that conducts electricity), because its internal resistance is 3.5MΩ.
- The inferences that students could ideally make from observations of the second column are presented in column 3.
- Questions asked to students during plenary discussion to encourage them to present their own inferences (individual or group ones) are in column 4. We decided not to give those questions in the beginning, in order to do an open inquiry.
- Expected key points from plenary discussion and presentation of inferences are presented in column 5.
- For every key point, the question “which NOSK aspect can you identify here?” is asked. The expected answer is presented in column 6. For example, in Figure 4, the question “Are E-G conductively connected?” may have multiple answers from students. The mention of these answers (yes/no/not sure) during the plenary discussion may, through the above question, lead to A1 NOSK aspect.
Students’ reaction—plenary discussion
Students participated actively. After the observations from each instrument, they discussed in their groups and sketched a draft of the connection between the points. All groups mentioned that they found new connections when changing from the bulb to the buzzer. The ohmmeter made those connections clearer. The evolution of one group’s inferences is shown in Figure 7.
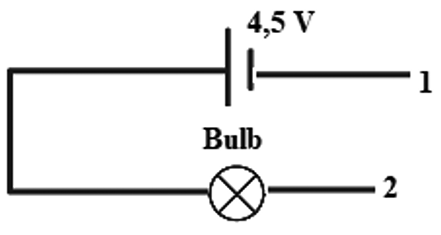
Tester circuit.
Four out of six groups ended up with the circuit connections shown in Figure 7. One developed a more complex connection on points E-H-G, and one was wrong. It is very interesting that one group, during processing, ended up with the observation that the resistance of a branch is proportional to the length of its respective segments (the “Law,”) and claimed that resistors are not possible to be on branch E-H, based on the points’ distance. One group suggested the alternative possibility of a resistor being on the branch E-H, but did not complete the mathematical solution, something the instructor did. It was discussed that in science there might be a mathematical solution, but it could be rejected from observations.
For students who did not use “Law,” the instructor asked them to notice the values of their measurements for segments AB, BC and IH and formulate a hypothesis for the value of the resistor in relation to the length of respective segments, and then check the hypothesis on the other connections.
Finally, during discussion, a group suggested connecting a battery to points E and H, and place the compass on the segment, to see if it deviates. That could not happen, even if there was a resistor between E and H, due to the low current. Nevertheless, it is an interesting creative thought.
Key discussion points, similar to the tables’ column 5, plus the question “which NOSK aspect can you recognize here,” led to the explicit recognition of NOSK aspects (column 6). Students liked the activity, especially the potential to extract new data by using a new instrument. The dependence of the production of scientific knowledge on financial factors was also discussed (for example in particle accelerators), regarding the supply of equipment and some research centers’ superiority.
Inclusion and differentiation
The activity is designed for all students. Written guidelines are very short, and the teacher spends 10 minutes presenting the problem and the guidelines, using the same objects students will work with. The questions can be answered correctly by students of different abilities; for example, when the tester circuit is connected between two points and bulb does not illuminate, one student could infer that the two points are not connected, another could claim that a high resistor interferes between the two points, and another can suggest both possibilities. It is important that all students can participate in the discussion, through which NOSK aspects are determined.
More observant students could formulate a hypothesis for the value of the resistance in relation to the length of the respective segments and end up to the law (as occurred in one group). Students more skillful in mathematics could move on to the mathematical solution for the existence of a resistor in the branch E-H (something that did not occur in any group). Finally, it is important that students are divided into groups of mixed abilities, to ensure collaboration among students of different abilities.
Safety issues
The voltage used in this activity is very low and not dangerous for the students. However, the teacher should remind students that when working with electric circuits, they should use only batteries or other electric sources that provide the voltage specified in the worksheet. Avoid short-circuits and do not connect the battery to the points of the Black Box without having connected the bulb or the piezoelectric buzzer, as seen in Figure 3.
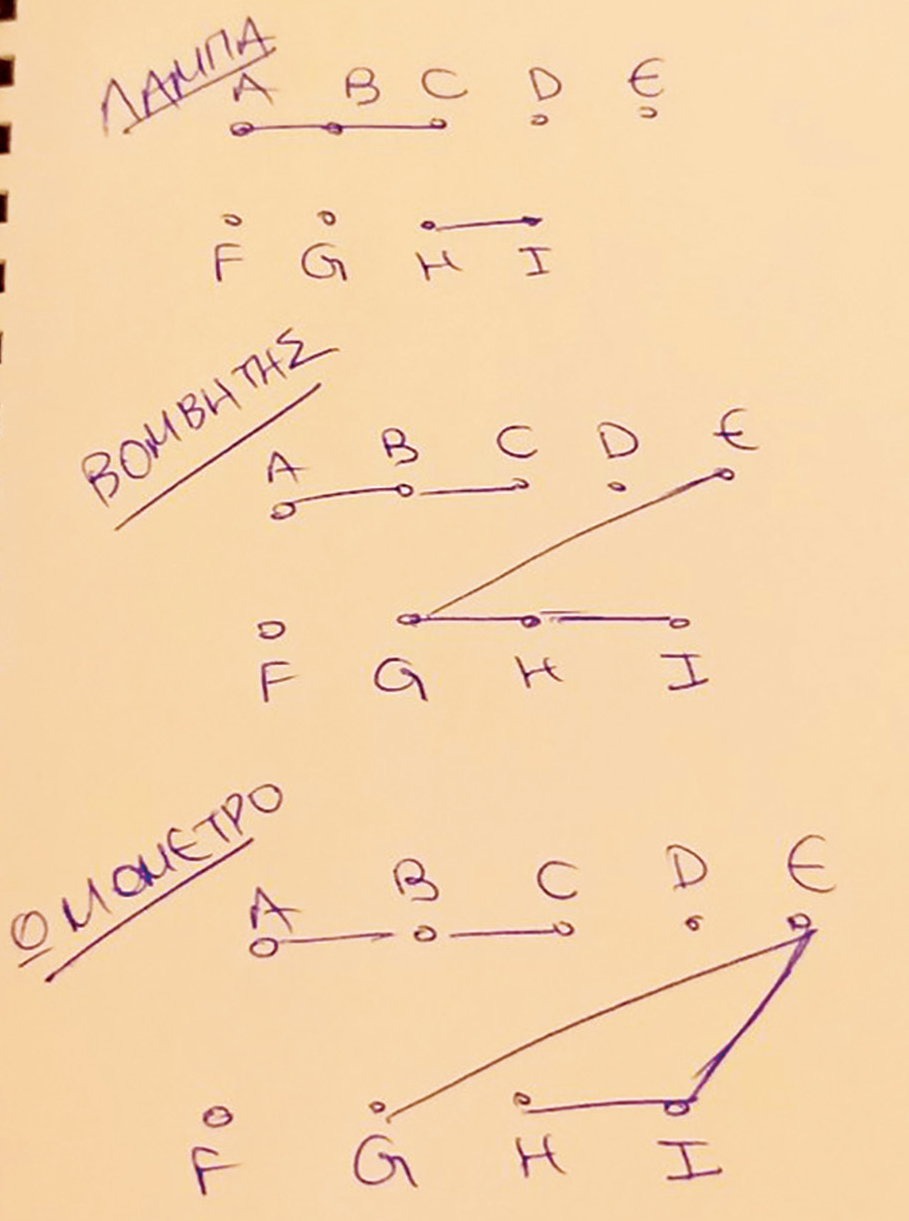
Draft sketch of one group on connectivity between points for bulb, buzzer, and ohmmeter respectively.


Students during work.

Black Box construction instructions.
To construct the Black Box, we used 8.2Ω, 1W resistors, tolerance 5%. Using an ohmmeter, we chose among the ones we bought those that reach the value 8.2Ω. Resistors are connected to each other using an electric soldering iron. The electric circuit is attached to a foam board, using tape. Then, it is closed with a properly cut piece of the foam board, which is laid on supports, as seen in the Figure below. The final shape is shown in Figure 1. The points A, B, etc. shown in the figure are terminal male connectors with solder placed above them. The values of the resistors (8.2Ω) and the voltage (4.5V) used, are chosen for the desired gradation in the illumination of the bulb.
Assessment
By the end of the lesson, students are expected to:
- Realize that different inferences may come out of the same observations.
- Acknowledge that the usage of new instruments contributes to the change of scientific knowledge.
- Comprehend the role of creativity in the configuration of the scientific endeavor, even when evidence from existent instruments is not enough.
- Design models based on their observations and exchange arguments for and against one model.
As for formative assessment, the teacher can get evidence through the discussion of the inquiry and encourage more students to participate. Alternatively, by the end of the lesson the teacher can ask students to write on a piece of paper, and deliver it, two things they were impressed about from the lesson, two they were concerned about, and something they learned and consider important for their everyday life. If the teacher regards it necessary, he/she can give one or two questions (due to time restrictions) from the VNOS-D+ questionnaire (https://www.physport.org/assessments/assessment.cfm?A=VNOS), like question 4 (especially 4b and 4c), or question 6. Both questions suit the Black-Box activity since scientists cannot conduct direct observations.
Conclusion
In the Black Box lesson, we used an active, cooperative, inquiry-based approach, targeting NOSK aspects. We focused on the significant role of the instruments’ evolution, as well as human imagination in problem solving. We discussed extensively how the same observations may lead to different inferences. We hope it will contribute, along with similar lessons, to students’ future understanding that scientists’ change of view, or the different views among scientists, is not due to human mistakes but something inherent to science.
Online Connections
Figure 4. Study of the Black Box, using the bulb as an instrument: https://bit.ly/3LkfHNA
Figure 5. Study of the Black Box, using the buzzer as an instrument: https://bit.ly/3qHxjee
Figure 6. Study of the Black Box, using the ohmmeter as an instrument: https://bit.ly/36Brath
Anna Koumara (anniekmr@gmail.com) is a researcher and Katerina Plakitsi (kplakits@gmail.com) is a professor in the Department of Early Childhood Education, University of Ioannina, Greece. Norman Lederman was Distinguished Professor of Mathematics and Science Education at the Illinois Institute of Technology, Chicago, IL.
Engineering Instructional Materials Makerspace High School


