Teaching Teachers
Integrating Computational Modeling Into Science Instruction With English Learners
Science and Children—May/June 2021 (Volume 58, Issue 5)
By Alison Haas, Scott Grapin, Katie Simon, Lorena Llosa and Okhee Lee
When we first began integrating computational modeling into our science instruction, we saw students compelled to do science in ways that reignited our passion for science teaching. Computational models, or “representations of phenomena that can be simulated by a computer” (Weintrop et al.,2015, p. 137), enable students to enhance their understanding of phenomena by exploring and testing the behavior of complex systems. As computational models are becoming more widely used with the release of A Framework for K-12 Science Education (National Research Council 2012) and the Next Generation Science Standards (NGSS; NGSS Lead States 2013), these models are reshaping the way science is practiced in increasingly diverse classrooms. For students classified as English learners (ELs), who make up a sizable and fast-growing subset of the student population, computational models provide a powerful resource for communicating science ideas and fostering productive discourse in classroom communities.
The purpose of this article is to describe why and how teachers can integrate computational modeling into NGSS-aligned science instruction with all students, including ELs. First, we describe the benefits of computational modeling and how teachers can integrate computational models into science instruction in a way that complements other model types they already use in their classrooms. Second, to illustrate these benefits, we describe how one fifth-grade teacher, Ms. Simon, integrated computational modeling into her science instruction. Specifically, we highlight how the affordances of different model types (physical, diagrammatic, computational) allowed all students, including ELs, to explain the phenomenon of garbage and develop deep understanding of physical and life science core ideas. Finally, we offer recommendations for teachers interested in integrating computational modeling into their science instruction with all students.
Why Computational Modeling
Modeling is a central practice of scientists and engineers and one of eight science and engineering practices (SEPs) articulated in the Framework and the NGSS. In the NGSS classroom, students engage in three-dimensional learning as they develop models (SEP) in combination with crosscutting concepts (CCCs) and disciplinary core ideas (DCIs) to construct increasingly sophisticated explanations of phenomena. While modeling is an important practice for all students, ELs in particular benefit from using multiple meaning-making resources (e.g., drawings, symbols, code) beyond just language to communicate their ideas (Grapin, 2019).
With the emphasis on modeling in the NGSS, teachers are integrating different model types into their science instruction. These include both physical models (i.e., models constructed using physical objects or events) and diagrammatic models (i.e., models constructed using drawings, symbols, and text), with each model type presenting distinct affordances and limitations. For example, students can use physical models to make observations that produce data (i.e., an affordance), but these models do not show invisible processes underlying phenomena, such as matter particles (i.e., a limitation). Given this limitation, students can also develop diagrammatic models to represent invisible processes (i.e., an affordance). However, while diagrammatic models frequently make use of symbols (e.g., arrows) to indicate movement, the static nature of these models makes it difficult to show certain dynamic aspects of phenomena, such as solid particles changing into gas particles (i.e., a limitation).
Computational models (i.e., models constructed using a computer) provide affordances that address some of the limitations of physical and diagrammatic models. Specifically, computational models allow students to represent invisible agents (overcoming the main limitation of physical models) while also giving those agents dynamic rules of behavior (overcoming the main limitation of diagrammatic models). Students can then run their computational models to test causal explanations of phenomena in ways that go beyond what is possible with physical and diagrammatic models. Furthermore, programming languages (i.e., code) used to develop computational models provide another powerful modality through which all students, including ELs, can communicate their ideas.
While computational models allow students to represent invisible agents and give dynamic behaviors to those agents, these models still need to be triangulated with other model types and data sources in order to construct explanations of phenomena. Thus, computational models are not meant to replace physical or diagrammatic models in science classrooms but to supplement and enhance the other model types. By integrating physical, diagrammatic, and computational models in complementary ways based on the affordances and limitations of each model type, teachers can create learning experiences that allow all students, including ELs, to develop deep science understanding. The affordances and limitations of the three model types are summarized in Table 1 and illustrated through a classroom example in the next section.
| Table 1. Affordances and Limitations of Different Model Types | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Integration of Computational Modeling Into Fifth-Grade Science Instruction
In this 9-week instructional unit, which addresses NGSS performance expectations (PEs) in physical and life science (see Table 2 at the end of the document), students explain the phenomenon of garbage in their school, home, and community in order to answer the driving question: What happens to our garbage? We describe how one fifth-grade teacher, Ms. Simon, implemented the unit in her linguistically diverse science classroom. Specifically, we highlight how Ms. Simon’s class used physical, diagrammatic, and computational models in ways that leveraged the affordances and addressed the limitations of each model type (see Table 1).
The class developed physical models in Mason jars to observe what would happen to different garbage materials over time (Figure 1). Half of the students closed their landfill bottles, while the other half left their bottles open, creating open and closed landfill bottle systems (Safety guidelines for this investigation can be found at www.nyusail.org). Over several weeks, students recorded the properties, including the weight, of the open and closed landfill bottle systems. After making observations at multiple time points, students figured out that the weight of the open landfill bottle system (but not the closed system) decreased because the smell of the decomposing food materials left the open system. This leveraged an affordance of physical models by allowing students to make observations that produce data (e.g., the weight of the open and closed systems). ELs in particular benefited from using gesture and concrete resources in the situation to communicate their observations (e.g., pointing at the measurement scale while saying, “The closed bottle stayed the same”). At the same time, Ms. Simon guided the class to recognize a limitation of their physical models, namely, that these models did not show invisible processes underlying the phenomenon of smell.

Physical models of landfill bottles in open and closed systems.
After carrying out a series of investigations related to the particle nature of gas, students developed diagrammatic models that showed smell particles moving freely out of the open system but remaining inside the closed system (Figure 2). All students, and ELs in particular, benefited from using drawings and symbols (e.g., dots with arrows in random directions to represent particles moving freely) to communicate their ideas. Using their diagrammatic models, students argued that the smell particles leaving the open system accounted for the decrease in weight that they observed in their physical models. Thus, students leveraged an affordance of diagrammatic models by representing invisible processes underlying the phenomenon of smell (i.e., smell particles moving freely). At the same time, Ms. Simon guided the class to recognize a limitation of their diagrammatic models: Although these models included arrows to indicate the movement of smell particles, they did not show the dynamic process by which solid food materials get decomposed and change to smell particles that leave the open system.
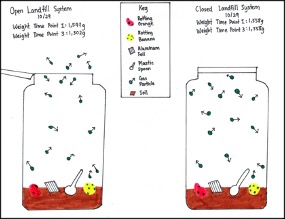
Diagrammatic model of landfill bottles in open and closed systems.
Enter computational modeling! Before developing their computational models, students obtained information from an article describing how the decomposition of food materials is caused by a type of decomposer called microbes. Ms. Simon suggested that the class could develop computational models to explain the invisible process by which microbes caused changes to food materials in their physical models. To develop their computational models, students used StarLogo Nova (SLN), a blocks-based programming environment that allows students to program agents and their interactions by assembling code blocks.
In pairs, students developed computational models using a class set of laptops to explain decomposition by microbes. Specifically, they focused on modeling the closed landfill bottle system. Figure 3 shows the code blocks assembled by one partner group, Rafael (an EL) and Deborah (a non-EL), to represent microbes decomposing a banana. Rafael and Deborah were excited to program their idea that each microbe, upon colliding with one banana solid, deletes (i.e., eats) the banana solid and creates one banana gas (Figure 3). They also programmed the banana gas, once created, to move forward in random directions to represent smell particles moving freely. The use of code blocks allowed all students in this class, and ELs in particular, to communicate abstract science ideas that might have otherwise been difficult to communicate with language alone.
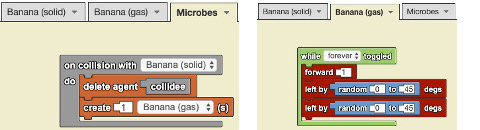
Code blocks for computational model of decomposition by microbes in closed landfill bottle system.
Next, Rafael and Deborah ran their computational model (Figure 4). In addition to showing the agents and their interactions (see right side of Figure 4), the computational model displayed data boxes (see top left corner of Figure 4) that kept track of the weight of the banana gas, the weight of the banana solid, and the total weight of the banana in the closed system. When Rafael and Deborah noticed that the total weight of the banana remained the same (i.e., 500) even as the banana solid changed to banana gas, Rafael made a connection to his physical model: “All of it [the matter] is still in there – just like the actual landfill bottle!”

Computational model accurately depicting decomposition by microbes in closed landfill bottle system.
Other students noticed that their data boxes did not match the data produced by their physical models. For example, one pair programmed the microbes to delete the banana solid but not to create banana gas (Figure 5). When these students ran their computational model, they noticed that the total weight of the banana decreased (i.e., from 500 to 254), indicating that matter was not being conserved in the closed system. These data prompted the pair to rethink decomposition by microbes and revise their computational model. The opportunity for students to run their computational models and get immediate feedback on whether those models reflected the ideas they were attempting to communicate was particularly beneficial to ELs.

Computational model accurately depicting decomposition by microbes in closed landfill bottle system.
As students developed their computational models, Ms. Simon engaged in informal formative assessment by attending to partner discourse and asking probing questions to push students’ thinking forward. For example, in the case of one group who was unsure of how to use the data produced by their model, Ms. Simon asked, “How do the weight data in your computational model compare with other data you’ve collected in this unit?”
Ms. Simon’s students leveraged an affordance of computational models by representing invisible agents (i.e., smell particles) and giving those agents dynamic rules of behavior (i.e., microbes collide with the banana solid and create banana gas particles that move freely in the closed system). However, their computational models still needed to be triangulated with other model types and data sources (i.e., the physical model and the article about microbes) in order to explain decomposition by microbes. By comparing the data produced by the computational model with the data produced by the physical landfill bottle model, students were able to determine whether they had faithfully represented how microbes decompose food materials. Thus, using multiple model types in combination provided greater explanatory power than any model alone and allowed all students, including ELs, to develop and communicate their science understanding.
At the end of the unit, Ms. Simon used multiple sources of information to assess her students’ understanding, including their final diagrammatic and computational models as well as their written explanations in response to the following question: How do microbes cause changes to food materials in the landfill bottles? (see Figure 6 for a rubric to assess this explanation).
Recommendations for Teachers
One question we are often asked is how computational models relate to the computer simulations that many teachers already use in their science classrooms. Computational models indeed share some similarities with these simulations. For example, both computational models and simulations allow students to run tests over multiple trials. However, computational models also present distinct affordances where simulations fall short. For example, whereas simulations typically consist of premade representations with adjustable parameters, computational models allow students to construct their own representations by programming agents and their interactions. Through actively constructing their models, students develop deep understanding of the causal mechanisms underlying phenomena. Also, by allowing students to make crucial decisions about how to represent their ideas, computational models promote authentic engagement in the science modeling practice. We believe that these affordances of computational models make integrating computational modeling into science instruction a worthwhile endeavor. We provide the following recommendations for teachers interested in undertaking this work with all students:
Capitalize on student engagement with technology (Our students ask to work on their computational models even during recess!). Consider where in your science curriculum would be most high-leverage to integrate a computational model given the particular affordances of this model type (see Table 1). The goal is purposeful integration, with science learning goals driving the use of technology (and not the other way around).
Become familiar with a blocks-based programming environment. SLN (www.slnova.org) is free, open-source, and accessible to elementary students. It won’t be long before your students are teaching you (and that’s okay!).
Rather than have students develop their computational models from scratch, provide a “starter model” that students can modify or adapt. The starter model for the classroom example above included the solid banana and data boxes (https://sailctm.slnova.org/ams728/projects/685901/). Then, students modified this model by programming their ideas about how microbes would interact with the solid banana.
Have students develop their computational models in pairs (two students per computer). ELs in particular benefit from interactions that involve a joint frame of reference (e.g., pointing at the screen while talking with a partner). If you do not have access to a class set of laptops or a computer lab, consider co-constructing a computational model with your students on a screen in front of the classroom.
Online Connections
Table 2—Connecting to the Next Generation Science Standards
Alison Haas (ams728@nyu.edu), Scott Grapin, and Lorena Llosa are professors at New York University–Teaching and Learning. Catherine Simon is a teacher with Elizabeth Public Schools, Elizabeth, NJ. Okhee Lee is a professor at New York University.
Computer Science Earth & Space Science Multilingual Learners Environmental Science NGSS Elementary Grade 5


