focus on physics
Aha! Moments in Sun and Moon Measurements
Most of the physics we teach begins with Galileo, and rightly so. However, some good physics occurred centuries before Galileo; the achievements of Eratosthenes and Aristarchus are a worthwhile introduction to almost any physics course.
Aha! moments with Eratosthenes
Eratosthenes calculated Earth’s circumference in about 235 BC. That early date raises some eyebrows, and is in itself an Aha! moment. To understand his method of measurement, consider the geometry of a circle (Figure 1). A sample sector with a vertex angle of θ degrees is shown. How many vertex angles θ make up a full 360° circle? We’ll soon see that once the vertex angle θ and distance d are known, the circumference of the circle is then easily calculated. The same is true of a sphere, and particularly, spherical planet Earth.
Eratosthenes knew arc distance d between the cities Alexandria in the north and Syene in the south to be 800 km (in today’s measurement). If he had known Earth’s vertex angle θ, he’d have been able to calculate Earth’s circumference. He knew from library information that the Sun is directly overhead the city of Syene at noon during the summer solstice, made evident by water in a deep well there that reflects sunlight straight upward at that special time. At the same time, he measured the 7.2°angle that sunbeams made with a vertical pillar in Alexandria. (It’s interesting to note that such simultaneity today is easily achieved with a smartphone!)
Figure 2 shows that the 7.2° sunbeam angle Eratosthenes measured in Alexandria is also the vertex angle at Earth’s center. This is explained in my article “When Our Round Earth Was First Measured” in the September 2016 issue of The Science Teacher. More recently, Eratosthenes’s measurements tailored to a collaborative activity for distant high schools is treated in “Calculating Distances Via Flagpole Shadows” in the September/October 2020 issue of this magazine.
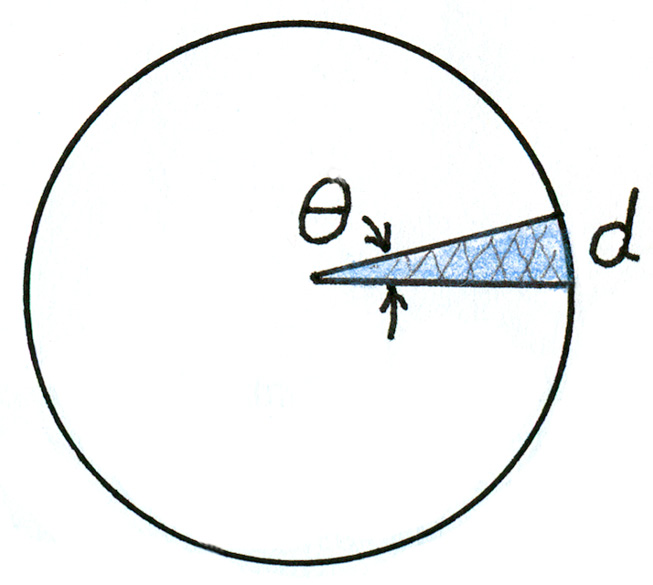
The pie-shaped sector of angle θ subtends arc distance d.
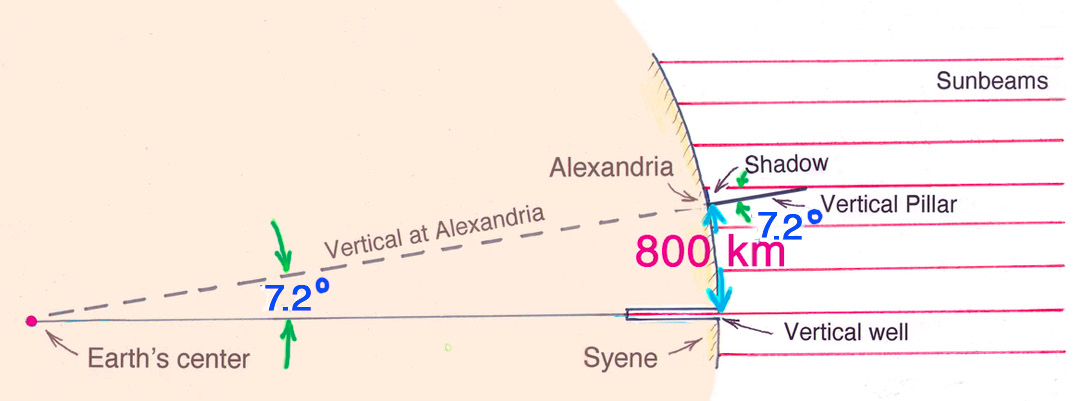
Eratosthenes’s experiment.
The key question is this: How many 7.2° segments make up a 360° circle? Simply answered, 7.2° is 1/50 of a circle. Is this a big deal? Very much so, for it means the circumference of Earth must be 50 times the distance between Alexandria and Syene—a big Aha!
Some related history
Eratosthenes’s findings were known to Christopher Columbus when he embarked on his 1492 voyage across the Atlantic Ocean. But Columbus ignored Eratosthenes, and instead chose to heed popular speculative maps that suggested a smaller Earth. Due to his error in judgment, Columbus believed the island he first set foot on was close to China. If Columbus had heeded Eratosthenes, he would have realized that he had reached a continent previously unknown to Europeans. A very big Aha!
Distance to the Moon
Another great Aha! moment can occur when you have your students perform an activity that approximates the distance from Earth to the Moon. When a full or nearly full Moon is apparent in the sky, have your students, with one eye closed, hold a pea at about arm’s length to just barely eclipse it. (A sphere larger than a pea would eclipse at a distance beyond arm’s length.) Careful measurement will show that about 110 peas could fit between the pea at arm’s length and one’s eye (Figure 3). Both the pea and the Moon subtend the same small angle, which is about 0.5°.
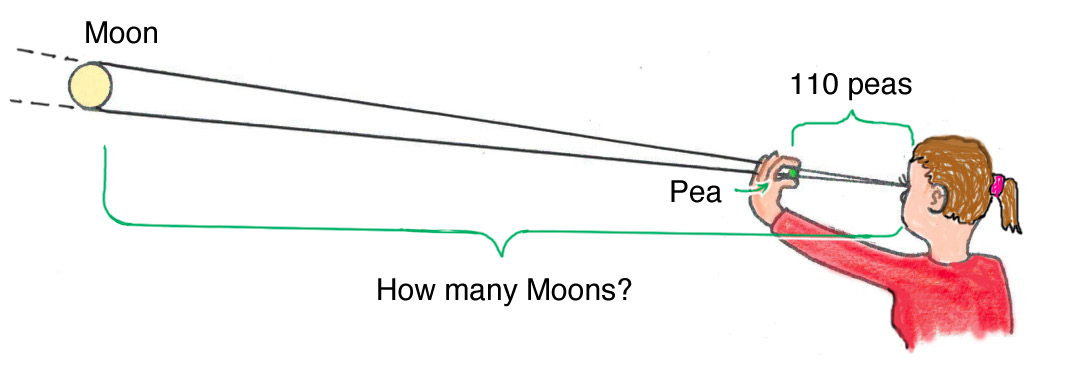
The pea-Moon experiment.
How many moons can fit between Earth and Moon?
Get ready for a huge Aha! This question has rarely been thought about by the greatest minds—but you can confront your students with it! The answer, perhaps realized right away or after some discussion and sketching, or collaboration with study buddies, is the same: 110 Moons! Student realization that the same number of Moons would fit between its location and the observing eye as the number of peas between the pea at arm’s length and the eye is a giant accomplishment in thinking. And a huge Aha!
Distance to the Sun
It’s interesting to note that no physical reason accounts for the Sun and Moon appearing the same size in the sky. I often quip with students that answering a question as, “just the way it is,” is unscientific. However, a big exception occurs with the sheer coincidence of equal sizes of the Moon and Sun in the sky (A small Aha!). In times past the Moon was appreciably closer to Earth. In future years it will be farther away. The reason for this involves the conservation of angular momentum and friction between ocean waters and the ocean floor, which we’ll not discuss further here.
At the present time the Sun and Moon subtend equal angles of about 0.5° in the sky. This relates to the 110 moons that would fit between Earth and the Moon. With this knowledge you can pose this question: How many Suns could fit between the Sun and Earth? Another Aha! The same 110! We know that the distance to the Sun is enormous and we now get a better idea of this vast distance. You can put it this way: Our Sun is 110 Suns away from Earth! A true gem!
Aristarchus and the Sun
Shortly after Eratosthenes’s discovery of Earth’s size, the Greek astronomer and mathematician Aristarchus used simple trigonometry to calculate the Sun’s distance from Earth at the special time when the Moon was half full—when the Moon, Earth, and Sun form a right triangle—another Aha! (Figure 4).
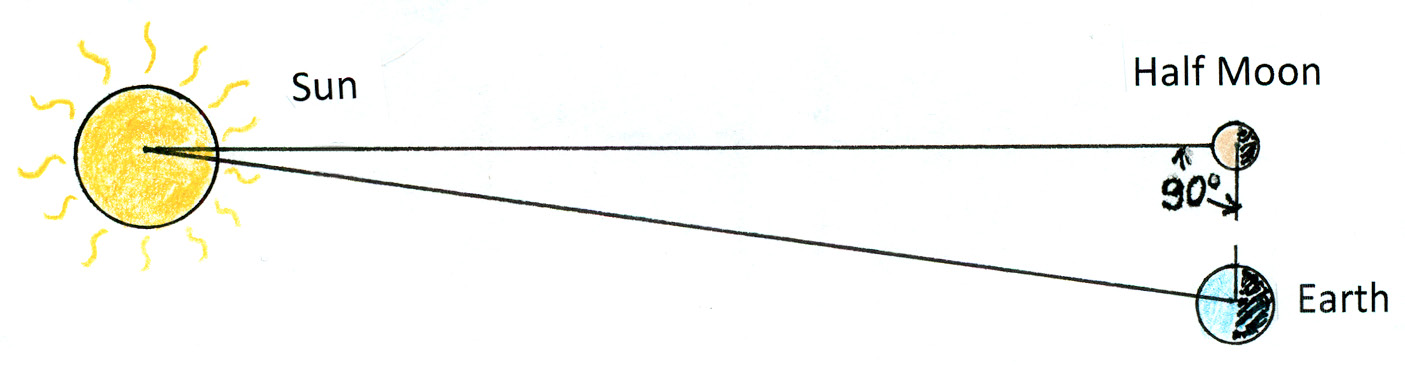
A right angle occurs for lines of sight during a half Moon.
A rule of trigonometry states that if you know all the angles in a right triangle plus the length of any one of its sides, you can calculate the length of any other side. Aristarchus knew that one angle of the triangle was 90°. He also knew the distance to the Moon. Measuring the second angle was difficult to do without a modern transit. He calculated that the Sun was about 20 times more distant than the Moon, when it’s actually almost 400 times farther away. Nonetheless, Aristarchus is greatly admired for his ingenious method. For myself, and for some students, the Aha! lingers for life whenever a half-Moon is observed in the sky. Hooray to Aristarchus!
On the web
See complementary student tutorial screencast 149 on www.HewittDrewIt.com, and www.ConceptualAcademy.com.
Paul G. Hewitt (pghewitt@aol.com) is the author of Conceptual Physics, 13th edition; Conceptual Physical Science, 6th edition, coauthored with daughter Leslie Hewitt and nephew John Suchocki; and Conceptual Integrated Science, 3rd edition, with coauthors Suzanne Lyons, John Suchocki, and Jennifer Yeh.
Earth & Space Science Physics Teaching Strategies High School



