feature
From User to Creator
Helping Students See Inside the “Black Box” with Insight Maker
The Science Teacher—January/February 2022 (Volume 89, Issue 3)
By Amanda Gonczi, Chuck Palosaari, Alex Mayer, and Noel Urban

Computational modeling and thinking skill sets were previously relegated to computer scientists and programmers. As a result, computational tools are largely unfamiliar to K–12 science teachers and students (Yasar and Veronesi 2015). However, Janet Wing (2006) highlighted how computational thinking is not unique to the computer science field. Rather, it is inherent to many science and engineering disciplines as well as everyday activities. In the current digital age we are all consumers of computational products such as simulations and models that predict everyday events, including weather, disease transmission, and economic growth. These products aren’t magical—students should understand how they are developed, their limitations, and their capabilities. As a result of these considerations, Using Mathematical and Computational Thinking and Developing and Using Models were included in the Next Generation Science Standards (NGSS) as core science and engineering practices (SEPs) (NRC 2012).
The NGSS lays out a progression for Using Mathematical and Computational Thinking that, in elementary school, includes familiar activities such as making quantitative comparisons, creating graphs, and using computer simulations. By high school, students should advance and be able to create or revise simulations using algorithms—mathematical and computational tasks that are far less familiar to both students and teachers (NGSS Lead States 2013). Similarly, there is a progression from using to developing computational models (NGSS Lead States 2013).
The lesson that follows is designed to assist students and teachers to move from the familiar (simulation user) into less-explored territory (simulation creator). The lesson was implemented in a high school STEM elective course and consists of four 55-minute class sessions that help students develop greater proficiency in the two targeted SEPs. The lesson uses two open-source software tools: Concord Consortium and Insight Maker. Students first use a computational representation to illustrate the relationships among Earth systems and how those relationships are being modified due to human activity (HS-ESS3-6) and then (2) develop a model based on evidence to illustrate the relationship between systems or components of a system (HS-LS2-5).
Day 1. Using a simulation to develop a conceptual model
The lesson is introduced through student use of an open-source simulation from Concord Consortium that addresses Earth science content; specifically, the simulation supports students’ ability to answer the research question, “How does Earth’s atmosphere affect the radiation energy balance?” Students are guided through simulation use via software-embedded questions and instructions. During this part of the lesson, students work in pairs and share a computer. To avoid aimless clicking, students should have instructional support (guiding questions and teacher guidance) during simulation use to help them focus on germane information that supports conceptual understanding (Gonczi and Chiu 2016). Teachers should circulate through the room and ask students probing questions including, “What relationships are you observing? What components of the atmosphere seem to affect Earth’s energy balance? How could human behavior change the atmosphere and affect the energy balance?”
Following simulation use, students consider whether they can use the simulation to create a conceptual model of Earth’s radiation energy balance. In pairs, students create conceptual models on whiteboards to facilitate comparison and discussion between groups (Figure 1).

Three student-generated conceptual models of radiation balance on the Earth.
After students complete this step, the teacher guides students to consider the following questions: How could conceptual models be used to inform the development of a simulation? How are simulations and conceptual models similar? How are they different? Appropriate answers to the questions include the following: Both types of models can help make sense of scientific phenomena and evaluate claims; conceptual models emphasize connections but do not account for mathematical relationships; simulations can account for mathematical and predictable relationships between variables that support a user’s ability to make predictions and test hypotheses. While this part of the lesson can be done as a whole-class discussion, teachers may want to have students record their answers to the prompts so that students can revisit and revise them at the end of the lesson.
Day 2. Computational models and Insight Maker
The goals for this part of the lesson are for students to realize that (a) computer simulations are produced through computational modeling, and (b) the final simulation is only as good as the conceptual and computational models that shape it.
For students to begin computational modeling, they must know the language of modeling; here we use terms (stocks, flows, variables—all primitives or system model components) used within the Insight Maker software. After reviewing the definitions in Table 1, groups classify Day 1 conceptual model components as either a stock, flow, or variable before being introduced to Insight Maker.
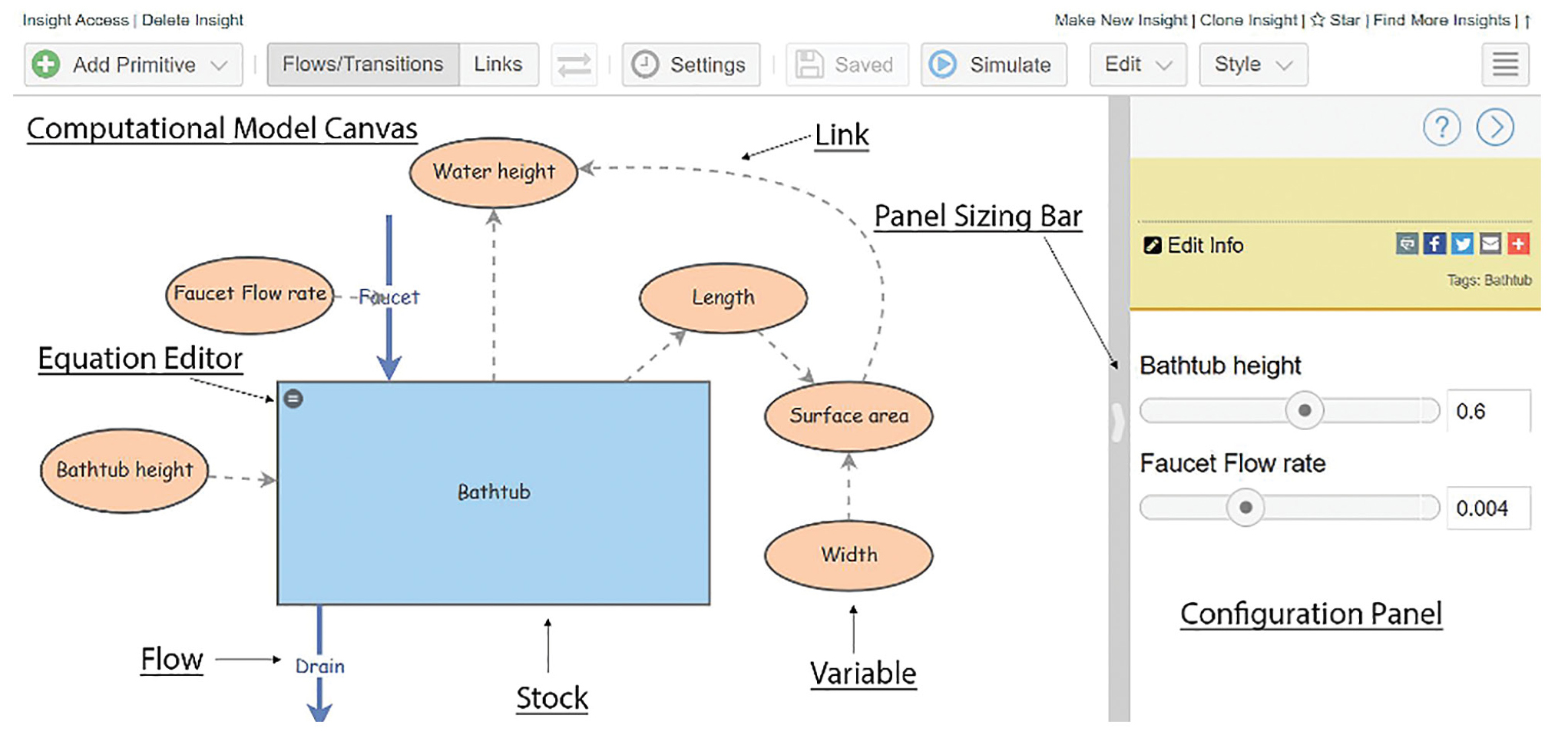
Insight Maker (https://insightmaker.com) is an open-source modeling tool designed to be accessible to the general public (Fortmann-Roe 2014). Anyone can create a free account that allows them to make “Insights,” or computational models. The website has a variety of help tools including a user manual and videos. When a student builds an “Insight,” the screen is split into two parts. On the left-hand side, users build conceptual models with stocks, flows, and variables. Computational additions are shown on the right-hand side of the screen in the configuration panel. The size of each panel can be adjusted by dragging the gray bar that divides them (Figure 2).
| Table 1. Definitions and examples of computational model components. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Sample argumentation discussion.
We recommend building a simple “bathtub” model with the whole class to introduce students to Insight Maker’s interface and improve students’ familiarity with relevant vocabulary. A bathtub model is first built by identifying primitives from the dropdown menu in the top left of the screen (Figure 2). A very basic model would have the bathtub as the stock, a faucet as a flow input, and a drain as a flow output. Characteristics of each of these components are defined by variables. For example, in Figure 2 you can see that the tub has two variables, “tub height” and “tub length.” Similarly, the faucet has a “faucet flow rate” and the drain has a “drain rate.” Variables are defined by clicking on the equal sign in each primitive, opening the equation editor, and inputting values or mathematical expressions in the configuration panel. All primitives can be connected by dragging the arrow inside the center of each to the one you want to connect with.
In the whole-class demonstration of building a bathtub model, we initially have the bathtub filling indefinitely by programming the model such that the drain has a stopper (no water outflow) and a constant water inflow from the faucet. This outcome is graphically displayed by hitting the “simulate” button on the tool bar (Figure 3).
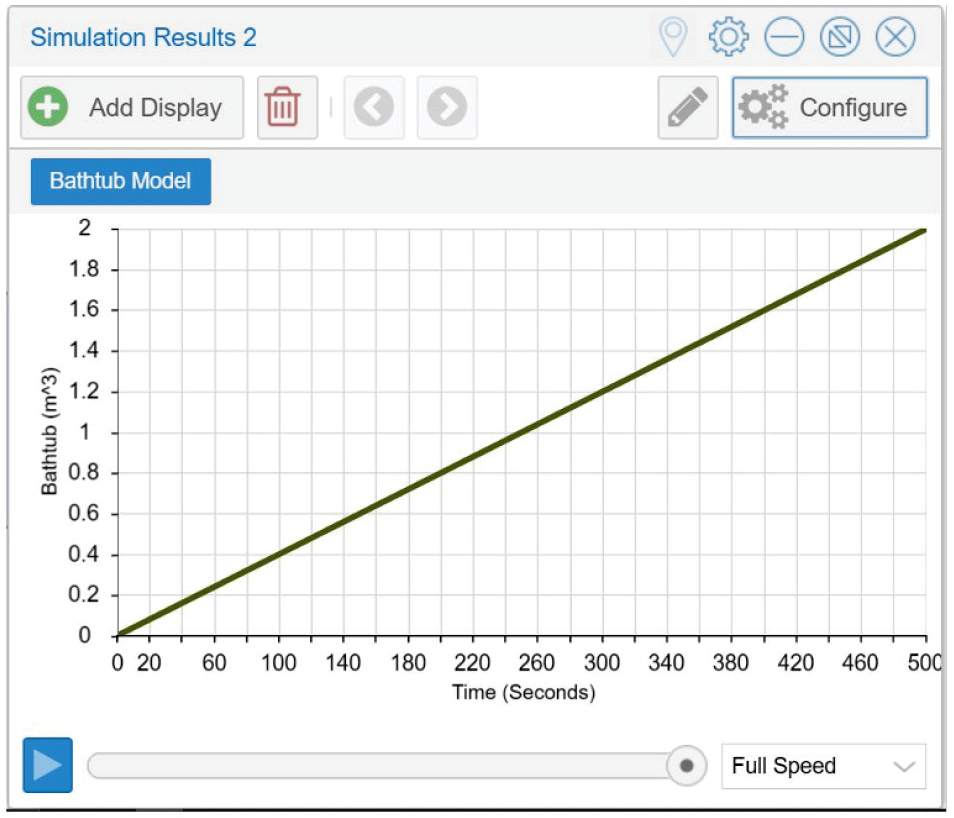
Graphical display of data based on computational model in Figure 2.
As a class, we discuss the problem with the model in Figure 2 based upon the output and brainstorm how the “plumbing system” might be redesigned to change the constant filling, which would ultimately lead to a flooded bathroom. One change is to have an overflow drain that is programmed with an “If, then, else statement” (Figure 4).
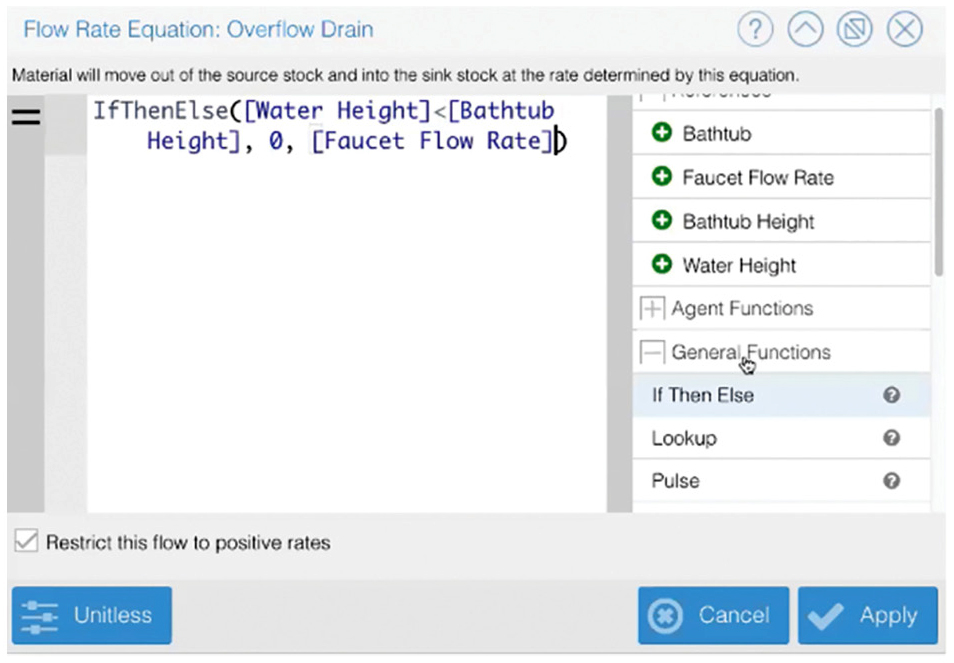
Programming the overflow drain with an “if, then, else” statement.
Insight Maker provides the basic syntax for basic programming commands so that users can simply input values within the given syntax. In this case, we told the overflow drain that the IfThenElse function is needed, where “if” the value of a stock or variable meets certain conditions, “then” modify the flow by a certain value. In Figure 4, the IfThenElse function compares the height of the water in the tub to the height of the bathtub. If the value of the water height is less than that of the tub, then the flow through the overflow drain will be zero. If the value of the water height is greater than the bathtub height, then the rate of flow out of the tub from the overflow will be equal to the rate of flow into the bathtub from the faucet flow rate. With this change, when the program runs, the graph shows the water level rising until it reaches the height of the bathtub at which point the output drain flow equals the faucet flow and the tub stops filling, as demonstrated by the horizontal line (Figure 5).
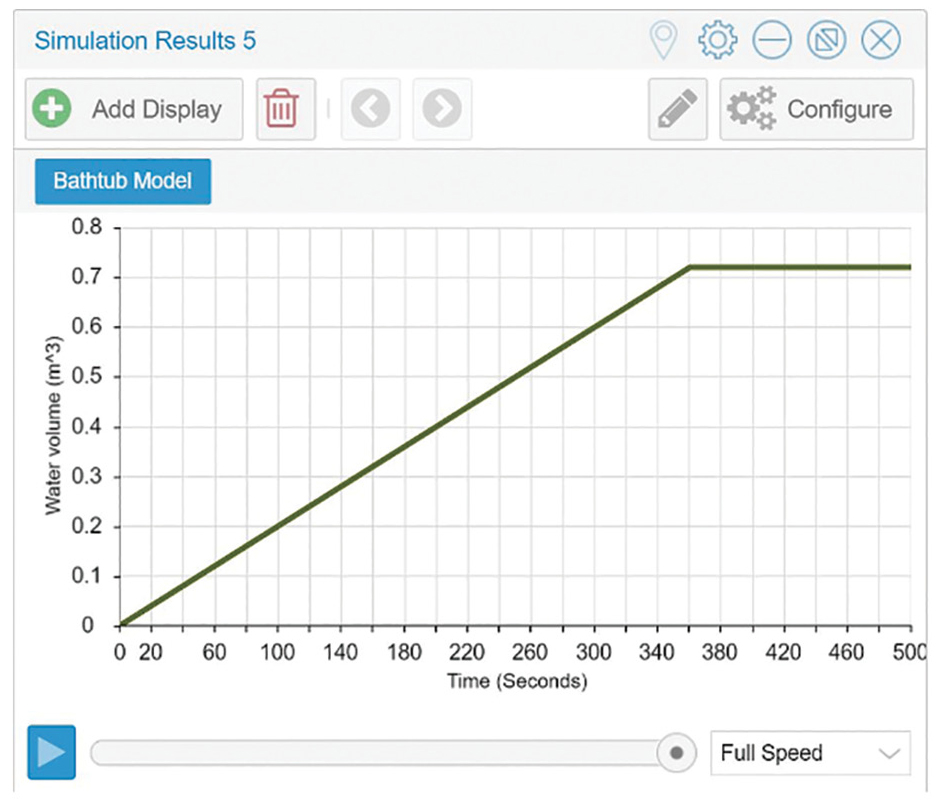
IfThenElse overflow drain function results.
Following this whole-class demonstration and discussion, students work on individual computers to create a working “bathtub” model. The student model can be the same one that was built as a group—or students may improve upon it. The purpose of this lesson segment is for students to show a basic ability to use the software to the extent it was modeled as a class. The teacher should move around the room to monitor progress and encourage collaboration among students.
Days 3 and 4: Using a real-world data set to build a computational model
At the end of the lesson students take what they learned the previous days and build a computational model of a real-world system in Insight Maker. This lesson was implemented in Michigan, where the predator-prey relationship between wolf and moose on Isle Royale is well studied and familiar to students. To determine the extent students could apply what they learned, they were provided the instructions and links to real-world data (see Appendix A). We had students work on individual computers, although collaboration with peers was encouraged to troubleshoot difficulties. Figure 6 shows one students’ model and simulated results.
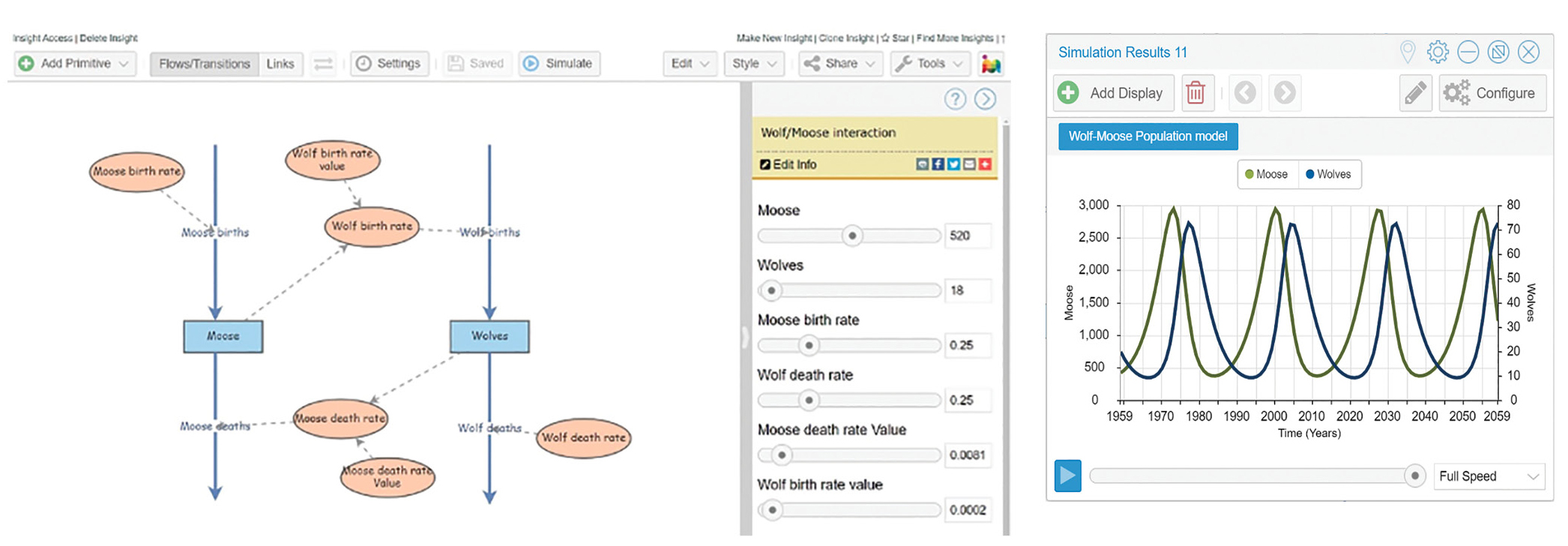
Students’ model of wolf and moose populations with graphical output.
Assessment
Students are summatively assessed using the rubric in Table 2 (see Online Connections) by evaluating whether their wolf/moose models work and by their responses to the questions on the worksheet (Appendix A; see Online Connections). In addition to this summative assessment, formative assessment can occur throughout the lesson and during small-group work as the teacher circulates and talks to students.
Implementation considerations and troubleshooting
The targeted SEPs were contextualized in familiar Earth and life science content. This was done so that students could focus cognitive energy on understanding the similarities and differences between computational and conceptual models, identify the affordances and limitations of each, and learn the basics of programming using Insight Maker. However, teachers can modify the lesson to introduce new content. Also, any system can be modeled within any science discipline.
We have found that students are accustomed to having software tell them—and sometimes even fix—text-related errors. However, Insight Maker does not fix students’ mistakes like Google Docs and other software. This poses a unique challenge to students; they have to troubleshoot their own work and debug what can be small, hard-to-find mistakes (such as syntax errors) that keep their models from functioning. As a result, we have found the bathtub model to be essential in giving students a first chance to be successful. We have also found it helpful to remind students they will need to pay attention to detail and not give up if the model doesn’t work right on the first try. In fact, model failures are not student failures, but opportunities to learn!
Conclusion
This lesson is designed to give teachers a blueprint for introducing and using the computational modeling software Insight Maker within their instruction to support proficiency in relevant performance expectations, especially those that include Developing and Using Models and Computational and Mathematical Thinking. The lesson provides students opportunities to formulate algorithms from conceptual models, turn algorithms into syntax, and make model improvements—all components of computational thinking. It also demonstrates that students and teachers can—without any previous computer science instruction—learn to use computational tools and include them within instruction to provide novel opportunities for their students to move from user to creator of simulations and gain deeper understanding of underlying science phenomena. ■
Online Connections
Table 2. Assessment rubric: https://bit.ly/3dCJiTv
Appendix A. Insight Maker instructions: https://bit.ly/3DFyoa4
Amanda Gonczi (algonczi@mtu.edu) is an Associate Research Scientist at Michigan Technological University, Houghton, MI; Chuck Palosaari is a science teacher in Adams Township School District, Painesdale, MI; Alex Mayer is a Professor at The University of Texas at El Paso, El Paso, TX; and Noel Urban is a Professor at Michigan Technological University, Houghton, MI.
Computer Science Engineering Labs Pedagogy Science and Engineering Practices STEM High School


