Research and Teaching
Students Taught by a First-Time Instructor Using Active-Learning Teaching Strategies Outperform Students Taught by a Highly-Regarded Traditional Instructor
Journal of College Science Teaching—March/April 2021 (Volume 50, Issue 4)
By Colin S. Wallace, Edward E. Prather, John A. Milsom, Ken Johns, and Srin Manne
In this paper we put forth a model for physics course reform that uniquely uses proven, research-based active-learning strategies to help students improve their physics knowledge and problem-solving skills. In this study, we compared the exam performance of students in two sections of the same introductory physics course. One section (the traditional section, N = 258) was taught by an instructor who is highly regarded for his lectures, but did not use any active-learning teaching strategies. The other section (the reformed section, N = 217) was taught by an instructor who had never before taught a physics class, but who was trained in physics and astronomy education research and who used active-learning teaching strategies. Students in the reformed section significantly outperformed students in the traditional section on common exam questions over the course of the semester, regardless of whether the question was conceptual or quantitative. This reform effort has been successful at improving students’ learning and significantly increasing the department’s use of active-learning strategies at the introductory level and beyond.
This paper describes an effort to reform a physics course and to transform a department’s attitudes toward active learning. In 2013, the University of Arizona became one of eight project sites funded by the American Association of Universities (2017) to redesign foundational STEM courses and to improve the attitudes of faculty toward active learning (Burd et al., 2016). As part of this effort, the Physics Department conducted a study comparing two sections of the same introductory physics course taught using drastically different instructional approaches. One section was taught by an experienced and highly regarded professor who used traditional lecture methods (the “traditional section”). The other was taught by a first-time physics instructor, versed in physics and astronomy education research, who used research-based active-learning strategies (the “reformed section”). In order to achieve the desired change in the department’s attitudes toward active learning, the reform section had to demonstrate improvement in students’ quantitative problem-solving skills, as well as their conceptual understandings. Because many of the active-learning materials produced by physics education research (PER) focus on developing students’ conceptual understandings (e.g., Hieggelke et al., 2012; ), we had to adapt and develop active-learning approaches to help improve students’ abilities to solve quantitative problems. This paper describes all aspects of our reform effort: how we used active learning in novel ways to simultaneously promote quantitative problem-solving among 200-plus students in a large lecture setting, how we compared the performance of students in the traditional and reformed sections, and how the results of this study instigated a cultural change in the Department of Physics.
Note that this reform effort was not initially envisioned as a research experiment. Consequently, we did not control for every possible variation in the two sections that might contribute to differences in student performance (e.g., differences in the homework assignments of the two sections, as well as some differences in topic pacing and depth of coverage). However, by the end of the semester, it was clear that the dramatic improvements in students’ performance in the reformed section, over those of their peers in the traditional section, could be attributed to the in-class experiences afforded by the active-learning activities, rather than to some other variables that we did not control for.
This paper appears similar to the study of Deslauriers et al. (2011). In that study, a first-time physics instructor served as a guest instructor for a single week in a section of a physics course. The first-time instructor made heavy use of active-learning strategies. During the same week, an experienced instructor gave traditional lectures on the same content to students enrolled in a second section of the same course. Deslauriers et al. found that students taught by the first instructor outperformed their peers taught by the experienced instructor on 12 multiple-choice questions designed to measure students’ conceptual understandings.
Our study and course reform effort were significantly larger than and extend the work of Deslauriers et al. (2011). We developed a semester-long curriculum, spanning the full range of topics commonly taught in introductory mechanics. Additionally, our reform effort included the development of a novel way to use active-learning strategies to foster quantitative problem-solving in the large-lecture environment. Finally, our assessments of students included both conceptual questions and quantitative problems, whereas Deslauriers et al. only examined students’ conceptual understandings. This paper expands the knowledge base on how to successfully implement research-based active-learning instructional approaches to create sustainable course transformations.
Reform effort
Before describing the traditional and reformed sections in detail, we want to situate this study and reform effort in the campuswide AAU-funded STEM education reform effort that was already underway at the University of Arizona. A major thrust of this effort involved changing the culture and practices related to teaching in several STEM departments (Burd et al., 2016). Research shows that cultural change practices that simply make innovative curriculum materials available to faculty, or that invoke “top-down” policies and mandates are ineffective. Successful reform efforts must endeavor to be both supportive of and compatible with the local culture, and use practices that are explicitly aligned with or work to change stakeholder’s beliefs (Henderson et al., 2011). Furthermore, a long-term view must be part of the collective beliefs of the stakeholders, and so we set out to create a change that would persist well beyond the one semester of the study reported here. Consequently, this reform effort involved bringing multiple stakeholders together, including both instructors, the associate department head, the department’s director of undergraduate studies, and other experts in PER to the table. We refer to this group as the “reform team.”
The reform team held a series of meetings in the summer prior to the semester’s instruction in order to establish a common set of course norms, policies, and goals for both the control and reformed sections. Throughout the semester, this group met weekly to develop and review particular active-learning strategies, discuss the progress of both courses, ensure that both courses were covering the same material at roughly the same time (although there were some differences in topic pacing and coverage), and develop appropriate free-response exam questions that could assess students’ physics content knowledge, reasoning abilities and quantitative problem-solving skills.
Comparing and contrasting the traditional and reformed sections
The course at the heart of this experiment was the first semester of introductory, calculus-based physics. Two hundred and fifty-eight students enrolled in the traditional section and 217 enrolled in the reformed section. We made no effort to advertise the differences between the two sections while students were enrolling. The content of the course focused on traditional physics topics such as kinematics, Newton’s laws of motion, impulse and momentum, work and energy, rotational motion, gravitation, periodic motion, and fluids. The course is primarily taken by students pursuing degrees in the physical sciences and engineering.
There were no statistically significant differences between students in the traditional and reformed sections in terms of their SAT/ACT scores, scores on a math placement exam, Pell grant eligibility, and percentages of males versus females. There were also no statistically significant differences between the two sections in terms of the representation of different races and ethnicities among enrolled students. An independent samples t-test did reveal that students in the reformed section had a lower average high school GPA (3.58) than students in the traditional section (3.69) at a statistically significant level (p = 0.008) (McGrath, 2015).
Students from both the traditional and reformed sections attended a 170-minute laboratory session each week. We will not comment further on these labs, as they were identical between the traditional and reformed sections.
Students in the traditional section had three 50-minute lectures each week, whereas students in the reformed section only had two 50-minute lectures each week. The reformed section gave up a full 50-minute lecture each week so that students could attend a weekly small-group (N ≈ ٢٥) recitation section, which will be described in more detail in the next section. The presence of these recitations sections meant that while the reformed course had 50 fewer minutes in the lecture hall each week, the total amount of time students were expected to be in class was identical between the two sections. Because the exams for both sections occurred on the same day, both instructors had to make sure that they had covered the relevant content by that date— thus, the reformed section had to provide instruction on new content with two, rather than three, lectures a week.
No “studio” or “SCALE-UP” style rooms were available for either section. Instead, lectures for both sections were held in the same large lecture hall, with stadium-style seating and desks that were bolted to the ground. The lectures were held back-to-back in the morning.
We made sure that all graded elements of the course were weighted equally between the two sections. Homework accounted for 15% of their final course grade, laboratories accounted for 20%, the three midterms together constituted 40% of their final grade, and the final exam accounted for 25%. The common exams were all held in the evenings at the same time in order to eliminate the possibility that students from one section might divulge the content of the exam to students from the other section. Final letter grades were assigned to students from both sections based on the same scale. Both sections also used the same textbook (Young & Freedman, 2012). All of these details were agreed upon by the reform team before the semester began.
Active learning in the reformed section
Each instructor created his own content for the lectures and assigned his own homework problems. Because the reformed section only met for lecture twice a week, the first-time instructor did not devote a substantial amount of class time to reproducing complex derivations from the textbook, nor did he introduce mathematical formalism (e.g., vector calculus) at the start of the semester, instead opting to provide the relevant mathematics needed for the physics being studied on the day the topic was introduced (e.g., the dot product of two vectors was introduced when students began studying work). Rather than focusing class time on derivations of equations, the reformed section’s lectures focused on developing students’ conceptual understandings, reasoning abilities, quantitative problem-solving skills, and fluencies with multiple-representations of the discipline. To accomplish this, the first-time instructor made use of multiple research-validated and research-informed active-learning strategies, including Think-Pair-Share (aka “TPS” or “Peer Instruction”; Lyman, 1981; Mazur, 1997) and Ranking Tasks (RTs) (Hieggelke et al., 2012; O’Kuma et al., 2008). As previously noted, these instructional strategies are typically used to improve students’ conceptual understandings and reasoning abilities.
Before unpacking how the reformed section used active learning to also increase students’ quantitative problem-solving skills, consider how typical physics classes, including the traditional section, typically teach students how to problem solve. In a typical physics class, the instructor chooses a few problems that they use to model problem solving in front of students. Those students passively watch the instructor and take notes. Both the instructor and students hope that, through this process, students will learn how to interpret a problem, apply the relevant physics, develop a solution plan, and successfully execute the necessary calculations. Because students are not actively practicing these skills in class, both the instructor and students may not realize the degree to which students are struggling until after the homework or exams have been graded—and by then the course has moved on to new material.
Office hours are one place where faculty can gain an appreciation for students’ struggles and provide students with the help they need to learn the material. However, because students who attend are self-selected, this can easily misrepresent the primary difficulties of the class as a whole. Office hours are also an inefficient way to help a large number of students overcome whatever difficulties they are experiencing with the material. At the heart of our reform effort was the desire to bring the benefits of “office hours” to the large lecture classroom. Consequently, we re-conceptualized the use of “lecture time” during the reformed section. The active-learning model we created was designed to promote an “office hours experience” for the entire class at once in order to help them integrate their developing conceptual understandings with their emerging quantitative problem-solving abilities.
During each class, students in the reformed section were presented with a problem and given a few minutes to attempt a solution while working in collaboration with their neighbors (see the Appendix for an example problem). The first-time instructor carefully chose problems that would elicit multiple and well-understood problem-solving and conceptual difficulties. While students worked toward a solution, the instructor would roam the room and answer questions. This brief initial problem-solving phase was critical because it afforded students the opportunity to interpret the problem, organize their ideas, and reason about how their physics knowledge might be applied to reach a solution for the problem. This initial phase helped students become aware of where along the solution pathway they “felt stuck”—an essential component of the in-class problem-solving curriculum.
The next phase of the curriculum used the TPS questioning and voting strategy. In this second phase, students were asked to vote on multiple-choice questions designed to unpack their conceptual and reasoning difficulties associated with solving the particular quantitative problem on which they had just attempted a solution. What made our use of TPS unique was that the choices modelled incorrect mathematical expressions that highlighted fundamental errors and problem-solving difficulties common to our student population. The sequence of carefully crafted TPS questions focused students’ thinking on specific steps along the problem solution pathway and it instigated peer conversations about the particular mathematical or physics applications known to be problematic for students (see the Appendix for example TPS questions). This novel use of mathematical expressions for choices to TPS questions forced students in class to unpack their mental models and think critically about quantitative problem-solving, rather than simply spend their class time hurriedly copying down the solution being created by the instructor. Our use of TPS allowed the first-time instructor, by himself (no teaching assistants [TAs] were present in lecture), to simultaneously engage over 200 students in collaborative problem solving during each class, all without having to collect and grade any additional work, while also addressing all the content being presented in the traditional section. Students in the reformed section gained experience identifying and applying relevant physical principles, monitoring their own understandings, and actively focusing their mental efforts on difficult steps in the quantitative problem-solving processes that physicists hold in high regard. For more details on how to effectively implement TPS for quantitative problem-solving, see Wallace (2020).
The reformed section’s weekly recitation sessions focused on further developing students’ conceptual understandings and problem-solving skills, but did not introduce any new content. Each session had approximately 25 students and was led by a graduate TA. An undergraduate learning assistant (LA) (Otero et al., 2006) was also present to help facilitate student learning. During each recitation, students worked in collaborative groups of three to four to solve a single quantitative problem. They also worked through a tutorial or ranking task activity inspired by curricula developed by physics and astronomy education researchers (Hieggelke et al., 2012; ). Students received a nominal amount of participation credit, which was incorporated into their homework grade, for their recitation work. The TAs and LAs were trained by the first-time instructor during weekly meetings. During these training meetings, they reviewed the coming week’s activities and engaged in a version of situated apprenticeship (Prather & Brissenden, 2009) in which they modelled authentic student difficulties and practiced using Socratic-style questioning techniques to help each other overcome those difficulties.
Findings
The big question of this reform effort was whether the focus of class time on collaborative group quantitative problem solving, driven by TPS questions, combined with the implementation of the weekly recitation section, would be enough to help students develop greater conceptual understandings and significantly improve their quantitative problem-solving skills as compared to their peers in the traditional section. To answer this question, we compared the performance of students in the two sections on the four common exams they took over the course of the semester.
The exams were created by the reform team well in advance of the instruction students in either course received on the relevant physics. The exams used both conceptual and quantitative free-response questions. One-third of the questions on each exam were conceptual and the remaining two-thirds were quantitative. The majority of the conceptual questions were derived from questions used in and validated by PER, such as the passing twice speed comparison task (Trowbridge & McDermott, 1980), the work-energy and impulse-momentum tasks (Lawson & McDermott, 1987; Pride et al., 1998), and the five blocks problem (Heron, 2004). The quantitative questions were chosen by the reform team to have a level of difficulty comparable to questions used in previous versions of the course. This allowed us to align our assessment practices with the cultural expectations of the department, which was important for leveraging any successes of the reformed sections toward the larger culture-change efforts.
All exam questions were graded by graduate TAs assigned to the traditional and reformed sections. The instructors from both sections collaborated to develop grading rubrics for the TAs to follow, trained the TAs on how to apply the rubrics, and periodically spot-checked graded exams to make sure that each question was being scored appropriately. The instructors also assigned a single question to a single TA, who then graded the responses of all the students in both sections to that question. This ensured that students in both sections were graded on the same scale and by the same person.
Because the classes differed with respect to the depth to which they covered certain topics, it is possible that students in one section may have done better on a particular exam item because they received more instruction on that topic and/or they saw a similar question during instruction. To investigate this possibility, one member of the reform team (not one of the section instructors) went through both sections’ lecture slides and homework (and, in the case of the reformed section, recitation activities) and compared each class’s content to the exam questions. He flagged all items that could have been biased toward one class or the other and then shared these results with the rest of the reform team to discuss. After discussion, we decided to keep items that use standard representations of the discipline (e.g., representing vectors with arrows), present contexts frequently encountered in introductory physics classes and textbooks (e.g., constant acceleration and projectile motion problems), and require quantitative procedures that are always taught in introductory physics (e.g., using conservation principles to solve 2D inelastic collision problems). We removed items from our analysis whose representations, contexts, or quantitative procedures went beyond what is described in the previous sentence.
Table 1 shows students’ average percent correct for both sections on every exam item, with biased items shaded. The listed uncertainties represent the standard deviation of the mean. Table 1 also shows, for each item, the difference (Δ) between the average score of the reformed section and the traditional section. Positive values (which are italicized, bolded, and in blue) indicate that the reformed section had the higher average score, while negative values (which are bolded and in red) indicate that the traditional section had the higher average score. Only item 1 on exam 3 had a Δ indistinguishable from 0, so it is not bolded, italicized, or colored.
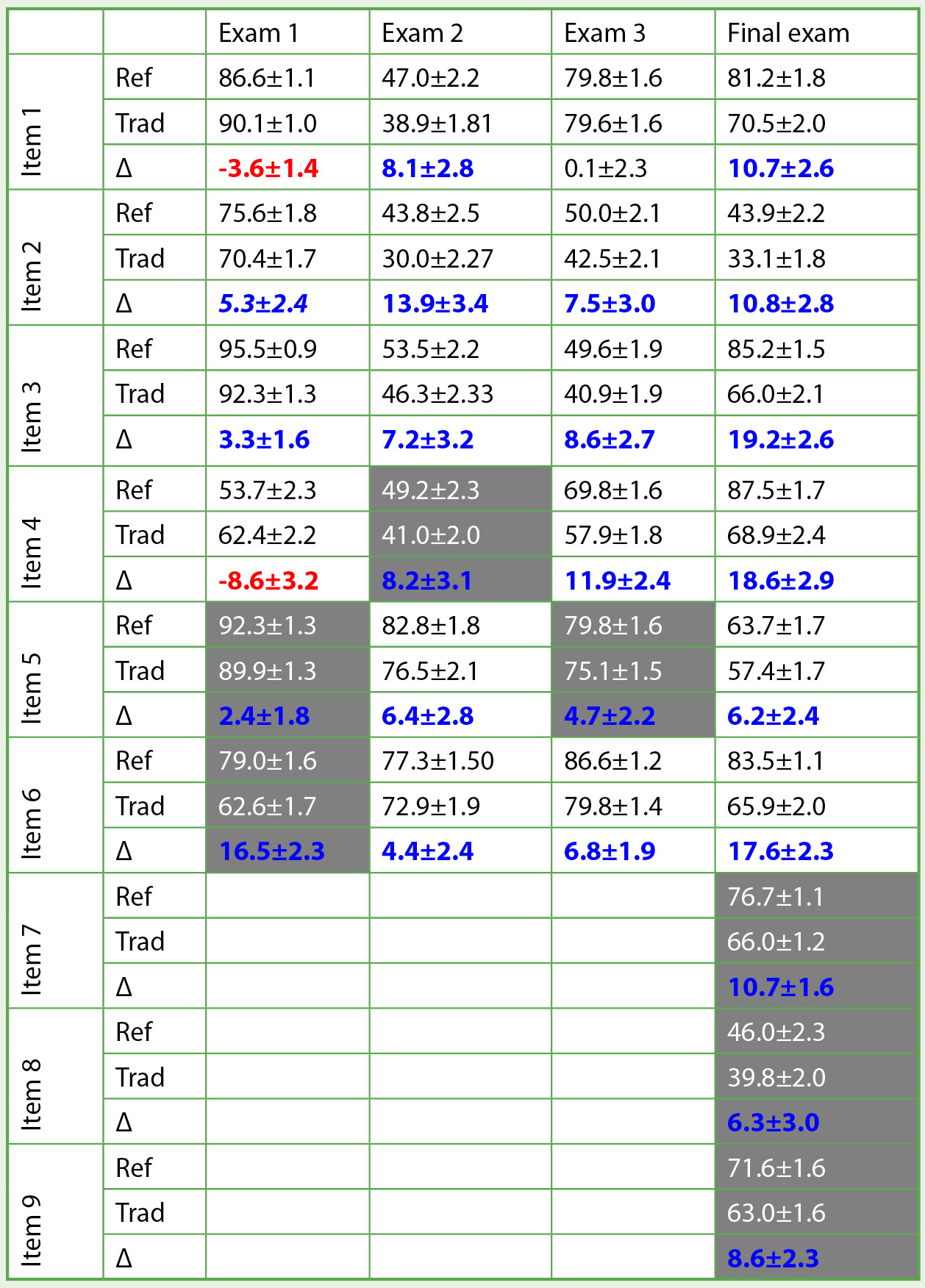
The average score of students in the reformed and traditional sections on every exam item. The Δ represents the difference between the average for the reformed section and the average for the traditional section; positive values (which are the color blue) indicated the reformed section had a higher average while negative values (which are the color red) indicate the traditional section did better. Errors represent the standard deviation of the mean. Items in dark grey boxes were flagged as biased toward the reformed section.
While in principle a question could have been biased in favor of either class, all the questions highlighted in Table 1 were biased in favor of the reformed class. This may be due to the fact that significant scaffolding and active engagement instruction is necessary for students to develop robust, physically correct understandings that enable them to successfully answer these questions. We should note that the reformed section did spend more time unpacking the contexts, representations, and problem-solving procedures used on many of the flagged items. This was done intentionally. Many students in introductory physics are novices at the subject when they begin the course. To help them become more expert-like requires explicit mentoring and modelling of the abilities and practices that represent discipline expertise. These abilities and practices should be decided upon in advance and exemplified in the instruction and assessments provided to students (Wiggins & McTighe, 2005).
For an example of an item that is biased, consider item 4 on exam 2. This item comes from the famous work-energy and impulse-momentum tasks designed by the University of Washington’s PER group (Lawson & McDermott, 1987; Pride et al., 1998). Students in the reformed section, unlike the traditional section, received explicit instruction on when to apply the work-energy theorem and when to apply the impulse-momentum theorem, and this instruction was reinforced in parts of two recitation activities.
Even if we ignore all items flagged as biased toward the reformed section, the reformed section had higher average scores on almost every question, with only two exceptions (items 1 and 4 on exam 1). The reformed class outperformed the traditional class on all other items on all exams, and in many cases the differences in scores were large (e.g., the difference on item 4 on the final exam was 18.6% ± 2.9%).
Figure 1 shows the average scores of each class on each exam. Note that we removed all items flagged as biased toward the reformed section when calculating these averages. The error bars represent the standard deviation of the mean.
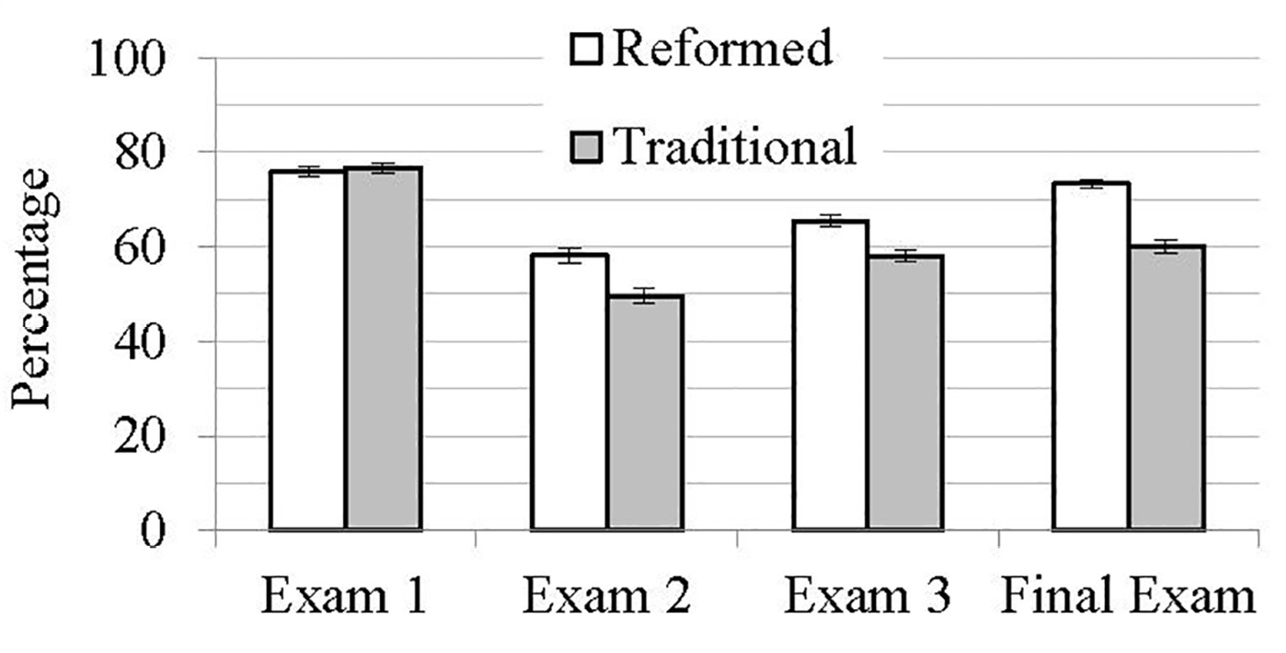
Average exam scores for both the traditional and reformed sections. Questions flagged as biased toward the reformed section were removed from the data set before calculating these averages. Error bars represent the standard deviation of the mean.
Note that the two sections performed roughly the same on the first midterm, and both sections did quite well. This result is not surprising because the content of the first exam covered topics many students studied in high school (kinematics and Newton’s laws of motion). However, the second exam was significantly more difficult as it addressed work-energy and impulse-momentum principles, with which many students have less experience. On the second exam, students in the reformed section outperformed students from the traditional section, with scores that were approximately 5–14% greater than the scores of their peers in the traditional section. This result held regardless of the question type (conceptual or quantitative). This same trend is present on the third exam and the final exam. What is especially noteworthy about the final exam is the magnitude of the item differences. On some items, students from the reformed section outperformed their peers in the traditional section by almost 20%. Notice that the average scores on exams 2 and 3 for the reformed section were higher than those of the traditional section (by 8.5% and 7.5%, respectively). On the final exam, the difference between the sections was 13.2% in favor of the reformed section. Because the final exam was a cumulative exam, this result suggests that the effects of active learning may be cumulative: As students spend more time actively engaging with the material, they experience increased abilities to recall, apply, and synthesize what they have learned, even in contexts that are prima facie novel.
Conclusions
We conclude that students in the reformed section, taught by a first-time instructor using active-learning teaching strategies, outperformed their peers in the traditional section, which was taught by a highly regarded and very popular traditional instructor whose instruction relied primarily on lecture. This result is quite robust because it is virtually insensitive to which exam items are included or excluded from the analysis. The results of this study strongly suggest that the use of active-learning teaching strategies, including collaborative problem-solving in the large-lecture environment, is more effective at supporting student learning of physics—even when the course is taught by a first-time instructor.
The reform effort described in this paper was also successful in affecting a cultural change in the University of Arizona’s Department of Physics. Since this experiment was run, the department has transitioned to making the recitation sections a permanent feature of all their introductory courses. They have also continued to develop, adapt, and adopt curricula and instructional techniques that are informed by the results of discipline-based education research in general and PER in particular. Numerous departmental stakeholders, including, but not limited to, members of the reform team, have successfully pushed to increase the use of active-learning pedagogical techniques in other courses offered by the department. The recitation materials the department is using in the calculus-based mechanics course discussed in this paper and the materials in all of their other courses are all available online (see University of Arizona, 2021). The broader reform efforts of the department have been galvanized by our implementation of TPS for interactive problem solving, which has been shown to be easy to use and highly successful at increasing students’ physics knowledge. We hope this reform model will inspire other instructors at other institutions to transform their courses to help their students. ■
Acknowledgments
We thank Shelley McGrath for her work as the external evaluator for this project. This work was supported by the American Association of University’s Undergraduate STEM Education Initiative.
Appendix
Colin S. Wallace (cswphys@email.unc.edu) is a teaching associate professor in the Department of Physics and Astronomy at the University of North Carolina at Chapel Hill in Chapel Hill, North Carolina. Edward E. Prather is a professor of astronomy at the Center for Astronomy Education, Steward Observatory at the University of Arizona in Tucson, Arizona. John A. Milsom is an associate professor of practice, Ken Johns is a professor and associate department head, and Srin Manne is an associate professor, all in the Department of Physics at the University of Arizona in Tucson, Arizona.
Assessment Curriculum Teaching Strategies Postsecondary


