special issue
Using Multiple Models to Learn about COVID-19
The Science Teacher—January/February 2023 (Volume 90, Issue 3)
By Jamie Elsner, Troy Sadler, Eric Kirk, Rebecca Rawson, Patricia Friedrichsen, and Li Ke
As COVID-19 spread rapidly throughout the world, teachers had the difficult challenge of developing curricular materials on and teaching about viral pandemics with minimal resources. At the same time, students were concerned about contracting the virus and expressed interest in learning about topics such as how COVID-19 came to be and how to prevent it (Elsner et al. 2022). Science classrooms are well suited to address students’ questions and concerns about the pandemic through scientific exploration of viruses. If students are to be responsible global citizens, they must understand the mechanisms of viral transmission to make informed health decisions and contribute to the well-being of their communities. In addition, high school students’ health practices directly affect their lives since these practices relate to reopening schools, seeing friends, and returning to work.
Without obvious links between topics of infectious disease (e.g., prevention strategies, infection curves, reproduction rates) and traditional curricular themes, teachers may wonder how instruction on viral pandemics fits with the Next Generation Science Standards (NGSS). We found it difficult to make connections between NGSS disciplinary core ideas and scientific ideas important for understanding viruses and pandemics. However, living through a global pandemic made it painfully clear that concepts associated with viruses—including transmission, viral spread in communities, immune responses, and vaccine mechanisms—represent important science content that would be helpful for students to understand. Also, other dimensions of the NGSS (beyond DCI), including both crosscutting concepts and science and engineering practices, were useful in supporting student learning about the pandemic. We found the NGSS practice of developing and using models to be a particularly valuable approach for helping students negotiate the complex scientific issues of COVID-19. This article describes three different types of models that address the pandemic from multiple perspectives to help students learn how to slow the spread of COVID-19.
Why use modeling?
Models are tools such as drawings, diagrams, physical objects, mathematical algorithms, diagrams, or computer simulations (Lehrer and Schauble 2006). They are often simplified representations of complex systems that can be used as instructional resources and supports for complex reasoning. Students can engage with models in various ways, including model creation, testing, revision, and evaluation. Students can also use models to build explanations or make predictions. Through manipulating models, students inherently apply knowledge and construct new knowledge (Nersessian 2008) and, importantly, take ownership of their learning as they make choices for their models.
In the context of COVID-19, there are many social dimensions at play (e.g., politics, economics, personal health practices) that influence disease outbreak in addition to biological components of the pandemic (e.g., viral transmission, mutations, human disease symptoms). Furthermore, multiple scientific disciplines, such as immunology, genetics, epidemiology, and microbiology, contribute to our understanding of the pandemic. Thus, COVID-19 is a complex socioscientific issue (SSI), meaning that science concepts related to the virus have real-world implications for problems in society (Zeidler 2014). SSIs do not have straightforward solutions—scientific evidence can and should be used to inform decision making and solution seeking to these issues; however, science alone can rarely provide solutions that meet the needs of everyone involved with the issue. SSI-based teaching and learning creates opportunities for students to grapple with real-world problems relevant to their own lives and that require consideration and evaluation of multiple, sometimes competing, factors associated with the issue. This can help students become more adept at analyzing problems from multiple perspectives, looking for different forms of evidence, and thinking critically. Student engagement with models can be a helpful tool to support these kinds of outcomes, and given the complexity of an SSI like a global pandemic, multiple models that address different dimensions of the issue can be particularly useful (Ke et al. 2021).
In response to the challenges and opportunities presented by the pandemic, we worked with a group of high school teachers to develop and implement SSI-based modeling activities for students around COVID-19 (Sadler et al. 2020). Here we present three different types of models that address the pandemic from multiple perspectives and tackle the focal issue: How do we slow the spread of COVID-19? This series of modeling activities allowed students to represent and explain different features of the pandemic with the goal of students coordinating ideas across topics and models. Using multiple models is one of the objectives envisioned in the NGSS learning progression for modeling. By grade 12, students should be able to “move flexibly between model types when different ones are most useful for different purposes” (National Research Council 2012, p. 58). In addition, multiple modeling experiences can help students develop stronger ideas about the practice of modeling—when to use models, purposes of models, and benefits and limitations of models (Ke et al. 2021). In the following sections, we present a brief overview of three modeling experiences we developed and implemented during the 2020-2021 school year. The modeling activities were embedded in a broader unit designed for high school biology classes; descriptions of the full unit and the individual modeling activities can be accessed online at https://epiclearning.web.unc.edu/covid (Sadler et al. 2021).
Activity 1: Handwashing descriptive and mechanistic model
Teachers began this activity by asking students, “Why is handwashing important?” and “Why is washing your hands for 20 seconds with ordinary soap an effective way of combating COVID-19?” Students were definitely aware of widespread calls for handwashing, but very few students knew much about why soap is effective against the spread of coronaviruses. Based on the students’ limited knowledge, we chose to show an informational video (“How soap absolutely annihilates the coronavirus”; Resnick 2020) that highlights the effects of soap on the coronavirus. The video explains how the properties of soap molecules make it effective at limiting the spread of viruses. Some teachers may want to engage students in initial model creation before students view information resources (like the video we shared) or do other activities designed to introduce content. We chose to show the video first because our formative assessments had suggested a limited knowledge base, which can lead to less-than-productive initial modeling experiences.
After watching the video, students created two types of models: a descriptive model (Figure 1A) and a mechanistic model (Figure 1B). In the descriptive model, students identified key structures of soap molecules (i.e., hydrophilic head and hydrophobic tail) and COVID-19 (i.e., protein, fatty envelope, and genetic material), which they later used as part of their mechanistic models. Descriptive models are valuable for describing features in a system and how they relate to one another. Teachers further probed students’ understanding of viral properties by asking questions such as

Descriptive and mechanistic models of handwashing.
- How is a virus protected from plain water?
- What part of a virus keeps it from being washed away by plain water? What property of this structure allows it to cling to skin?
To expand on their descriptive models, students created a mechanistic model to show how the structures of a soap molecule help oil mix with water, a key concept for understanding why handwashing is effective at eliminating viruses (Figure 1B). Mechanistic models are useful for building knowledge because they create opportunities for students to represent what they understand and to formalize aspects of that understanding. In addition, these models highlight underlying phenomena that may not be obvious to students and how they apply to other situations (e.g., why soap works to destroy other viruses, not only COVID-19). As in this activity, mechanistic models can also be leveraged to help students relate structure and function, one of the seven NGSS crosscutting concepts. For example, students demonstrate how the molecular properties of soap work to trap oils. This serves the function of lifting viruses off the skin and into the drain when you wash your hands in water.
The ways in which students represent their ideas may look different. For instance, some students used before and after drawings to demonstrate sequences over time, whereas others added explanations to describe processes like in the example provided in Figure 1B. Teachers can also ask students to compare and contrast their models with peers, encouraging students to evaluate one another’s models and make revisions to their own models. Models are more than end products that students create; they are beneficial sensemaking tools that students can use to support their explanations. To elicit further explanation, we asked students to use their models as evidence to answer other questions such as
- What happens when soap comes in contact with a virus such as the coronavirus?
- Why should you wash your hands for at least 20 seconds?
- What advantages does soap have over hand sanitizer?
Activity 2: Infection curve computer simulation
During the COVID-19 pandemic, social distancing became an important strategy for preventing viral spread. The second modeling experience helped students explore the science behind this strategy by engaging in mathematics and computational thinking. For this aspect of the work, we chose a Netlogo computer simulation (www.jacobkelter.com/infection-model) that allowed students to identify patterns and make sense of underlying cause-and-effect relationships associated with social distancing—two of the NGSS crosscutting concepts. Netlogo is an agent-based computer modeling platform that enables users to manipulate simulations of a wide range of phenomena (Wilensky 1999). In the model we used, students manipulated variables such as population density and percent distancing (i.e., the percent of time spent at home versus in public) to determine their effects on infection rates (Kelter 2020).
We also had students use the model to explore how these factors affected infection rates and to make predictions about different social distancing conditions (e.g., What level of distancing is required to decrease the infection rate by half in a dense population?). As shown in a screenshot from the modeling interface in Figure 2, the model displays simulation results in the form of an infection curve. Our partner teachers used this to initiate discussions around what it means to “flatten the curve” and make connections to how scientists might use similar models to make predictions of hospitalization rates and the availability of ICU beds. We also asked students to consider limitations of the model. Students need to be aware that no single model perfectly represents a larger system. For instance, some variables not included in this simulation—such as wearing masks—can significantly influence infection rates.
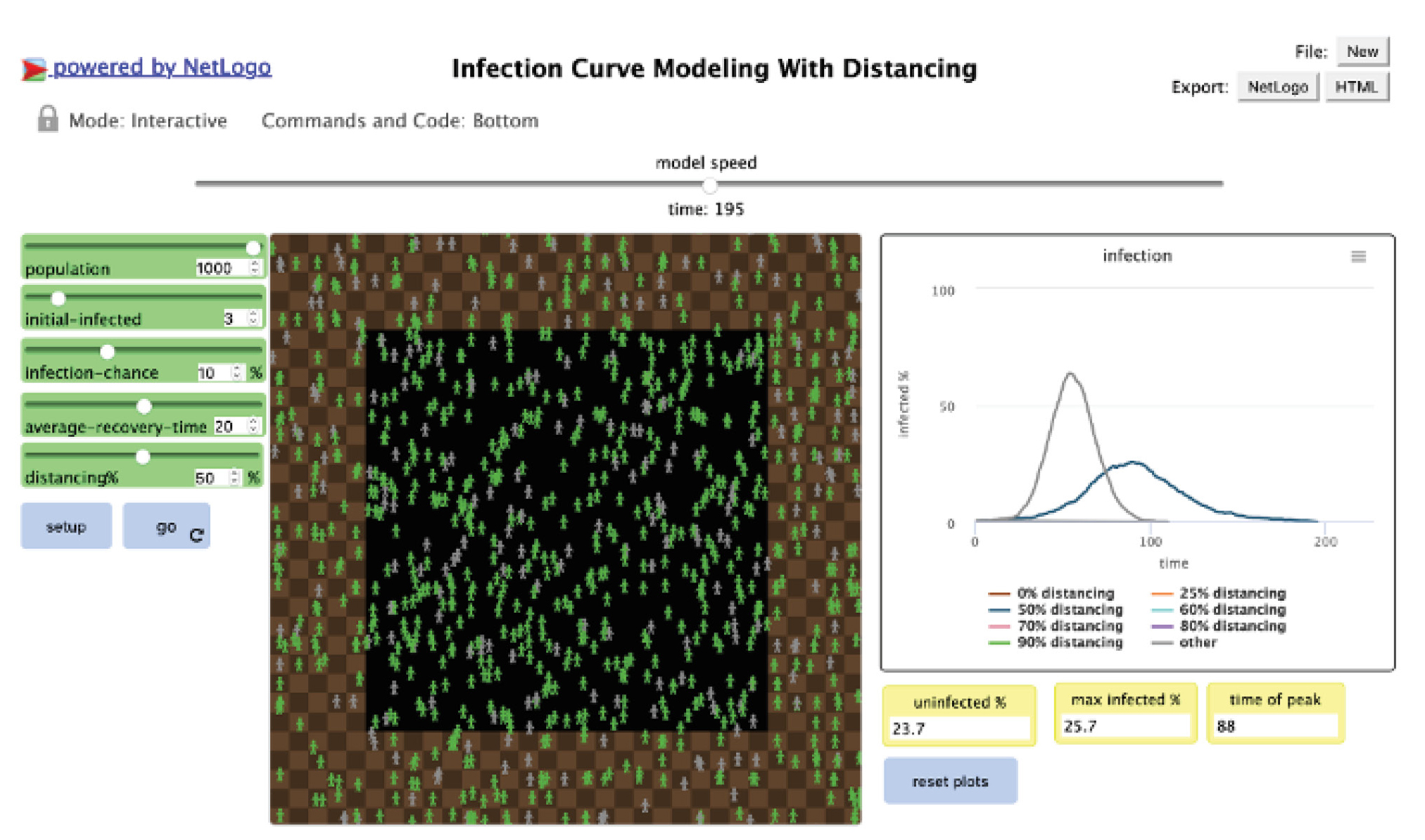
Infection curve computer simulation.
Activity 3: Viral spread mathematical model
Once students had a basis for interpreting infection curves, we introduced a third model to help students better understand why COVID-19 spread so quickly. This mathematical modeling experience introduced concepts of exponential growth and reproduction rates (R0), which relate to the NGSS crosscutting concept of stability and change. For this modeling tool, we programmed a spreadsheet that enabled students to compare viruses with different reproduction rates (e.g., the common flu) and visualize viral transmission numerically and graphically. This mathematical model presents a simplified case of viral spread because it does not account for recovery rates or population density. However, the advantage of the simplified representation is that it helped students recognize the basics of exponential growth, which is often nonintuitive. As the pandemic continued, this modeling task became helpful for comparing different COVID-19 variants and contagiousness, incorporating the NGSS crosscutting concept of scale, proportion, and quantity. Teachers guided students through the modeling activity with several questions designed to help students understand the implications of viral spread and conditions that might affect communicability:
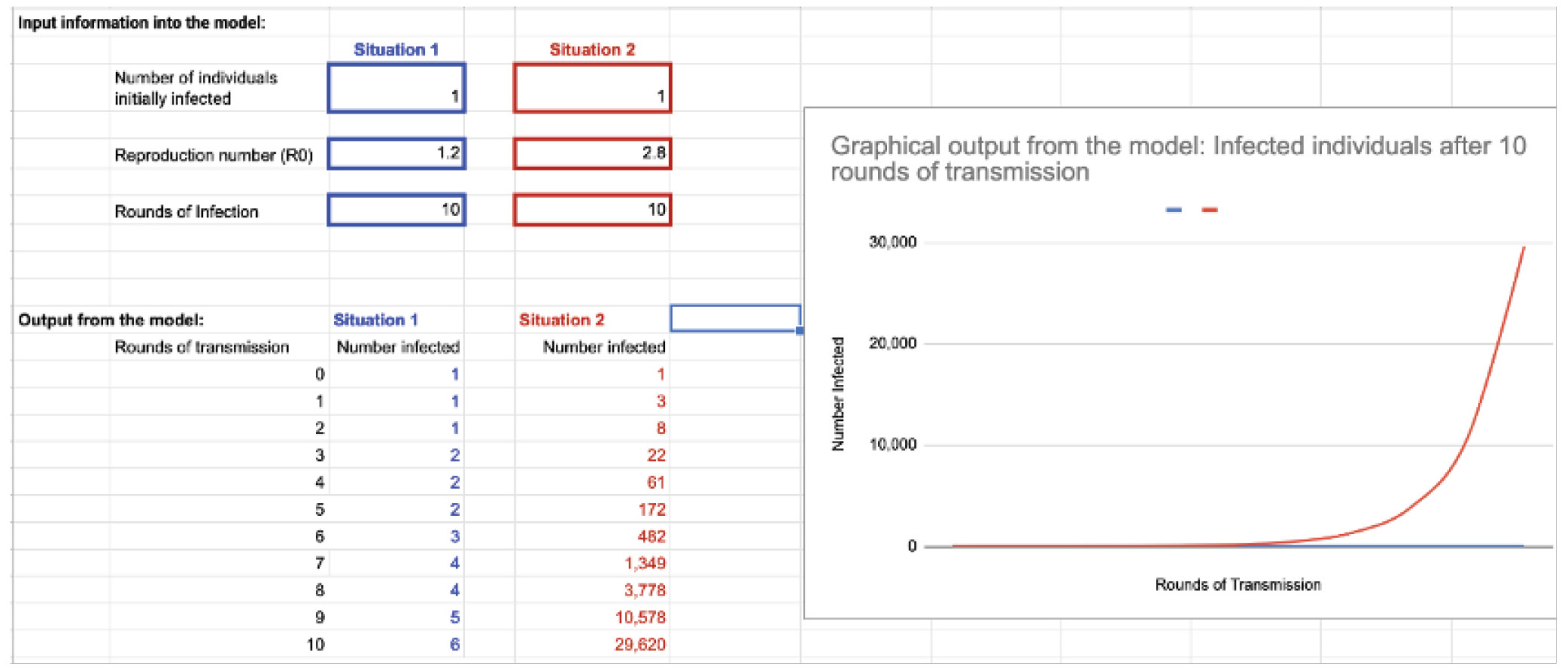
Viral spread mathematical model.
- What factors might contribute to the low rate of viral transmission of the flu compared to COVID-19?
- What happens to a viral outbreak when R0 for the virus falls below 1?
- What things could be done to lower the COVID-19 R0?
- If we assume that 100,000 individuals are infected by COVID-19, but we were able to drive its R0 down to 0.2, how long (in rounds of transmission) would it take to halt the spread of the virus?
Making connections across models
As students worked through the three models, they drew connections between and across the models. For instance, knowledge about how handwashing works at a molecular level to reduce viral spread helped students understand how R0, featured in the mathematical model, could be reduced. The handwashing model also helped students understand a limitation of the infection curve simulation, which did not account for prevention strategies other than social distancing. In another case, student experimentation with the mathematical model informed their understanding of the infection curve produced in the Netlogo simulation.
One of our goals in presenting multiple models was for students to identify the affordances and limitations of different models and generate high-quality scientific explanations by integrating evidence from multiple models (Georgen and Manz 2021). However, we found that students often struggled to make these connections and saw models as single entities. To support student sensemaking across the models, we created a series of common questions designed to direct student attention to potential connections and how those connections illuminate important science concepts. These guiding questions are presented in Figure 4. Teachers can use these questions to support student discussion around the similarities and differences between the three model types and what each of the models show us that others do not. Our goal is to help students evaluate different aspects of COVID-19 and identify how the various science concepts are related.
Guiding questions for multiple models
Underlying features:
- What does [feature of model] represent?
- Example from model 2: What does “distancing%” represent?
- How does the model relate to [science concept]?
- Example from model 1: How does handwashing relate to molecular interactions?
- What information did you gather from your model that helps us answer the driving question?
- What is the model not able to show us?
Comparing multiple models:
- What similarities/differences do you notice between [model 1] and [model 2]?
- What does [model 1] show us that [model 2] does not?
- What information does [model 1] give us that we need to understand [model 2]?
- Why do we need both [model 1] and [model 2] to answer the [driving question]?
Sentence starters for multiple models:
- Model 1 and model 2 both relate to [science concept] because __________, but model 1 shows us ________ and model 2 shows us __________.
- [Model 1] showed us ______ that we used for _______ in [model 2].
- [Model 1] showed us ______, which was the same/different as [model 2] because ___________.
Assessment
We see these modeling activities being useful as formative assessments. For example, the probing questions presented in Figure 1B can be used to assess student understanding of handwashing. Not everything a student knows about a topic will be represented in their models. Therefore, we encourage teachers to ask follow-up questions to monitor student understanding. The three modeling activities presented here are part of a larger unit that ended with a culminating activity in which students developed three policy recommendations to reduce the spread of COVID-19 in their city or town. A key aspect of this activity was that students had to use at least one model in their rationale and explain why that model supported the policy they were advocating. This allowed teachers to evaluate students’ explanation and application of their selected model.
Conclusion
In response to the emerging pandemic, we collaborated with high school science teachers to create modeling experiences that featured different kinds of models: a descriptive model linked with a mechanistic model, a computational simulation model, and a mathematical model. By engaging with these models, students developed understandings of the science behind prevention strategies and why these strategies work to reduce the spread of COVID-19. Additionally, the activities provided students with experiences working with multiple models that inform everyday health decisionmaking and relate to larger social factors that affect students’ lives. Although these models were demonstrated within the context of COVID-19, they can serve as useful examples of how multiple models can be leveraged in science classrooms in response to other pandemics as well as other socioscientific issues.
Acknowledgment
This research was supported by the National Science Foundation under grant DRL-2023088. The ideas expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
Jamie Elsner (jelsner@unc.edu) is a doctoral student, Troy Sadler (tsadler@unc.edu) is a professor, Eric Kirk (eric.kirk@unc.edu) is a doctoral student, and Rebecca Rawson (rrawson@email.unc.edu) is a doctoral student at the University of North Carolina at Chapel Hill, School of Education, Chapel Hill, NC. Patricia Friedrichsen (friedrichsenp@missouri.edu) is a professor at the University of Missouri, College of Education and Human Development, Columbia, MO. Li Ke (lke@unr.edu) is an assistant professor at the University of Nevada, Reno, College of Education and Human Development, Reno, NV.
Crosscutting Concepts Curriculum General Science Instructional Materials Lesson Plans Mathematics NGSS Policy Science and Engineering Practices Teaching Strategies Technology High School


